无监督学习-聚类算法

1、聚类介绍

1.1、聚类作用

• 知识发现
• 异常值检测
• 特征提取 数据压缩的例子

  ---

  1.2、有监督与无监督学习

  有监督：

  • 给定训练集X和标签Y
  • 选择模型
    • 学习（目标函数的最优化）
    • 生成模型（本质上是一组参数、方程）

      根据生成的一组参数进行预测分类任务

      无监督：

      • 拿到的数据只有X没有标签，只能根据X的相似程度做一些事情
      • Clustering 聚类：
        • 对于大量未标注的数据集，按照内在的相似性来分为多个类别（簇）目标：类别内相似度大，类别内相似度大，类别间相似小
        • 也可以用来改变数据的维度，可以将聚类结果作为一个维度添加到训练数据中。
        • 降维算法，数据特征变少

          1.3 聚类算法

          

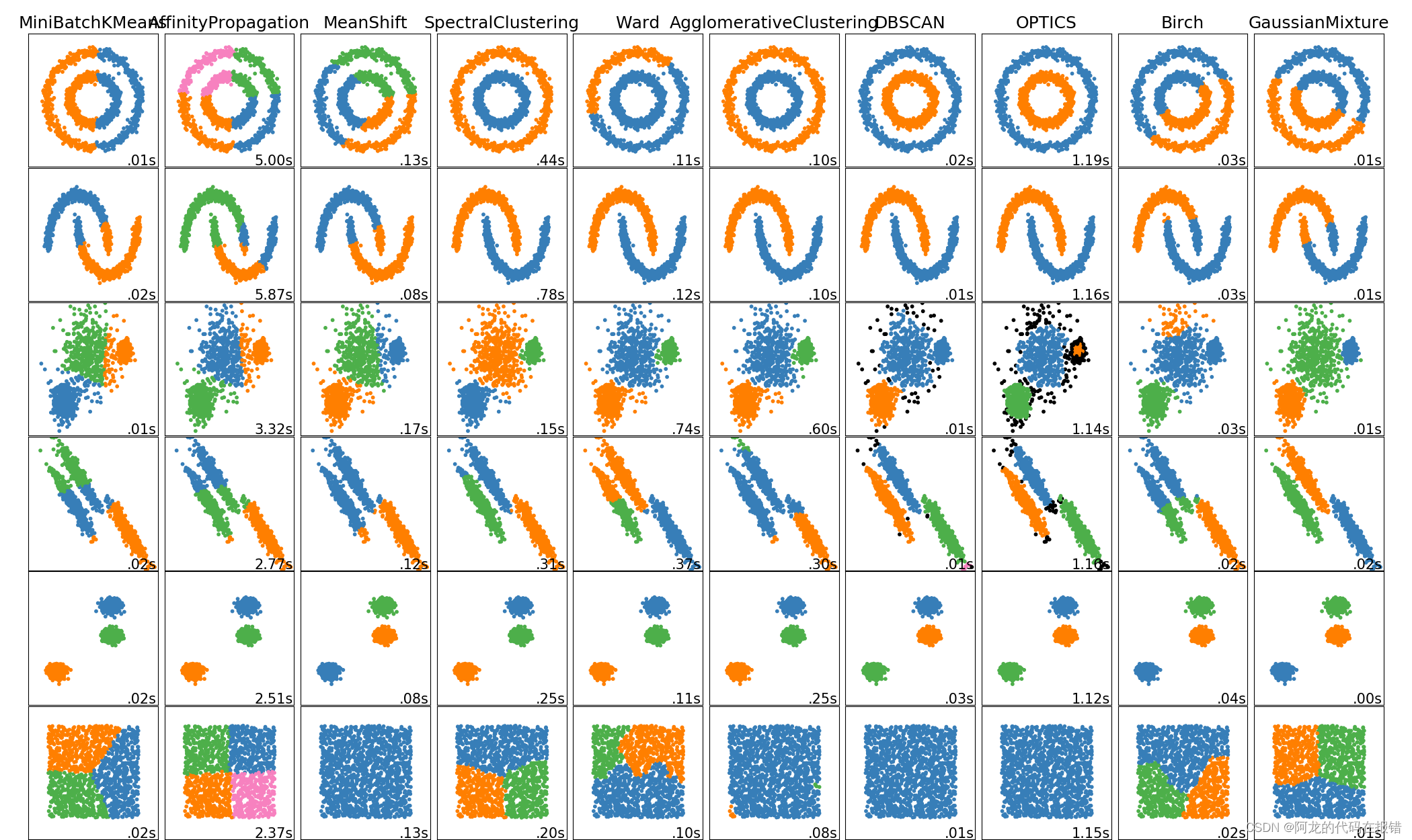
          图片来源：https://scikit-learn.org.cn/view/108.html

          ---

          1.4 数据间的相似度

          • 每一条数据都可以理解为多维空间中的一个点。
          • 可以根据点和点之间的距离来评价数据间的相似度

            ---

            1.5 余弦距离

            将数据看做空间的中的点的时候，评价远近可以用欧式距离或者是余弦距离

            计算过程如下：

            • 将数据映射为高维空间中的点（向量）
            • 计算向量间的余弦值
            • 取值范围[-1,+1]趋于近于1代表相似，越趋于-1代表方向相反，0代表正交

              c o s θ = a ⋅ b ∣ ∣ a ∣ ∣ 2 ∣ ∣ b ∣ ∣ 2 cos\theta = \frac{a \cdot b}{||a||_2||b||_2} cosθ=∣∣a∣∣2​∣∣b∣∣2​a⋅b​

              c o s θ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 × x 2 2 + y 2 2 cos\theta = \frac{x_1x_2 + y_1y_2}{\sqrt{x_1^2 + y_1^2} \times \sqrt{x_2^2 + y_2^2}} cosθ=x12​+y12​ ​×x22​+y22​ ​x1​x2​+y1​y2​​

              • 余弦相似度可以评价文章的相似度，从而实现对文章，进行分类。

                ---

                K-means

                2.1 聚类原理

                • 将N个样本映射到k个簇中
                • 将每个簇至少有一个样本

                  基本思路：

                • 先给定k个划分，迭代样本与簇的隶属关系，每次都比前一次好一些
                • 迭代若干次就能得到比较好的结果

                  2.2 K-means 算法原理

                  算法步骤：

                  • 选择k个初始的簇中心
                  • 逐个计算每个样本到簇中心的距离，将样本归属到距离最小的那个簇中心的簇中
                  • 每个簇内部计算平均值，更新簇中心
                  • 开始迭代

                    

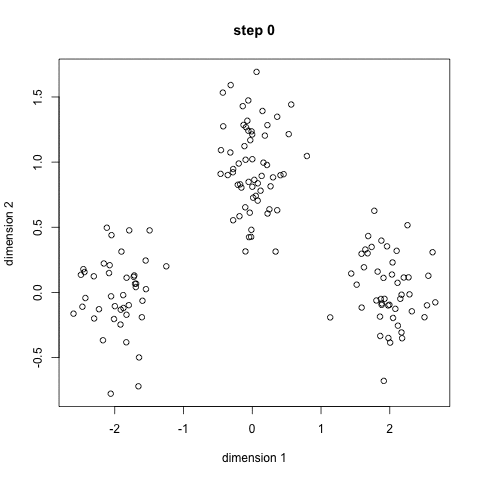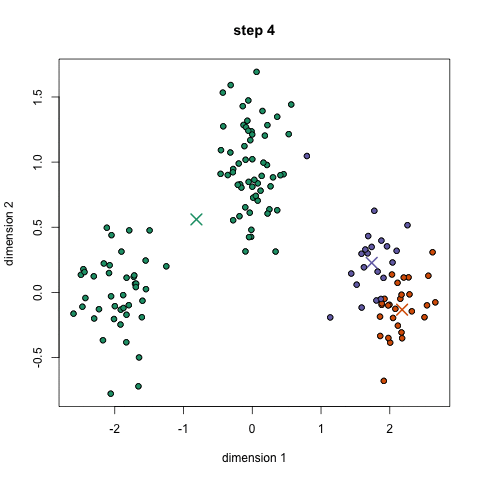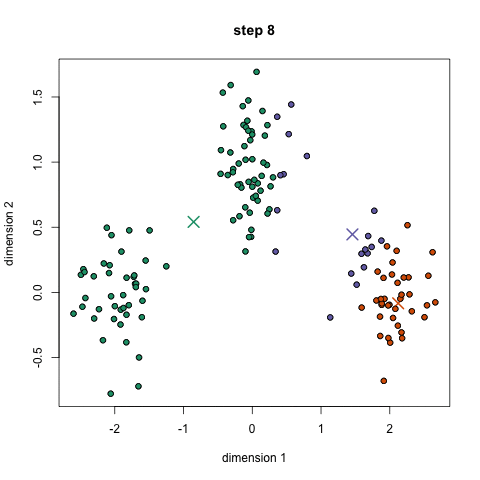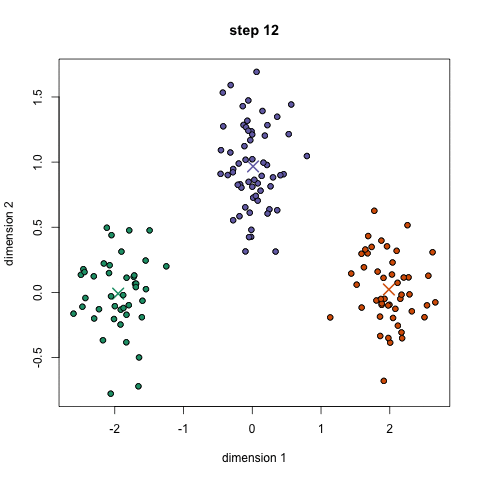
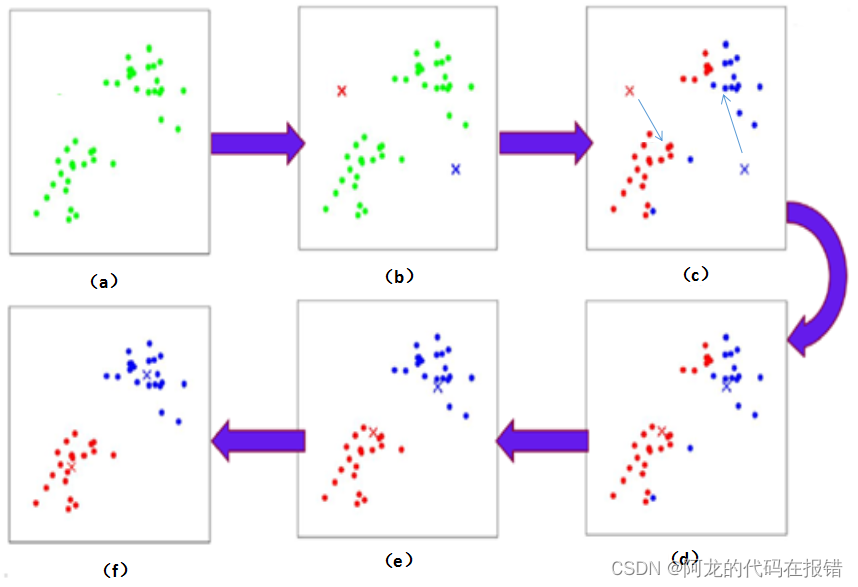
                    聚类的过程：

                    

                    2.4 k-means 损失函数

                    ∑ i = 0 n min ⁡ μ j ∈ C ( ∣ ∣ x i − μ j ∣ ∣ 2 ) \sum\limits_{i=0}^{n}\underset{\mu_j \in C}\min(||x_i - \mu_j||^2) i=0∑n​μj​∈Cmin​(∣∣xi​−μj​∣∣2)

                    • 其中 μ j = 1 ∣ C j ∣ ∑ x ∈ C j x \mu_j = \frac{1}{|C_j|}\sum\limits_{x \in C_j}x μj​=∣Cj​∣1​x∈Cj​∑​x 是簇的均值向量，或者说是质心。

                    • 其中 ∣ ∣ x i − μ j ∣ ∣ 2 ||x_i - \mu_j||^2 ∣∣xi​−μj​∣∣2代表每个样本点到均值点的距离（其实也是范数）。

                      2.5 K-means 执行过程

                      

                      愿君前程似锦，未来可期去💯,感谢您的阅读，如果对您有用希望您留下宝贵的点赞和收藏

                      本文章为本人学习笔记，如有请侵权联系，本人会立即删除侵权文章。可以一起学习共同进步谢谢，如有请侵权联系，本人会立即删除侵权文章。

                       
                       东莞企业网站建设  企业网站搭建公司  上海网站排名seo公司  成都网站建设seo  小程序开发流程详细  开网络公司