- nginx Rewrite
- plsql developer 一键格式化sql美化sql
- SpringMVC基础篇(二)
- 如何下载IDEA2023.3.4 最新激活破解教程
- springboot与tomcat关系
- .Net4.0 Web.config 配置实践
- Golang流程控制语句
- 【MySQL精炼宝库】数据库的约束 | 表的设计 | 聚合查询 | 联
- k8s中,kubelet 出现问题, k8s-master node
- 【微服务】配置Nacos管理SpringBoot配置文件(附解压包)
- Spring IoC&DI(3)
- springboot + vue 前后端加密传输 RSA互相加解密、加
- 探索设计模式的魅力:开启智慧之旅,AI与机器学习驱动的微服务设计模式探
- workstation 用途
- Java面试八股文(JVM篇)(❤❤)
- Vue3 + Django 前后端分离项目实现密码认证登录
- 21、Lua 面向对象
- [架构之路-214]- UML-类图图解、详解、结构化、本质化讲解
- 前端 Vue启动本地(.exe)文件
- SpringBoot(java)实现websocket实现实时通信
- 已解决com.mysql.cj.jdbc.exceptions.Com
- IDEA启动Springboot报错:无效的目标发行版:17 的解决办
- 【解决】Spring Boot创建项目常见问题
- 【Docker系列】在 Linux 上安装 Docker Compos
- 爬虫解析——Xpath的安装及使用(五)
- xcode c++项目设置运行时参数
- Spring容器结构
- 自动化机器学习流水线:基于Spring Boot与AI机器学习技术的融
- 前端Vue日常工作中--Watch数据监听
- Matlab方程组拟合【案例源码+视频教程】
基本概念
A*算法最早于1964年在IEEE Transactions on Systems Science and Cybernetics中的论文《A Formal Basis for the Heuristic Determination of Minimum Cost Paths》中首次提出。其属于一种经典的启发式搜索方法,所谓启发式搜索,就在于当前搜索结点往下选择下一步结点时,可以通过一个启发函数来进行选择,选择代价最少的结点作为下一步搜索结点而跳转其上。
传统的算法中,深度优先搜索(DFS)和广度优先搜索(BFS)在展开子结点时均属于盲目型搜索,也就是说,它不会选择哪个结点在下一次搜索中更优而去跳转到该结点进行下一步的搜索。在运气不好的情形中,均需要试探完整个解集空间, 显然,只能适用于问题规模不大的搜索问题中。而与DFS,BFS不同的是,一个经过仔细设计的启发函数,往往在很快的时间内就可得到一个搜索问题的最优解。
在原论文中,A*算法的步骤设计如下:
1、标记起点s为open,计算起点的估计代价 2、选择open点集中估计代价最小的点 3、如果选中的点∈目标集合T,即到达目标,标记该点closed,算法结束 4、否则,还未到达目标,标记该点closed,对其周围直达的点计算估计代价,如果周围直达的点未标记为closed,将其标记为open;如果已经标记为closed的,如果重新计算出的估计代价比它原来的估计代价小,更新估计代价,并将其重新标记open。返回第2步。

举个栗子:
例1:
如下图所示,初始时起点位置为5,需要前往位置20,每条路径上的数值代表从该路径经过的代价值。
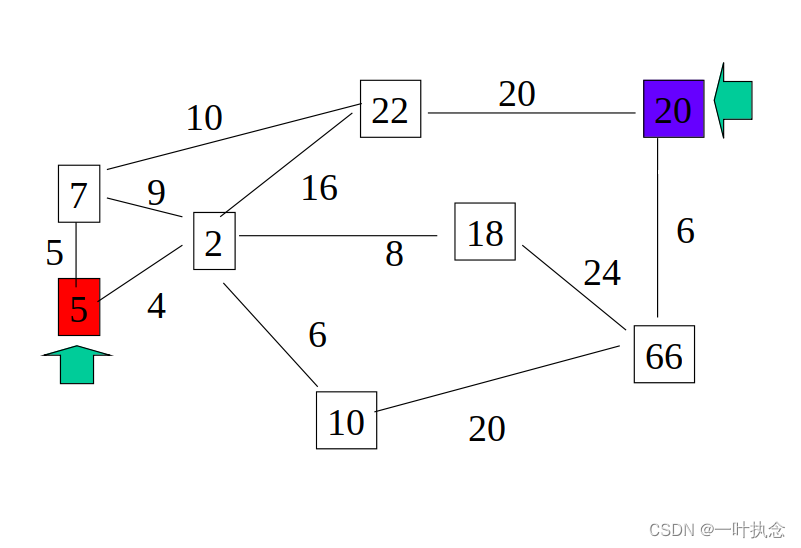
根据上述公式,首先设置5号点为起点,则它向下有两条路径:前往2号点与前往7号点。两条路径的代价值分别为4跟5。则根据代价函数,我们选择走代价值小一点的点,即前往2号点:
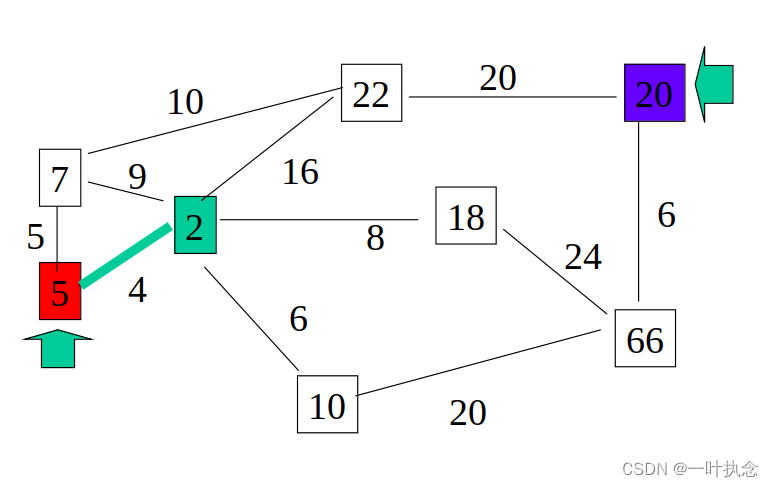
然后根据第三步判断是否到达终点,可知2不是终点。跳转第四步,标记该点位置,同时计算它到周围点的代价值:从2号点可以去7号点,代价值为9;可以去22号点,代价值为16;可以去18号点,代价值为18;可以去10号点,代价值为6。然后调转回第二步。
根据第二步,选择上述点中代价值最小的点,也就是10号点:
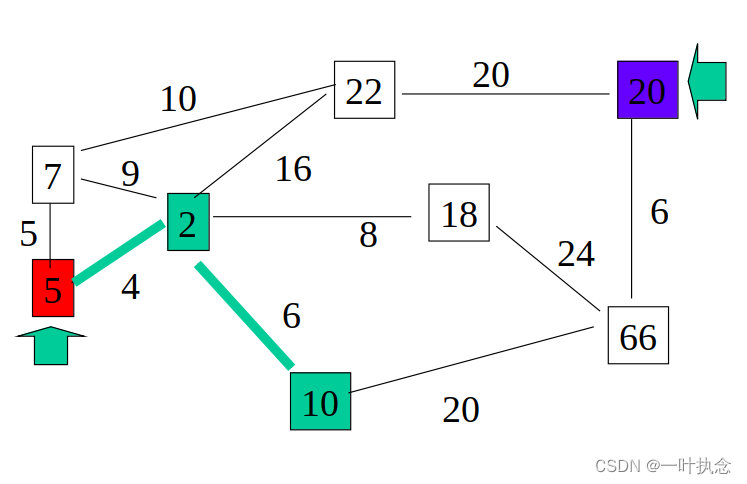
然后根据第三步判断是否到达终点,可知10不是终点。跳转第四步,标记该点位置,同时计算它到周围点的代价值:从10号点可以去66号点,代价值为20。
根据第二步,选择上述点中代价值最小的点,也就是66号点:
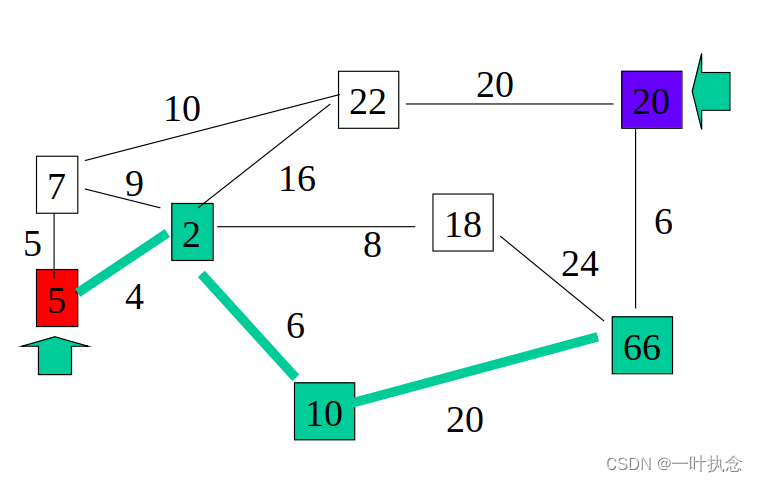
然后根据第三步判断是否到达终点,可知66不是终点。跳转第四步,标记该点位置,同时计算它到周围点的代价值:从66号点可以去20号点,代价值为6。
根据第二步,选择上述点中代价值最小的点,也就是20号点:
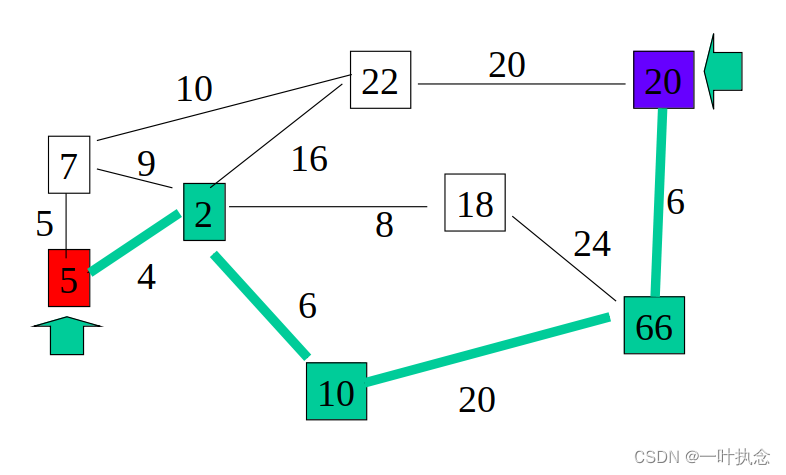
然后根据第三步判断是否到达终点,可知20号是终点,至此,算法结束。得到最优路径5->2->10->66->20。可以看到,A在搜索速度以及准确性上都是很高的,明显优于DFS与BFS。但是注意到一个问题。与Dijkstra不同的是,Dijkstra虽然基于BFS导致搜索速度比较低,但是它的搜索结果一定是最优的。而A虽然能够快速找到一条路径,但是它不一定是最优的。例如例2所示:
例2:
将例1中2到10的代价值从6改为10:
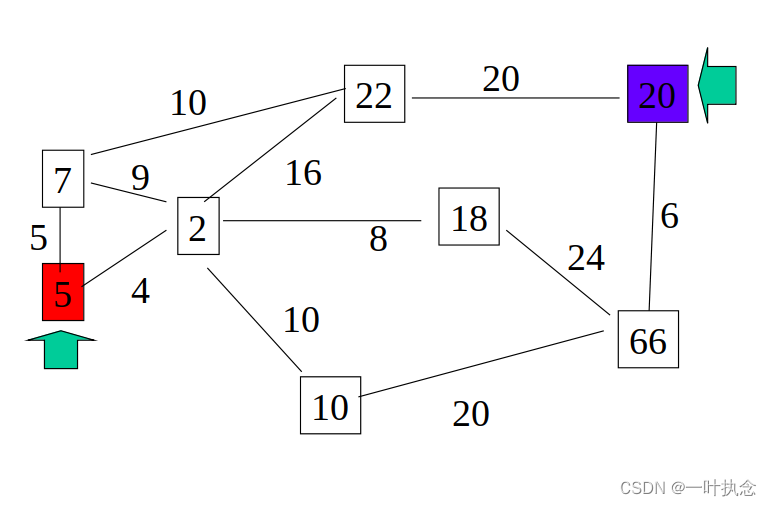
此时,按照上述方式得到的路径应该是:
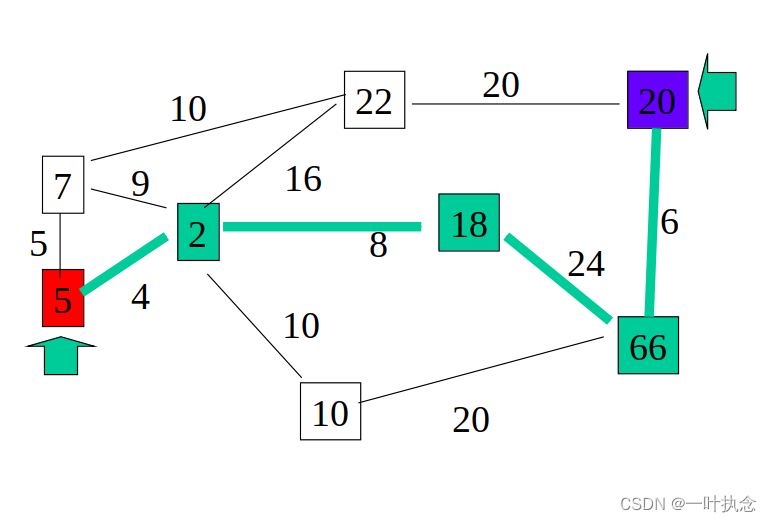
即通过5->2->18->66->20,总代价值为42。但是实际上从5->20的最优路径应该是5->2->10->66->20,总代价值为40。所以从这里我们也可以看出来,A*虽然在搜索速度上比Dijkstra要快很多,但是它的结果可能不是最优的。
A*与启发函数
看完了例子,对于A* 算法也有了一个初步的了解。那么对于A* 算法而言,它相对于其他算法的优点是什么呢?深度优先搜索的好处是时间快,但是很少能求出最优解;而广度优先搜索确实可以求出最优解,但由于广度优先搜索是一层层搜下去的,必须扩展每一个点,所以时间效率和空间效率都不高。而A* 算法恰可以解决这两个缺点:既有极大概率求出最优解,又可以减少冗余的时间。
那么对于A* 而言它的使用又有哪些需要注意的地方呢?最关键的一点就是在于它的启发函数的确定了,也就是确定上面例子中从一个点到另一个点的代价值。在原算法中,定义了一个代价函数:
f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n)
其中f[n]是 是从初始状态经由状态n到目标状态的代价估计,g(n)是从初始到n的实际代价,而h(n)是从n到目标状态的估计代价。
在g和h的估计中,h的估计方法是比较宽泛的,可以是直线距离,也可以是其他(如坐标和之类的),但作者提到,估计h必须要小于真实h才能保证算法是可接收到的,即能找到最优解。如果估计h比真实h大,则可能找到的的不是最优解。
那么设置h为0?可以,但就会变成类似Dijkstra算法,会找到到达地图上各点的最优路线。最终一定也会到达目标集合T中的节点,并标记closed结束算法,但过程中会展开更多无谓的节点,漫无目的地展开。所以,A*算法中很重要的一点就在于这个h的选择。
A*算法与路径规划
A*在移动机器人的路径规划中使用的也非常广泛,对于需要求出一条起点到终点的有效路径的情况下是一种非常合适的算法。
举个非常经典的例子:
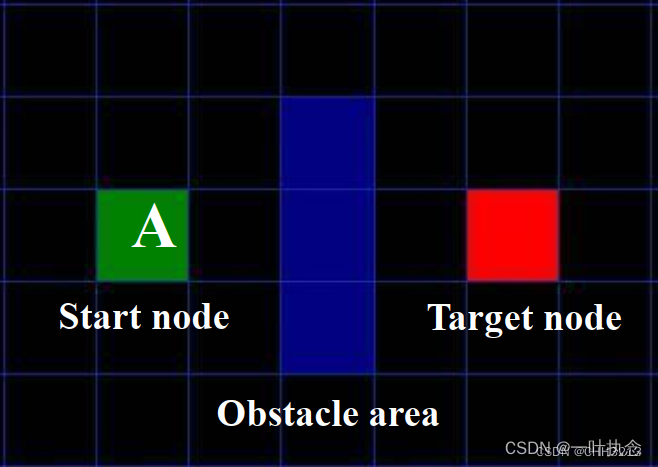
从图中的绿色方块运动到红色方块,蓝色为障碍物。首先,我们把地图栅格化,把每一个方格的中心称为节点;这个特殊的方法把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子,它的状态就是可走 (walkalbe) 和不可走 (unwalkable) 。通过计算出从 A 到 目标点需要走过哪些方格,就找到了路径。一旦路径找到了,便从一个方格的中心移动到另一个方格的中心,直至到达目的地。

一旦我们把搜寻区域简化为一组可以量化的节点后,我们下一步要做的便是查找最短路径。在 A* 中,我们从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标:
1、从起点 A 开始,定义A为父节点,并把它加入到 openList中。现在 openList 里只有起点 A ,后面会慢慢加入更多的项。
2、如上图所示,父节点A周围共有8个节点,定义为子节点。将子节点中可达的(reachable)或者可走的(walkable)放入openList中,成为待考察对象。
3、若某个节点既未在openList,也没在closeList中,则表明还未搜索到该节点。
4、初始时, 节点A离自身距离为0,路径完全确定,将其移入closeList中; closeList 中的每个方格都是现在不需要再关注的。
5、路径优劣判断依据是移动代价,单步移动代价采取Manhattan 计算方式(即 d = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d=|x_1-x_2|+|y_1-y_2| d=∣x1−x2∣+∣y1−y2∣),即把横向和纵向移动一个节点的代价定义为10。斜向移动代价为14
6、现在openList = {B,C,D,E,F,G,H,I}, closeList = {A}
下面我们需要去选择节点A相邻的子节点中移动代价 f 最小的节点,下面以节点I的计算为例。
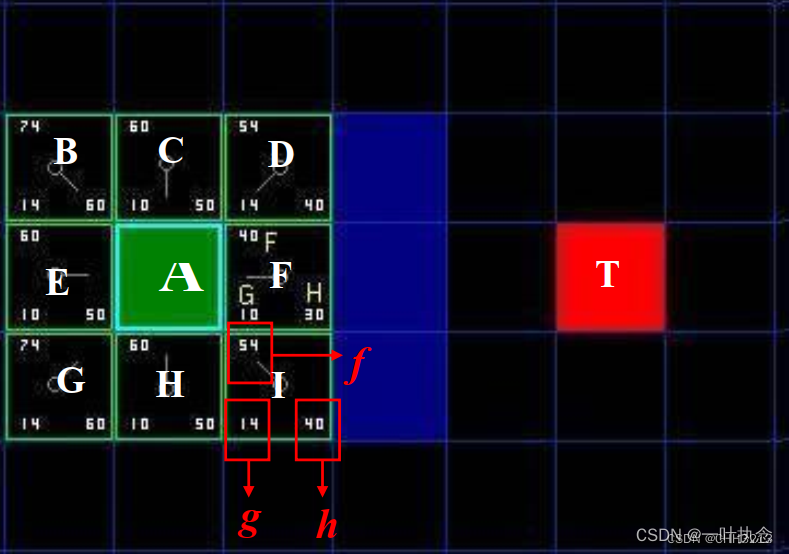
移动代价评价函数为: f ( n ) = g ( n ) + h ( n )。 f ( n )是从初始状态经由状态n到目标状态的代价估计, g ( n ) 是在状态空间中从初始状态到状态n的实际代价, h ( n ) 是从状态n到目标状态的最佳路径的估计代价。
首先考察 g,由于从A到该格子是斜向移动,单步移动距离为14,故 g = 14.
再考察估计代价 h。估计的含义是指忽略剩下的路径是否包含有障碍物(不可走), 完全按照Manhattan计算方式,计算只做横向或纵向移动的累积代价:横向向右移动3步,纵向向上移动1步,总共4步,故为 h = 40.
因此从A节点移动至I节点的总移动代价为: f = g + h = 54
以此类推,分别计算当前openList中余下的7个子节点的移动代价 f ,从中挑选最小代价节点F,移到closeList中。
现在openList = {B,C,D,E,G,H,I}, closeList = {A,F}
然后继续往下搜索:
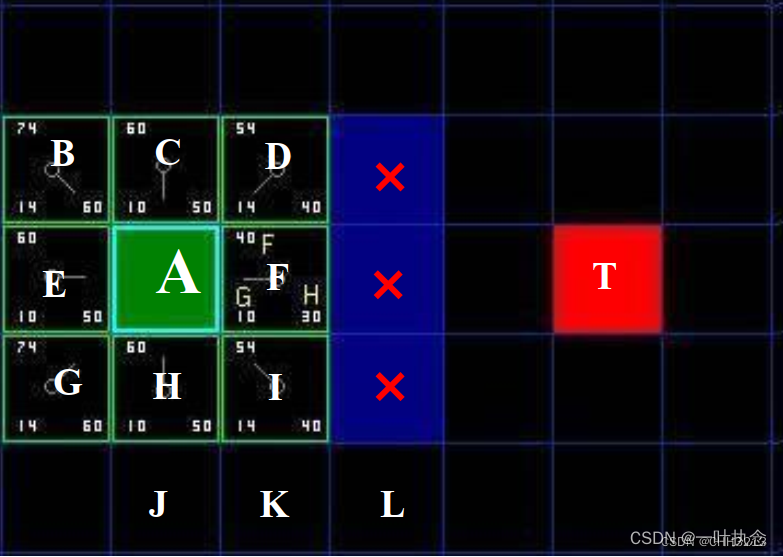
从openList中选择 f 值最小的 ( 方格 ) 节点I(D节点的 f值跟I相同,任选其一即可,不过从速度上考虑,选择最后加入 openList 的方格更快。这导致了在寻路过程中,当靠近目标时,优先使用新找到的方格的偏好。 对相同数据的不同对待,只会导致两种版本的 A* 找到等长的不同路径 ),从 openList里取出,放到 closeList 中。
检查所有与它相邻的子节点,忽略不可走 (unwalkable) 的节点、以及忽略已经存在于closeList的节点;如果方格不在openList中,则把它们加入到 openList中,并把它们作为节点I的子节点 。
如果某个相邻的节点(假设为X)已经在 opeLlist 中,则检查这条路径是否更优,也就是说经由当前节点( 我们选中的节点)到达节点X是否具有更小的 g 值。如果没有,不做任何操作。否则,如果 g 值更小,则把X的父节点设为当前方格 ,然后重新计算X的 f 值和 g 值。
判断完所有子节点后,现在openList = {B,C,D,E,G,H,J,K,L}, closeList = {A,F,I}
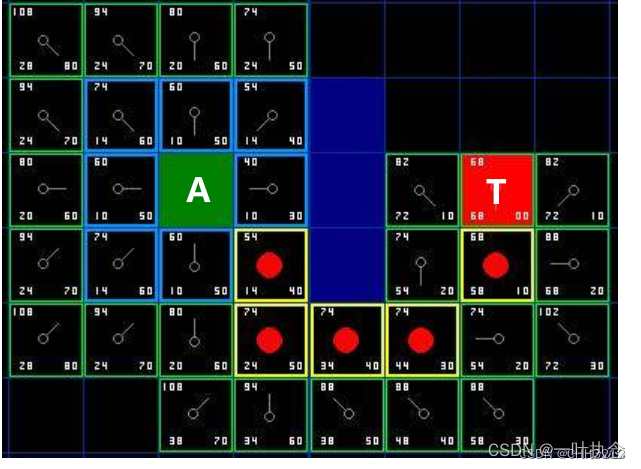
依次类推,不断重复。一旦搜索到目标节点T,完成路径搜索,结束算法。
完成路径搜索后,从终点开始,向父节点移动,这样就被带回到了起点,这就是搜索后的路径。如下图所示。从起点 A 移动到终点 T就是简单从路径上的一个方格的中心移动到另一个方格的中心,直至目标。
代码实现
import os
import sys
import math
import heapq
import matplotlib.pyplot as plt
class AStar:
"""AStar set the cost + heuristics as the priority
"""
def __init__(self, s_start, s_goal, heuristic_type,xI, xG):
self.s_start = s_start
self.s_goal = s_goal
self.heuristic_type = heuristic_type
self.u_set = [(-1, 0), (0, 1),
(1, 0), (0, -1)] # feasible input set
self.obs = self.obs_map() # position of obstacles
self.OPEN = [] # priority queue / OPEN set
self.CLOSED = [] # CLOSED set / VISITED order
self.PARENT = dict() # recorded parent
self.g = dict() # cost to come
self.x_range = 51 # size of background
self.y_range = 31
self.xI, self.xG = xI, xG
self.obs = self.obs_map()
def update_obs(self, obs):
self.obs = obs
def animation(self, path, visited, name):
self.plot_grid(name)
self.plot_visited(visited)
self.plot_path(path)
plt.show()
def plot_grid(self, name):
obs_x = [x[0] for x in self.obs]
obs_y = [x[1] for x in self.obs]
plt.plot(self.xI[0], self.xI[1], "bs")
plt.plot(self.xG[0], self.xG[1], "gs")
plt.plot(obs_x, obs_y, "sk")
plt.title(name)
plt.axis("equal")
def plot_visited(self, visited, cl='gray'):
if self.xI in visited:
visited.remove(self.xI)
if self.xG in visited:
visited.remove(self.xG)
count = 0
for x in visited:
count += 1
plt.plot(x[0], x[1], color=cl, marker='o')
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if count < len(visited) / 3:
length = 20
elif count < len(visited) * 2 / 3:
length = 30
else:
length = 40
#
# length = 15
if count % length == 0:
plt.pause(0.001)
plt.pause(0.01)
def plot_path(self, path, cl='r', flag=False):
path_x = [path[i][0] for i in range(len(path))]
path_y = [path[i][1] for i in range(len(path))]
if not flag:
plt.plot(path_x, path_y, line, color='r')
else:
plt.plot(path_x, path_y, line, color=cl)
plt.plot(self.xI[0], self.xI[1], "bs")
plt.plot(self.xG[0], self.xG[1], "gs")
plt.pause(0.01)
def update_obs(self, obs):
self.obs = obs
def obs_map(self):
"""
Initialize obstacles' positions
:return: map of obstacles
"""
x = 51
y = 31
obs = set()
for i in range(x):
obs.add((i, 0))
for i in range(x):
obs.add((i, y - 1))
for i in range(y):
obs.add((0, i))
for i in range(y):
obs.add((x - 1, i))
for i in range(10, 21):
obs.add((i, 15))
for i in range(15):
obs.add((20, i))
for i in range(15, 30):
obs.add((30, i))
for i in range(16):
obs.add((40, i))
return obs
def searching(self):
"""
A_star Searching.
:return: path, visited order
"""
self.PARENT[self.s_start] = self.s_start
self.g[self.s_start] = 0
self.g[self.s_goal] = math.inf
heapq.heappush(self.OPEN,
(self.f_value(self.s_start), self.s_start))
while self.OPEN:
_, s = heapq.heappop(self.OPEN)
self.CLOSED.append(s)
if s == self.s_goal: # stop condition
break
for s_n in self.get_neighbor(s):
new_cost = self.g[s] + self.cost(s, s_n)
if s_n not in self.g:
self.g[s_n] = math.inf
if new_cost < self.g[s_n]: # conditions for updating Cost
self.g[s_n] = new_cost
self.PARENT[s_n] = s
heapq.heappush(self.OPEN, (self.f_value(s_n), s_n))
return self.extract_path(self.PARENT), self.CLOSED
def get_neighbor(self, s):
"""
find neighbors of state s that not in obstacles.
:param s: state
:return: neighbors
"""
return [(s[0] + u[0], s[1] + u[1]) for u in self.u_set]
def cost(self, s_start, s_goal):
"""
Calculate Cost for this motion
:param s_start: starting node
:param s_goal: end node
:return: Cost for this motion
:note: Cost function could be more complicate!
"""
if self.is_collision(s_start, s_goal):
return math.inf
return math.hypot(s_goal[0] - s_start[0], s_goal[1] - s_start[1])
def is_collision(self, s_start, s_end):
"""
check if the line segment (s_start, s_end) is collision.
:param s_start: start node
:param s_end: end node
:return: True: is collision / False: not collision
"""
if s_start in self.obs or s_end in self.obs:
return True
if s_start[0] != s_end[0] and s_start[1] != s_end[1]:
if s_end[0] - s_start[0] == s_start[1] - s_end[1]:
s1 = (min(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
s2 = (max(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
else:
s1 = (min(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
s2 = (max(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
if s1 in self.obs or s2 in self.obs:
return True
return False
def f_value(self, s):
"""
f = g + h. (g: Cost to come, h: heuristic value)
:param s: current state
:return: f
"""
return self.g[s] + self.heuristic(s)
def extract_path(self, PARENT):
"""
Extract the path based on the PARENT set.
:return: The planning path
"""
path = [self.s_goal]
s = self.s_goal
while True:
s = PARENT[s]
path.append(s)
if s == self.s_start:
break
return list(path)
def heuristic(self, s):
"""
Calculate heuristic.
:param s: current node (state)
:return: heuristic function value
"""
heuristic_type = self.heuristic_type # heuristic type
goal = self.s_goal # goal node
if heuristic_type == "manhattan":
return abs(goal[0] - s[0]) + abs(goal[1] - s[1])
else:
return math.hypot(goal[0] - s[0], goal[1] - s[1])
def main():
s_start = (5, 5)
s_goal = (45, 25)
astar = AStar(s_start, s_goal, "euclidean",s_start,s_goal)
path, visited = astar.searching()
astar.animation(path, visited, "A*") # animation
if __name__ == '__main__':
main()
效果如下:
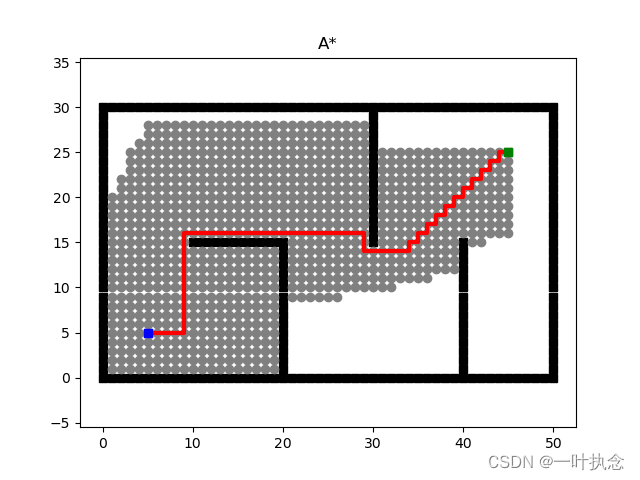
简单解析一下:
在获取起点后,算法维护了两个字典:
self.PARENT[self.s_start] = self.s_start
self.g[self.s_start] = 0
self.g[self.s_goal] = math.inf
PARENT字典中存取的是这个点由哪个点延伸出来的,即它的上一个节点是谁,用于最后的路径的返回;g这个字典中存储的是每个坐标的代价值,即g[s]。
然后,算法通过堆栈的概念维护了一个堆栈:
heapq.heappush(self.OPEN,(self.f_value(self.s_start), self.s_start))
将初始值的f[s]存储在这里,然后进行while循环:
首先从堆栈中取出栈顶元素:
_, s = heapq.heappop(self.OPEN)
注意到这里使用的heapq堆栈功能中的两个函数heapq.heappop与heapq.heappush。heappop会取出栈顶元素并将原始数据从堆栈中删除,而heappush则是对插入的数据按大小排序并存储在堆栈中。所以每一个遍历的点都会按照它的代价值放入堆栈中,同时每次取出的都是代价值最小的那个。
然后判断出栈顶元素是否为目标点,如果为目标点,则退出:
if s == self.s_goal: # stop condition
break
如果不是,则更新该点附近点的代价值:
for s_n in self.get_neighbor(s):
for s_n in self.get_neighbor(s):
new_cost = self.g[s] + self.cost(s, s_n)
if s_n not in self.g:
self.g[s_n] = math.inf
if new_cost < self.g[s_n]: # conditions for updating Cost
self.g[s_n] = new_cost
self.PARENT[s_n] = s
heapq.heappush(self.OPEN, (self.f_value(s_n), s_n))
get_neighbor为获取该点周围的点的坐标。heappush入栈时需要存储的该点的代价值的计算方式为:
def f_value(self, s):
"""
f = g + h. (g: Cost to come, h: heuristic value)
:param s: current state
:return: f
"""
return self.g[s] + self.heuristic(s)
其中self.g[s]为A算法中的g,self.heuristic(s)为A算法中的h。而作为一个启发函数,h的计算可以根据实际情况进行选择,例如在栅格地图中,计算h的方式一般可以分为两种:曼哈顿距离与欧几里德距离。
欧式距离是我们平时用的比较多的,即求两点之间的直线长度:
else:#sqrt(x^2+y^2)
return math.hypot(goal[0] - s[0], goal[1] - s[1])
而曼哈顿距离相对不是那么普遍,简单的来说,就是找到一个当前点到终点的X方向需要走过的格子的数量以及Y方向需要走过的格子数量。:
if heuristic_type == "manhattan":
return abs(goal[0] - s[0]) + abs(goal[1] - s[1])
应用这两种不同的计算方式,会得到不同的效果:
采用曼哈顿距离计算的结果:
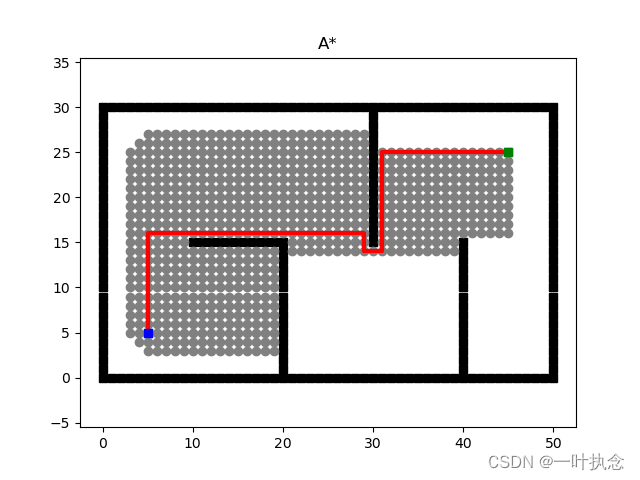
采用欧式距离计算的结果:
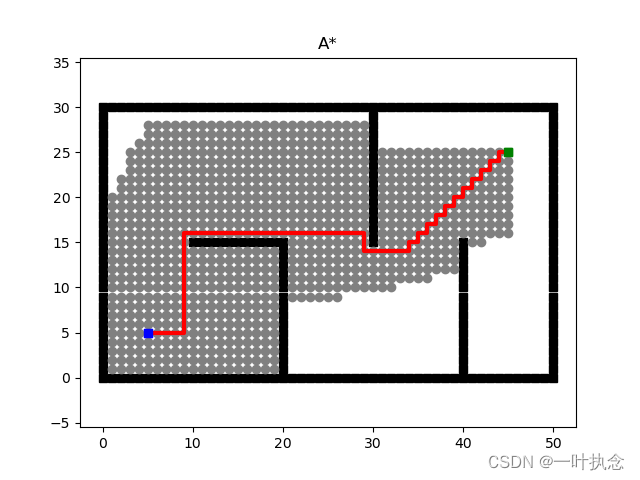
可以看到采用不同的h的方式遍历的结果会有一定的差异。除此之外,在对周围点进行搜索的时候的点的选择也会对算法的遍历产生影响,例如上面的代码中u_set设置为:
self.u_set = [(-1, 0), (0, 1),
(1, 0), (0, -1)] # feasible input set
即每个点只能搜索前后左右四个点。但是如果将其改为搜索8个点的话,得到的搜索结果就会变成:
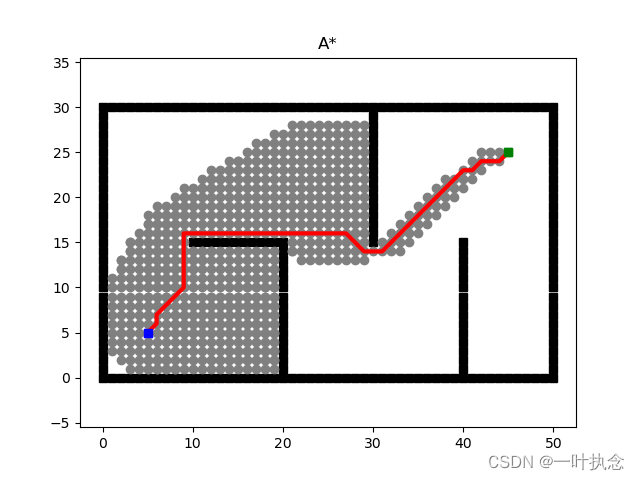
至此,A*算法的简单原理整理完毕。
参考:
1、 十五个经典算法研究与总结(1)-A*搜索算法
2、【全局路径规划】A算法 A Search Algorithm
3、【路径规划】全局路径规划算法——A*算法(含python实现 | c++实现)
4、 路径规划之 A* 算法














