目录

一、前言

（1）分治算法

（2）分治算法解题方法

    1.分解：

    2.治理：

    3.合并：

二、快速排序

1.问题分析

2.算法设计

    （1）分解：

    （2）治理 ：

    （3）合并：

    （4）基准元素的选取：

3.算法分析

三、AC代码

 四、共勉

---

一、前言

（1）分治算法

    快速排序，其实是一种分治算法，那么在了解快速排序之前，我们先来看看什么是分治算法。在算法设计中，我们引入分而治之的策略，称为分治算法，其本质就是将一个大规模的问题分解为若干个规模较小的相同子问题，分而治之。

（2）分治算法解题方法

    1.分解：

    将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。

    2.治理：

    求解各个子问题。由于各个子问题与原问题形式相同，只是规模较小而已，而当子问题划分得足够小时，就可以用简单的方法解决。

    3.合并：

    按原问题的要求，将子问题的解逐层合并构成原问题的解。

二、快速排序

1.问题分析

    快速排序是比较快的排序方法。它的基本思想是通过一组排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据小，然后再按此方法对这两部分数据进行快速排序，整个排序过程可以递归进行，以此使所有数据变成有序序列。

2.算法设计

    （1）分解：

    先从数列中取出一个元素作为基准元素。一基准元素为标准，将问题分解为两个子序列，使小于或者等于基准元素的子序列在左侧，使大于基准元素的子序列在右侧。

    （2）治理 ：

    对两个子序列进行快速排序（递归快速排序）。

    （3）合并：

    将排好的两个子序列合并在一起，得到原问题的解。

    （4）基准元素的选取：

    ①：取第一个元素。(通常选取第一个元素)

    ②：取最后一个元素

    ③：取中间位置的元素

    ④：取第一个、最后一个、中间位置元素三者之中位数

    ⑤：取第一个和最后一个之间位置的随机数 k (low<=k<=hight)

3.算法分析

    假设当前的待排序的序列为 R[low,hight] ， 其中 low<=hight。同时选取首元素为基准元素。

步骤一：选取首元素的第一个元素作为基准元素  pivot=R[low] ，i=low ，j=hight。

步骤二：从右向左扫描，找到小于等于 pivot 的数，如果找到，R[i] 和 R[j] 交换 ，i++。

步骤三：从左向右扫描，找到大于 pivot 的数，如果找到，R[i] 和 R[j] 交换，j--。

步骤四：重复 步骤二~步骤三，直到  j 与 i 的指针重合 返回位置 mid=i ，该位置的数正好是 pivot 元素。

    至此换成一趟排序，此时以 mid 为界线，将数据分割为两个子序列，左侧子序列都比 pivot 数小，右侧子序列都比 pivot 数大，然后再分别对这两个子序列进行快速排序。  

    下面我将以序列（30，24，5，58，18，36，12，42，39）为例，进行图解。

（1）初始化。i=low ，j=hight，pivot=R[low]=30。如下图所示：

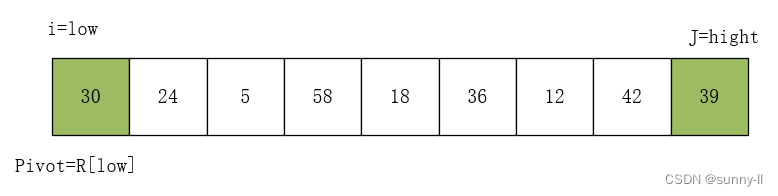
 （2）向左走，从数组的右边位置向左找，一直找到小于等于 pivot 的数，找到R[j]=12，R[i]与R[j]交换，i++。如下图所示：

 

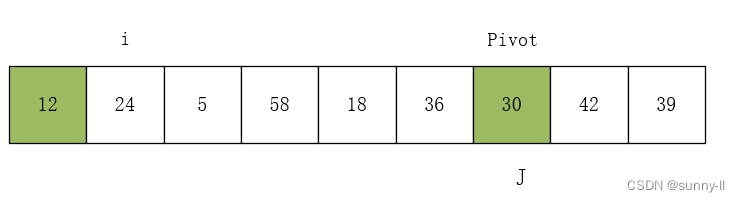
（3）向右走，从数组的左边位置向右找，一直找到比 pivot 大的数，找到 R[i]=58 ,R[i] 与 R[j] 交换 ，j--。

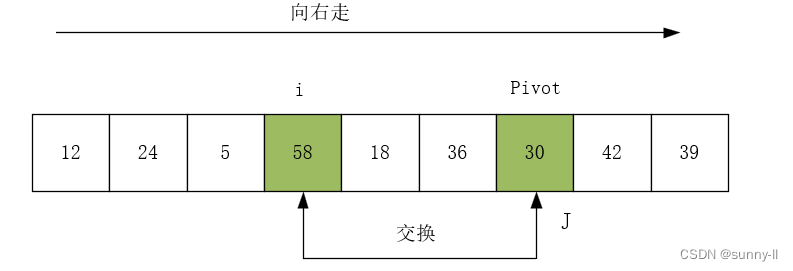
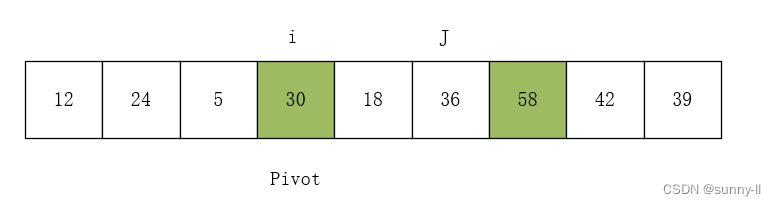 （4）向左走，从数组的右边位置向左找，一直找到小于等于 pivot 的数，找到R[j]=18，R[i]与R[j]交换，i++。如下图所示：

 

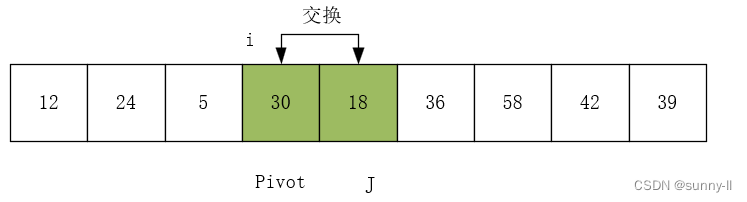
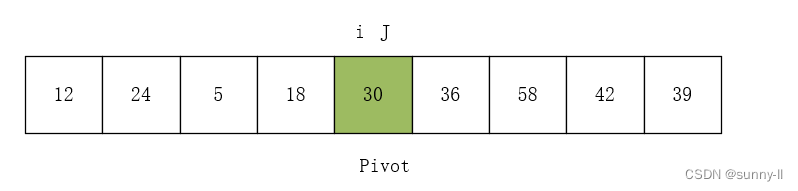 （5）向右走，从数组的左边位置向右找，一直找到比 pivot 大的数，这是 i=j，第一轮排序结束，返回 i 的位置，mid=i 。以上的操作是对序列进行分解，其代码如下图所示：

int part(int* r, int low, int hight)  //划分函数
{
	int i = low, j = hight, pivot = r[low]; //基准元素
	while (i < j)
	{
		while (ipivot) //从右向左开始找一个 小于等于 pivot的数值
		{
			j--;
		}
		if (i < j)
		{
			swap(r[i++], r[j]);  //r[i]和r[j]交换后 i 向右移动一位
		}
		while (i < j && r[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
		{
			i++;
		}
		if (i < j)
		{
			swap(r[i], r[j--]);  //r[i]和r[j]交换后 i 向左移动一位
		}
	}
	return i;  //返回最终划分完成后基准元素所在的位置
}

（6）然后在分别对这两个序列（12，24，5，18）和（36，58，42，39）进行快速排序（递归）。其代码如下图所示：

void Quicksort(int* r, int low, int hight)
{
	int mid;
	if (low < hight)
	{
		mid = part(r, low, hight);  // 返回基准元素位置
		Quicksort(r, low, mid - 1); // 左区间递归快速排序
		Quicksort(r, mid+1, hight); // 右区间递归快速排序
	}
}

三、AC代码

#include 
#include 
#include 
#include 
using namespace std;
int part(int* r, int low, int hight)  //划分函数
{
	int i = low, j = hight, pivot = r[low]; //基准元素
	while (i < j)
	{
		while (ipivot) //从右向左开始找一个 小于等于 pivot的数值
		{
			j--;
		}
		if (i < j)
		{
			swap(r[i++], r[j]);  //r[i]和r[j]交换后 i 向右移动一位
		}
		while (i < j && r[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
		{
			i++;
		}
		if (i < j)
		{
			swap(r[i], r[j--]);  //r[i]和r[j]交换后 i 向左移动一位
		}
	}
	return i;  //返回最终划分完成后基准元素所在的位置
}
void Quicksort(int* r, int low, int hight)
{
	int mid;
	if (low < hight)
	{
		mid = part(r, low, hight);  // 返回基准元素位置
		Quicksort(r, low, mid - 1); // 左区间递归快速排序
		Quicksort(r, mid+1, hight); // 右区间递归快速排序
	}
}
int main()
{
	int a[10001];
	int  N;
	cout << "请输入要排序的数据的个数： " << endl;
	cin >> N;
	cout << "请输入要排序的数据： " << endl;
	for (int i = 0; i < N; i++)
	{
		cin >> a[i];
	}
	cout << endl;
	Quicksort(a, 0, N - 1);
	cout << "排序后的序列为： " << endl;
	for (int i = 0; i < N; i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
	return 0;
}

 四、共勉

    以下就是我对分治：快速排序的理解，如果有不懂和发现问题的小伙伴，请在评论区说出来哦，同时我还会继续更新对分治算法的理解，请持续关注我哦！！！！！！！！