- 监听Redis中Key值的变化(SpringBoot整合)
- Python副业技术总结,手把手教你用宝塔面板部署Django程序
- 深入浅出 Spring Boot 3.x:从原理到实战,全面解锁 Ja
- MySQL用户与权限管理
- ruoyi-vue(若依前后端分离版本)环境搭建 用idea 安装re
- 新零售门店、商品、会员管理指标体系总览
- 抖音六神最新算法
- Java项目:基于Springboot框架实现的校园求职招聘系统(sp
- 使用Navicat导出导出 MySQL 数据库表结构、表数据到Exce
- 第十三届蓝桥杯Java B 组国赛 C 题——左移右移(AC)
- Spring Boot集成百度UidGenerator雪花算法使用以及
- OpenAI 推出新网络爬虫GPTBot,为GPT-5做准备
- 【Consul】基于Golang实现Consul服务的注册、注销、修改
- 简单易懂:Axios 如何取消请求的两种方法
- 无人新零售引领的创新浪潮
- 一个开源跨平台嵌入式USB设备协议:TinyUSB
- 【爬虫实战】使用Python获取花粉俱乐部中Mate60系列的用户发帖
- mysql如何自定义自增主键值,以及所遇到的不生效问题
- 详解:-bash: mysql command not found (
- MySQL高可用解决方案――从主从复制到InnoDB Cluster架
- 【Linux】使用Jenkins + svn + springboot
- nuxt服务端渲染注意事项及nuxt内存溢出解决
- 爬个数据这么吃力?别慌,代理IP轻松解决跨境电商技术瓶颈
- 推荐系统算法 协同过滤算法详解(三)Springboot 实现基于用户
- 深入OceanBase内部机制:多租户架构下的资源隔离实现精讲
- Java校园失物招领系统设计与实现(Idea+Springboot+m
- 基于Springboot的毕业论文管理系统的设计与实现
- Spring AOP的实现方式与原理
- 【Rust】——提取函数消除重复代码和泛型
- 大语言模型LLM《提示词工程指南》学习笔记05

🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
喜欢大数据分析项目的小伙伴,希望可以多多支持该系列的其他文章
| 大数据分析案例-基于随机森林算法预测人类预期寿命 |
| 大数据分析案例-基于随机森林算法的商品评价情感分析 |
| 大数据分析案例-用RFM模型对客户价值分析(聚类) |
| 大数据分析案例-对电信客户流失分析预警预测 |
| 大数据分析案例-基于随机森林模型对北京房价进行预测 |
| 大数据分析案例-基于RFM模型对电商客户价值分析 |
| 大数据分析案例-基于逻辑回归算法构建垃圾邮件分类器模型 |
| 大数据分析案例-基于决策树算法构建员工离职预测模型 |
| 大数据分析案例-基于KNN算法对茅台股票进行预测 |
| 大数据分析案例-基于多元线性回归算法构建广告投放收益模型 |
| 大数据分析案例-基于随机森林算法构建返乡人群预测模型 |
| 大数据分析案例-基于决策树算法构建金融反欺诈分类模型 |
目录
1.实验背景
1.1背景概述
1.2实验目的
2.数据来源及方法介绍
2.1 数据来源
2.2 属性介绍
2.3 算法介绍
2.3.1 决策树
2.3.2 朴素贝叶斯法
2.3.3 KNN
3、实验步骤
3.1导入模块和数据
3.2特征工程
3.2.1特征工程介绍
3.2.2数据预处理
3.2.3特征选择
3.3数据可视化
3.3.1对职务分布可视化
3.3.2对年龄分布可视化
3.4模型构建
3.4.1拆分训练集测试集
3.4.2导入并拟合模型
3.5模型评估
3.5.1 Recall和Precision评估
3.5.2 ROC曲线评估
4 实验总结
源代码
1.实验背景
1.1背景概述
银行客户流失是指银行的客户终止在该行的所有业务并销号。但在实际运营中,对于具体业务部门,银行客户流失可以定位为特定的业务终止行为。商业银行的客户流失较为严重,流失率可达20%。而获得新客的成本是维护老客户的5倍。因此,从海量客户交易数据中挖掘出对流失有影响的信息,建立高效的客户流失预警体系尤为重要。
客户流失的主要原因有:价格流失、产品流失、服务流失、市场流失、促销流失、技术流失、政治流失。有些时候表面上是价格导致的客户流失,但实际上多重因素共同作用导致了客户的流失。比如说,不现实的利润目标、价格结构的不合理、业务流程过于复杂、组织结构的不合理等等。维护客户关系的基本方法:追踪制度,产品跟进,扩大销售,维护访问,机制维护。
因此建立量化模型,合理预测客群的流失风险是很有必要的。比如:常用的风险因子,客户持有的产品数量、种类,客户的年龄、性别,地理区域的影响,产品类别的影响,交易的时间间隔,促销的手段等等。根据这些因素及客户流失的历史数据对现有客户进行流失预测,针对不同的客群提供不同的维护手段,从而降低客户的流失率。
1.2实验目的
时代与技术的发展使得数据的获取与挖掘成为可能,本实验将通过python对用户做特征分析和顾客流失分析,帮助银行发现并改善顾客体验,以及确定挽留的目标顾客并帮助银行制定方案。
2.数据来源及方法介绍
2.1 数据来源
本次大数据课设实验中,我们小组所用到的银行客户信息数据来源于美林数据技术股份有限公司的公司产品人工智能平台(TEMPO)。数据集包括各个分行支行的银行客户数据。数据包含52类银行客户信息数据,我们将年龄、职务、存款、基金等51个变量作为自变量,将客户是否流失作为因变量。这些数据可用于生成智能计算工具,借此预测银行客户流失情况。
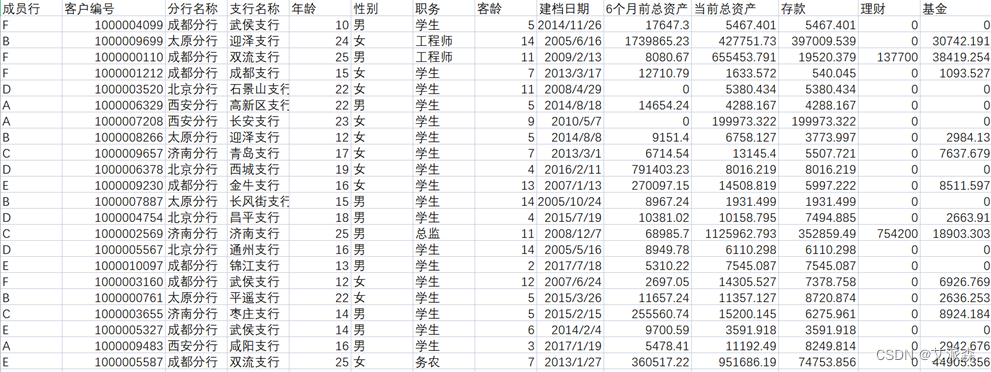
2.2 属性介绍
数据共包括52个属性,下面对各属性进行说明:
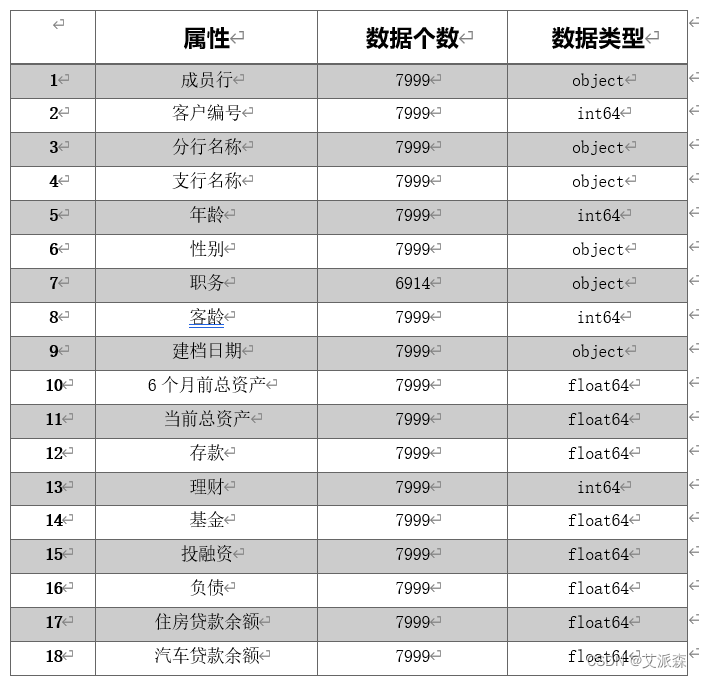
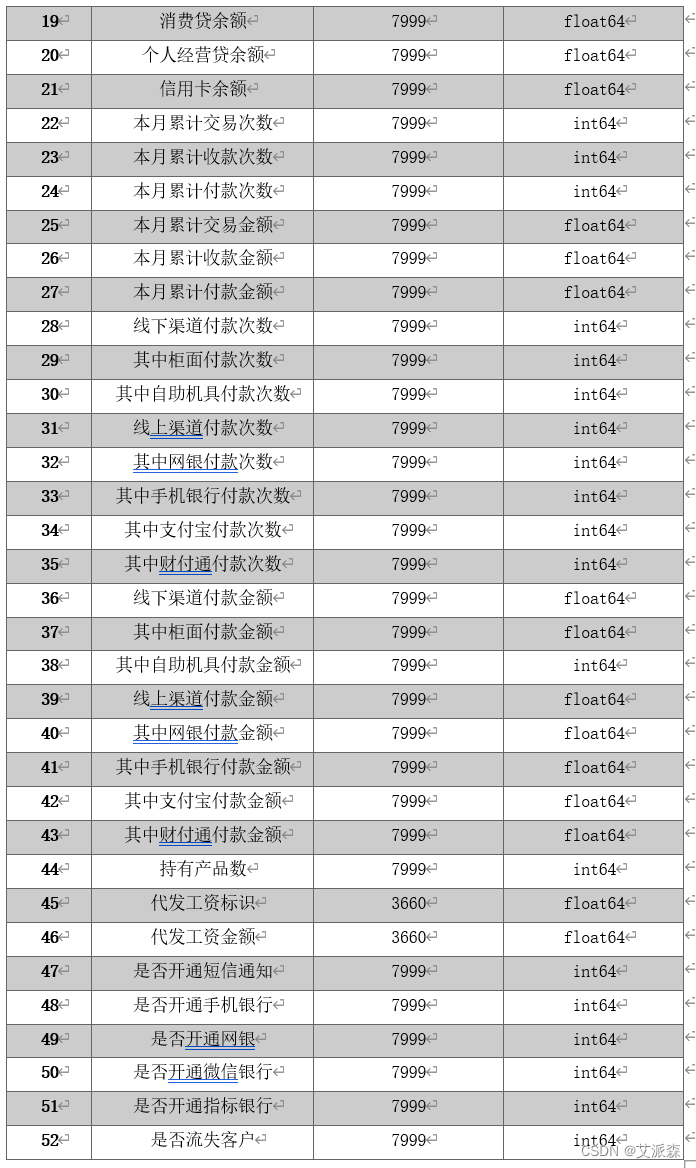
为了提高数据分类与分析的准确性,我们对原始数据进行了处理,对部分数据进行删除,以此减少无关数据的干扰,删去的数据如表所示:
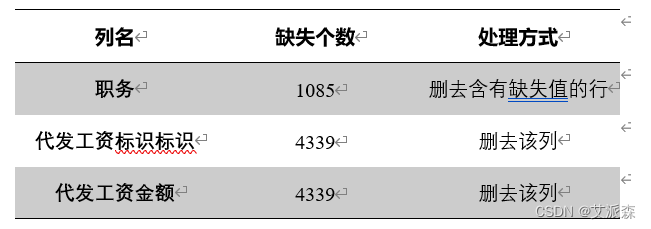
2.3 算法介绍
传统的机器学习分类方法就是根据现有的数据资料和分析成果进行建模,探索出规律并能对新的数据进行分类预测的技术,目前主要的算法非常多,有决策树(decision tree,DT)、神经网络、支持向量机(support vector machine,SVM)和随机森林(random forest,RF)等。而我们本次课设实验中,选择了以下三种算法,它们分别是决策树法、朴素贝叶斯法和k-近邻算法(KNN)。
2.3.1 决策树
(1)决策树简介
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构建决策树来进行分析的一种方式,是一种直观应用概率分析的一种图解法,即用一个类似于流程图的树形结构的算法,树内部的每一个节点代表的是对一个特征的测试,树的分支代表该特征的每一个测试结果,而树的每一个叶子节点代表一个类别。树的最高层是就是根节点。下图即为一个决策树的示意描述,内部节点用矩形表示,叶子节点用椭圆表示。
决策树算法具体是根据某种分割规则,将根节点按设定的阈值,分为两个子节点,并在子节点重复这个步骤,直到得出类别结果。若是将这个过程用流程图形式显示,就类似于一个二叉树,如图 2所示,N0是根节点,没有入边但有零或两条出边(edge),指向两个内节点(internal node),即Ni(2,3,4);内节点有一条入边、两条出边,出边指向终节点(terminal node),即最终的分类结果Cr。
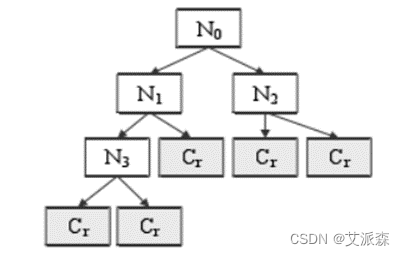
(2)决策树的构建原理
决策树的构建原理大致为给定一个样本集D={ω1,……,ωn } ,根据概率分布 P 从空间 Ω 抽取 N 个独立样本,寻找一个分类树Tr使得误分率函数Rp达到最小。决策树中,根节点和内节点都有一个属性条件Xt,Xt∈{X1,,。。。,Xm},用来分割不同分类结果的记录,因此称其为分割变量。所以,分类决策树最重要的问题就是如何选择最佳分割特征。
(3)决策树的基本算法
决策树中用来筛选特征的常用的算法有 1979 年提出的 ID3 算法、1984 年提出的 CART 算法和 1993 年提出的 C4.5算法,其中 CART 最为常见,下表为他们的大致区别:
| 算法 | 支持模型 | 树结构 | 特征选择 | 连续值处理 | 缺失值处理 | 剪枝 | ||
| ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 | ||
| C4.5 | 分类 | 多叉树 | 信息增益率 | 支持 | 支持 | 支持 | ||
| CART | 分类、回归 | 二叉树 | 基尼系数、均方差 | 支持 | 支持 | 支持 | ||
此处需要引入增益的概念,即父节点和子节点间不纯度的差。CART 遍历自变量的所有可能值,来得到使得不纯度增益∆t(t)最大时的点作为最佳分割点。决策树的分类实质上就是选择最大化增益,即最小化不纯性度量的加权平均值。现在设父节点、左子节点、右子节点分别为:tp、tl、tr ,分别来解释现在常用的三种度量方法:CART 中的 Gini 指数法、ID3 中的信息增益法和C4.5的增益比率法。
1. Gini指数法
Gini 指数是使用最广泛的一种分割方式,CART 使用的就是此方法,其不纯度i(t) 见式:
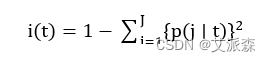
在上式中,J表示分类总数,p(j/t)表示在节点t中,属于j类的条件概率,对样本而言,表示第j类样本的占比。由此可以得到不纯度增益∆i(t) ,如(2.3)式所示:
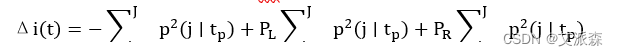
Gini 指数所指的最优分割就是要求式(2.4)达到最大时的分割。
2. 信息增益法(information gain)
该方法的思想就是用尽量少的东西得到更多结果。首先计算每个特征的信息增益,选择最高的一个来做分裂节点。利用熵值(entropy)来度量不纯度函数i(t),如式(2.5)所示。
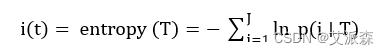
父子节点熵值的差即为信息增益,如式(2.6)所示:
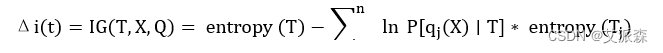
3. 增益比率法(gain ratio)
增益比率法是信息增益的改进,可以抵消因较大定义域的分类变量引起的误差,信息增益率如(2.7)式所示:
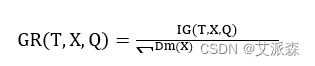
总体而言,决策树采用一种自上而下的分类策略,通过递归的方式遍历数据集的特征属性,并在每个节点选取分类性能最佳的属性进行分割,直到得到一个最佳的决策树模型。这个过程需要将数据集划分为训练集和测试集,对训练集用 CART 算法进行建模,得到分类规则,再用测试集对分类规则的性能进行评估,评估通过就可以对未知类型的数据进行分类预测。
(4)决策树的评价
决策树算法虽然简单好用,但存在着一些缺陷,主要有:(1)随着节点越来越多,树越来越深,某些叶子节点的记录会过少,得不出具有统计意义的规则;(2)子树可能重复出现过多次,使得决策树冗余又复杂,此时训练误差减小,但是测试误差开始增大,这就是典型的训练过度,造成模型过拟合。
2.3.2 朴素贝叶斯法
(1)算法简介
朴素贝叶斯法是基于贝叶斯定理与特征条件独立性假设的分类方法。对于给定的训练集,首先基于特征条件独立假设学习输入输出的联合概率分布(朴素贝叶斯法这种通过学习得到模型的机制,显然属于生成模型);然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。
(2)朴素贝叶斯分类器的公式
假设某个体有n项特征(Feature),分别为F1、F2、…、Fn。现有m个类别(Category),分别为C1、C2、…、Cm。贝叶斯分类器就是计算出概率最大的那个分类,也就是求下面这个算式的最大值:
P(C|F1F2...Fn) = P(F1F2...Fn|C)P(C)/P(F1F2...Fn)
由于P(F1F2…Fn) 对于所有的类别都是相同的,可以省略,问题就变成了求
P(F1F2...Fn|C)P(C)的最大值。朴素贝叶斯分类器则是更进一步,假设所有特征都彼此独立,因此
P(F1F2...Fn|C)P(C) = P(F1|C)P(F2|C) ... P(Fn|C)P(C)
上式等号右边的每一项,都可以从统计资料中得到,由此就可以计算出每个类别对应的概率,从而找出最大概率的那个类。虽然“所有特征彼此独立”这个假设,在现实中不太可能成立,但是它可以大大简化计算,而且有研究表明对分类结果的准确性影响不大。
(3)朴素贝叶斯常用的三个模型
高斯模型:处理特征是连续型变量的情况
多项式模型:最常见,要求特征是离散数据
伯努利模型:要求特征是离散的,且为布尔类型,即true和false,或者1和0
(4) 朴素贝叶斯法的评价
朴素贝叶斯法的优点:朴素贝叶斯算法假设了数据集属性之间是相互独立的,因此算法的逻辑性十分简单,并且算法较为稳定,当数据呈现不同的特点时,朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好,对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时,朴素贝叶斯分类算法会有较好的效果。
朴素贝叶斯法的缺点:属性独立性的条件同时也是朴素贝叶斯分类器的不足之处。数据集属性的独立性在很多情况下是很难满足的,因为数据集的属性之间往往都存在着相互关联,如果在分类过程中出现这种问题,会导致分类的效果大大降低。
2.3.3 KNN
(1)KNN算法简介
一提到KNN,很多人都想起了另外一个比较经典的聚类算法K_means,但其实,二者之间是有很多不同的,这两种算法之间的根本区别是,K_means本质上是无监督学习而KNN是监督学习,Kmeans是聚类算法而KNN是分类(或回归)算法。
古语说得好,物以类聚,人以群分;近朱者赤,近墨者黑。这两句话的大概意思就是,你周围大部分朋友是什么人,那么你大概率也就是这种人,这句话其实也就是KNN算法的核心思想。
(2)KNN算法的关键
①样本的所有特征都要做可比较的量化
若是样本特征中存在非数值的类型,必须采取手段将其量化为数值。例如样本特征中包含颜色,可通过将颜色转换为灰度值来实现距离计算。
②样本特征要做归一化处理
样本有多个参数,每一个参数都有自己的定义域和取值范围,他们对距离计算的影响不一样,如取值较大的影响力会盖过取值较小的参数。所以样本参数必须做一些 scale 处理,最简单的方式就是所有特征的数值都采取归一化处置。
③需要一个距离函数以计算两个样本之间的距离
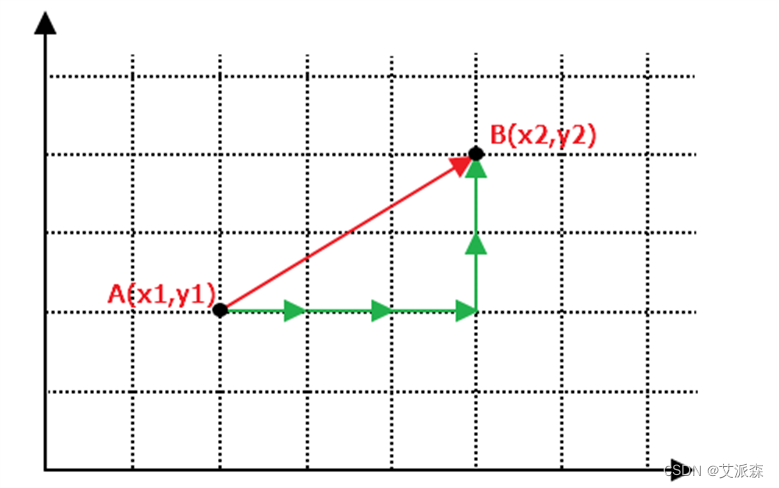
通常使用的距离函数有:欧氏距离、余弦距离、汉明距离、曼哈顿距离等,一般选欧氏距离作为距离度量,但是这是只适用于连续变量。在文本分类这种非连续变量情况下,汉明距离可以用来作为度量。通常情况下,如果运用一些特殊的算法来计算度量的话,K近邻分类精度可显著提高,如运用大边缘最近邻法或者近邻成分分析法。以计算二维空间中的A(x1,y1)、B(x2,y2)两点之间的距离为例,欧氏距离和曼哈顿距离的计算方法如下图所示:
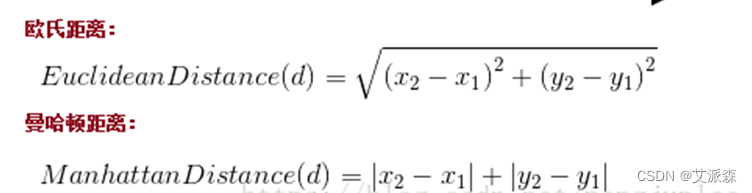
④确定K的值
K值选的太大易引起欠拟合,太小容易过拟合,需交叉验证确定K值。
KNN算法的优点:
1.简单,易于理解,易于实现,无需估计参数,无需训练;
2.适合对稀有事件进行分类;
3.特别适合于多分类问题(multi-modal,对象具有多个类别标签), kNN比SVM的表现要好。
KNN算法的缺点:
KNN算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数,如下图所示。该算法只计算最近的邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。可理解性差,无法给出像决策树那样的规则。
3、实验步骤
3.1导入模块和数据
1、在进行实验前先导入本次实验所需的所有模块。
2、导入本次实验的数据集,并进行基本的数据描述:数据大小、显示数据前十行、数据类型、数据的描述、统计缺失值数目。

显示结果如下:
(1)、数据大小
(7999,52)
(2)、显示数据前十行
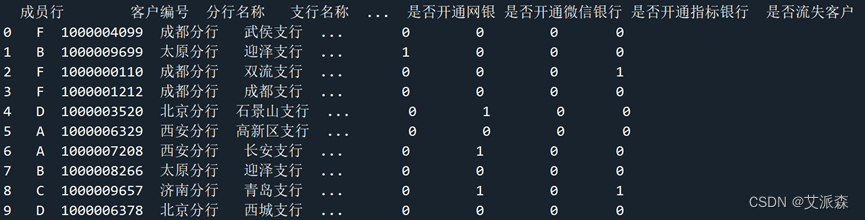
(3)、数据类型及统计缺失值
由于前文数据属性介绍已做详细展示,此处只展示部分运行结果。
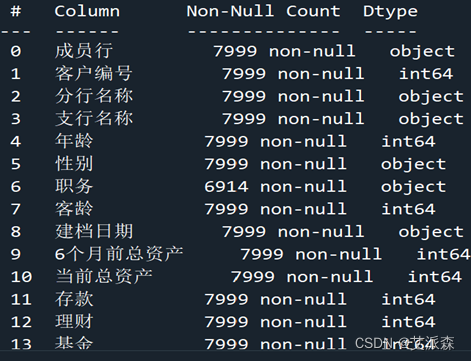
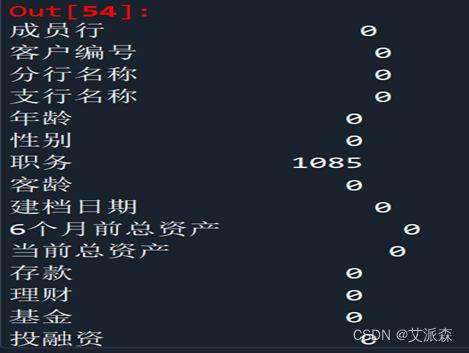
在职务、代发工资金额、代发工资标识均有不同数量的缺失值,后期数据预处理时需对缺失值作处理。
(4)、数据描述
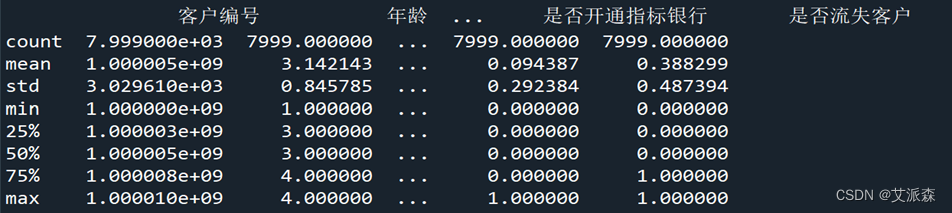
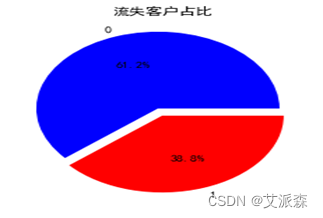
3、流失客户占比可视化

由图可以看出流失客户占比达到38.8%,如果能够成功预测客户流失,并及时采取措施挽留,将极大地提升银行的利润。同时由于此数据集中流失客户占比偏高,用来预测客户是否会流失会更加简单、准确。
3.2特征工程
3.2.1特征工程介绍
特征工程(Feature Engineering)特征工程是将原始数据转化成为更好地表达问题本质的特征的过程,使得将这些特征运用到预测模型中能提高对不可见数据的模型预测精度。
特征工程简单讲就是发现对因变量y有明显影响作用的特征,通常称自变量x为特征,特征工程的目的是发现重要特征。
3.2.2数据预处理
1、缺失值处理

由数据描述可知数据集中职务、代发工资标识、代发工资金额三列有缺失值,其中,代发工资标识和代发工资金额两列有关联且缺失数据多,采取直接删去的方式,而由于职务列缺失值少,且与因变量(是否流失客户)有较强的关联,不适合直接删除。职务列缺失值填充也没有合适的方法,所以采取了仅删除职务列有缺失的行的方式。
2、删去一些明显无关的变量(如:支行名称、分行名称、成员行、客户编号、建档日期)

3、属性变换
数据属性描述中提出:成员行、分行名称、支行名称、性别、职务、建档日期都为字符型数据,需要进行属性变换,经过数据预处理还剩下性别、职务列需要转换。
- 对性别列的变换
为便于后期处理,对性别列‘男’、‘女’变换为‘1’、‘0’。
 对职务列的变换
对职务列的变换
用pd.get_dummies处理职务列数据

pd.get_dummies函数简介:将分类变量转为哑变量,适用于离散特征的取值之间没有大小意义的变量处理。处理结果如下:
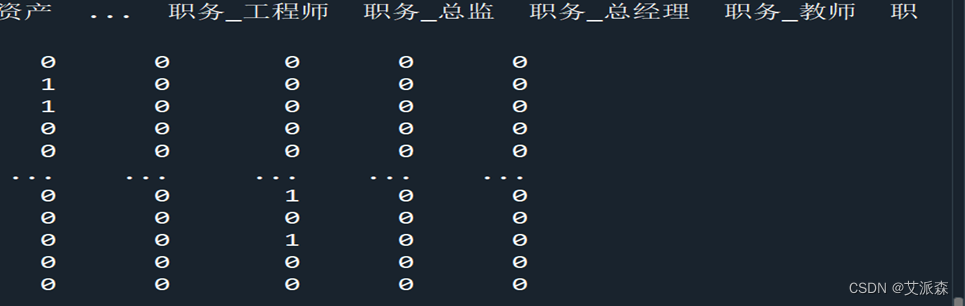
3.2.3特征选择
由于在一个数据集中不是所有的特征都是平等的,那些与问题不相关的属性需要被删除;还有一些特征可以比其他特征更重要;也有的特征跟其他的特征是冗余的。特征选择就是自动地选择对于问题最重要的特征的一个子集。它的作用有:①、简化模型,增加模型的可解释性;②、缩短训练时间;③、避免维度灾难;④、改善模型通用性、降低过拟合。
根据特征选择的形式可以将特征选择方法分为3种:
1.Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
优点:算法的通用性强;省去了分类器的训练步骤,算法复杂性低,因而适用于大规模数据集;可以快速去除大量不相关的特征,作为特征的预筛选器非常合适。
缺点:由于算法的评价标准独立于特定的学习算法,所选的特征子集在分类准确率方面通常低于Wrapper方法。
2.Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
优点:相对于Filter方法,Wrapper方法找到的特征子集分类性能通常更好。
缺点:Wrapper方法选出的特征通用性不强,当改变学习算法时,需要针对该学习算法重新进行特征选择;算法计算复杂度很高,尤其对于大规模数据集来说,算法的执行时间很长。
3.Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
优点:效果好速度快。
缺点:模式单调,,但是如何设置参数,需要深厚的背景知识。
由于本次实验需要采用KNN算法、朴素贝叶斯、决策树三种算法而且数据集涉及的特征众多,所以需要用算法适用性强的Filter方法对特征进行选择。
- 依据相关性初步筛选出15个特征
由于本数据集特征众多,含有大量不相关、冗余、相关性低的特征,通过相关系数计算、排序、筛选出前15个相关系数高的特征,并绘制出相关系数散点图。
得出的前15个相关系数高的特征分别为:['是否流失客户', '6个月前总资产', '当前总资产', '存款', '年龄', '基金', '职务_学生', '职务_警察', '职务_医生', '职务_教师', '理财', '投融资', '本月累计付款金额', '线下渠道付款金额', '本月累计交易金额', '其中柜面付款金额']
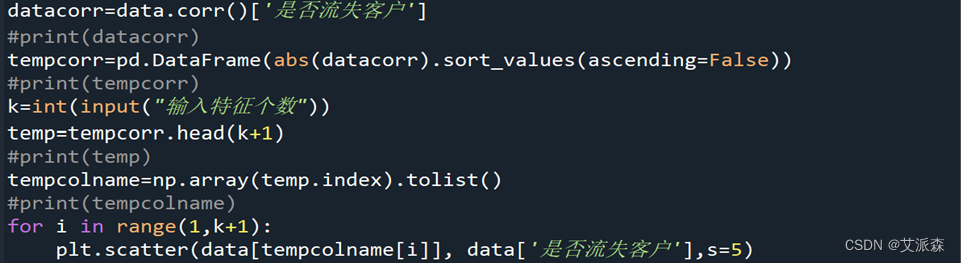
由散点图可知筛出的15个特征与‘是否流失客户’相关性并不强,需要进一步处理。
2.运用热力图分析各变量间的相关性
运行下列代码绘制15个变量的热力图
热力图如下:
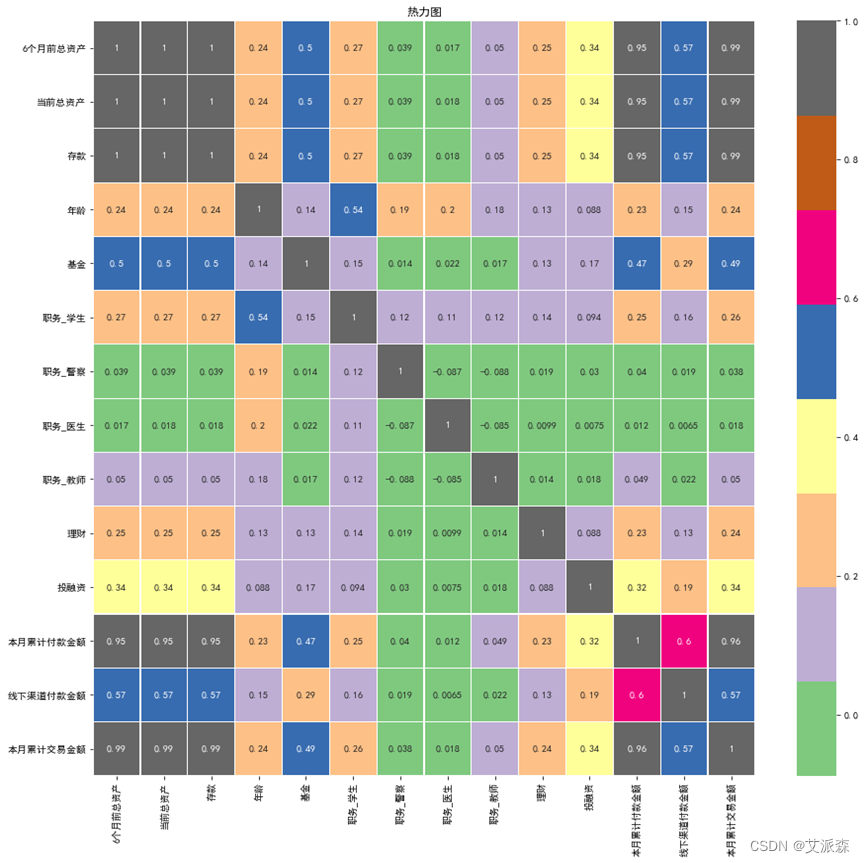
图中颜色越深表示相关性越强,由热力图分析可知:‘当前总资产’与‘六月前总资产’、‘存款’、‘本月累计付款金额’、‘本月累计交易金额’之间存在强正相关;‘线下渠道付款金额’与‘本月累计付款金额’之间也存在较强的正相关;‘基金’与‘6月前总资产’、‘当前总资产’、‘存款’、‘投融资’、‘本月累计交易金额’存在中正相关。
3、绘制相关系数柱状图分析各变量与‘是否流失客户’间的关联程度


由相关系数柱状图分析可以看出:‘本月累计付款金额'、'线下渠道付款金额'、'本月累计交易金额'、'其中柜面付款金额'与’是否流失客户‘的相关性低,表明这四个变量对电信企业客户流失的影响特别小,在后续进行预测研究时,不予考虑,采取直接删除的方式。
3.3数据可视化
运行代码,对流失客户和非流失客户的同一特征进行统计,为绘制柱状堆叠图作准备。
 3.3.1对职务分布可视化
3.3.1对职务分布可视化
运行以下代码来绘制各职务特征与是否流失客户之间的堆叠柱状图以探究他们之间是否存在潜在联系。绘图结果如下:
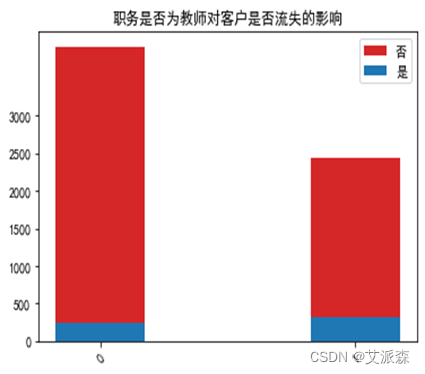
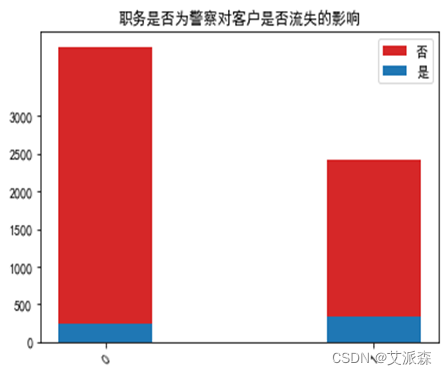
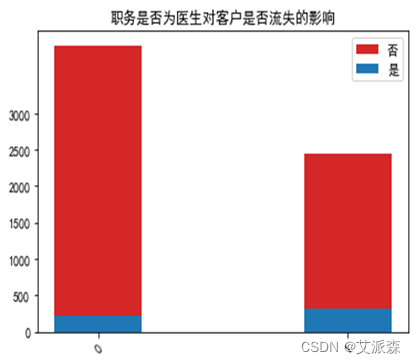
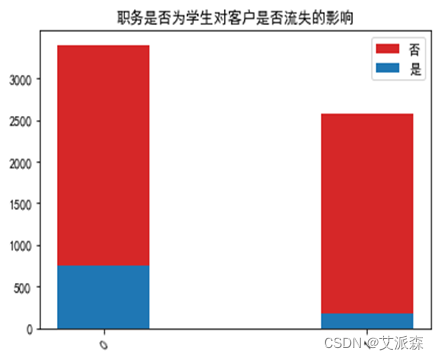
由图可以看出:医生、教师、警察这类较稳定的职业的客户流失人数较非流失人数更多一些,而学生这类不太稳定的职业流失人数会更少了。
3.3.2对年龄分布可视化
运行以下代码来绘制年龄特征与是否流失客户之间的堆叠柱状图以探究他们之间是否存在潜在联系。绘图结果如下:

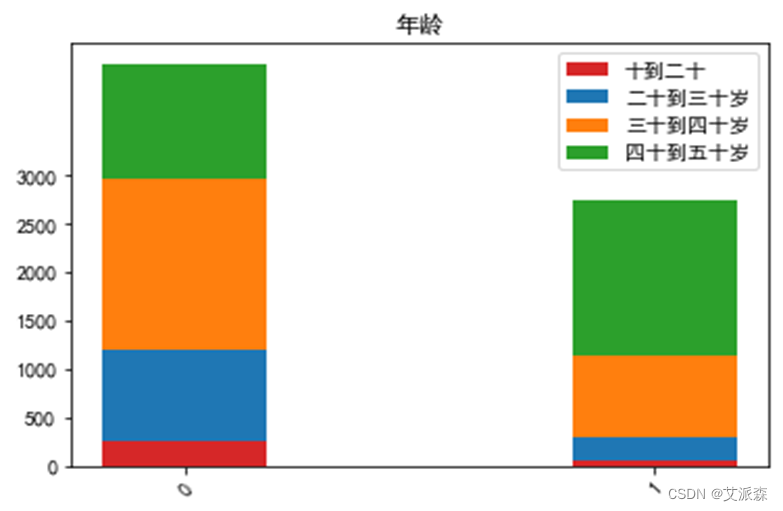
由图可以看出随着年龄的增长流失客户占比逐步增多,可见年龄对‘是否流失客户’有着一定的影响。
3.4模型构建
3.4.1拆分训练集测试集
数据拆分前,先将‘是否流失客户’列赋予Y,删去‘是否流失客户’列并将其他特征全部赋予X。
拆分的训练集占70%,测试集占30%,shuffle=True在数据进行划分前对数据集洗牌,random_state=None是为了保证程序每次运行程序数据集都能够随机分割。
运行下列代码划分训练集和测试集:
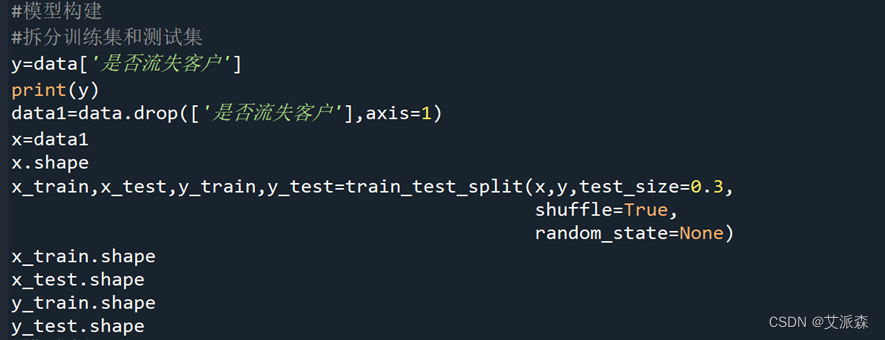
拆分后训练集测试集大小分别为:
| 数据集 | shape |
| x_train | (4839, 11) |
| y_train | (4839, 1 ) |
| x_test | (2075, 11) |
| y_tese | (2075, 1 ) |
3.4.2导入并拟合模型
运行下列代码,导入‘KNN’、‘朴素贝叶斯’、‘决策树’三种算法:
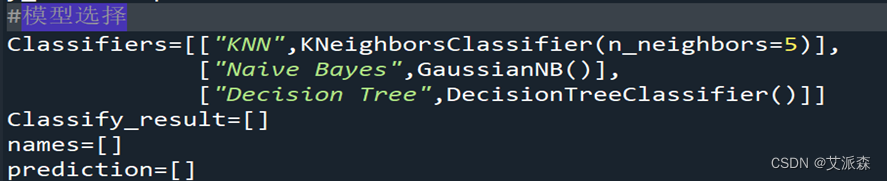
运行下列代码,拟合模型并导出预测结果及召回率和精确率:
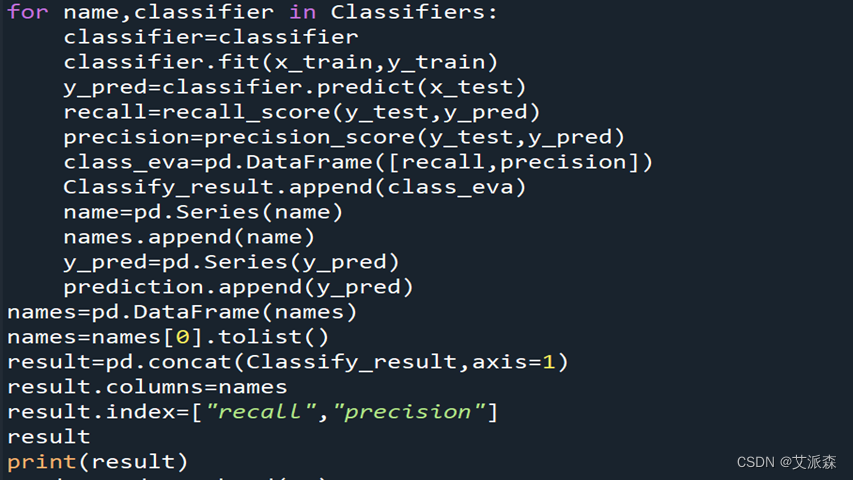
3.5模型评估
3.5.1 Recall和Precision评估
本次实验,我们运用了召回率(recall)和精确率(precision)来评估我们的模型。首先我们先了解一下什么是召回率和精确率。
召回率(recall):是针对我们原来样本而言,表示有多少样本中的正例(一种是把正类预测为正类即TP,一种是把正类预测为负类即FN)被预测正确了。R=TP/(TP+FN)提取出的正确信息条数/样本中的信息条数。
精确率(precision):是针对我们的预测结果而言,表示的是预测为正的样本中(一种是把正类预测为正类即TP,一种是把负类预测为正类即FP)有多少是真正的正样本。P=TP/(TP+FP)提取出的正确信息条数/提取出的信息条数。
其中TP:样本为正,预测结果为正;
FP:样本为负,预测结果为正;
TN:样本为负,预测结果为负;
FN:样本为正,预测结果为负。
一般来说,准确率和召回率反映了分类器性能的两个方面,单一依靠某个指标并不能较为全面地评价一个分类器的性能。想要全面评估模型的有效性,必须同时检验精确率和召回率。一般的,召回率和精确率往往是此消彼长,也就是说,提升精确率通常会降低召回率,反之亦然。只有在召回率和精确率都较高时模型的预测效果才较好。
运行下列代码对三种算法进行预测:
运行下列模型绘制混淆矩阵:

多次运行以上的代码得到的某次结果整理所得的混淆矩阵如下表。在2075个测试集样本中TP有1225个,TN有20个,FP有18个,FN有812个,预测效果良好。
| Actual Class | |||
| Predicted Class | Positive | Negative | |
| True | 1225 | 20 | |
| False | 18 | 812 | |
选取前五次运行结果展示如下表。由表可以看出,朴素贝叶斯的预测结果召回率偏低,表明在样本标注时多数正样本被错误的标注为负样本,模型的标注正例的能力较弱。KNN,决策树这两种算法对该数据集预测结果的召回率和精确率都较高,效果良好,其中KNN预测效果较决策树更优,表明KNN算法更适合该数据集。
| 实验次数 | 预测指标 | KNN | Naive Bayes | Decision Tree |
| 1 | recall | 0.984906 | 0.750943 | 0.979874 |
| precision | 0.979975 | 0.967585 | 0.979874 | |
| 2 | recall | 0.977415 | 0.74404 | 0.984944 |
| precision | 0.979874 | 0.94880 | 0.976368 | |
| 3 | recall | 0.971848 | 0.755202 | 0.985312 |
| precision | 0.977833 | 0.968603 | 0.982906 | |
| 4 | recall | 0.976048 | 0.754491 | 0.974850 |
| precision | 0.974850 | 0.966258 | 0.972521 | |
| 5 | recall | 0.975352 | 0.737089 | 0.973005 |
| precision | 0.985765 | 0.970634 | 0.982227 |
3.5.2 ROC曲线评估
ROC曲线:接收者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,ROC曲线上每个点反映着对同一信号刺激的感受性。
横坐标:1-Specificity,假正类率(False positive rate,FPR,FPR=FP/(FP+TN)),预测为正但实际为负的样本占所有负例样本的比例;
纵坐标:Sensitivity,真正类率(True positive rate,TPR,TPR=TP/(TP+FN)),预测为正且实际为正的样本占所有正例样本的比例。
利用ROC曲线评估预测结果的理想情况,TPR应接近1,FPR接近0,即图中的(0,1)点。ROC曲线越靠拢(0,1)点,越偏离45度对角线越好。
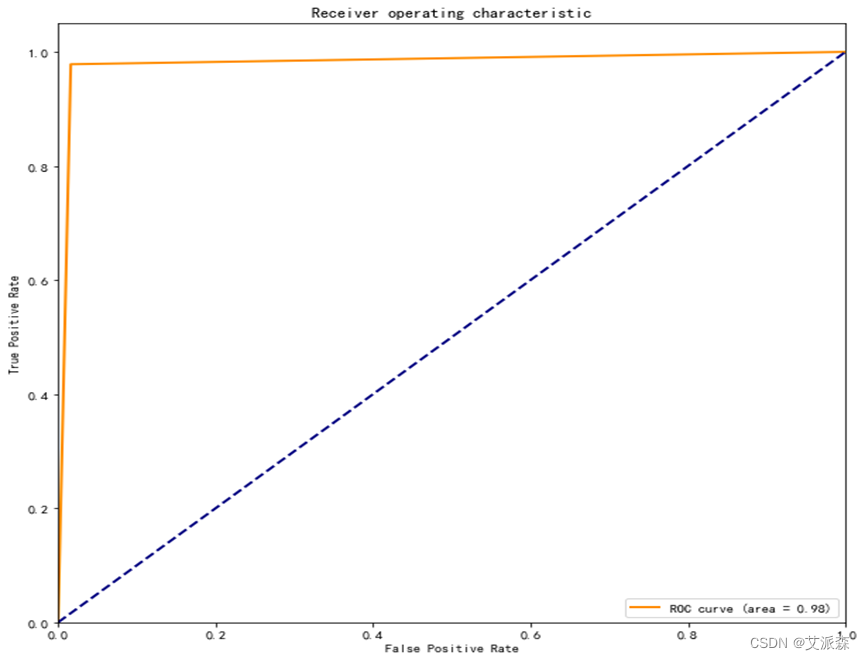
运行下列代码绘制ROC曲线:
绘制ROC曲线如下图,由图可以看出所画的roc曲线非常接近(0,1)点,曲线下方的面积接近1,可见模型预测的结果还是非常良好的。
4 实验总结
近年来,随着电子支付,互联网金融等行业的发展,实体银行的客户群体进一步缩小,为了避免客户大量流失,对影响客户流失的相关因素的数据分析就显得尤为重要。
本报告立足银行客户流失分析,通过客户是否流失数据,客户的基础信息,客户拥有的存款信息等为基础,综合考虑流失的特点和与之相关的多种因素,使用了相关性系数,特征工程,热力图等数据筛选及可视化的方法,寻找与客户流失密切相关的特征,如:6个月前总资产, 当前总资产, 存款, 年龄, 基金, 职务_学生, 职务_警察, 职务_医生, 职务_教师, 理财, 投融资等。并在此基础上使用了KNN,朴素贝叶斯,决策树三个数据分析模型,分别对客户流失的影响因子进行了比较分析,在数据预测精确率和召回率高达90%的决策树模型中得出了本次实验的结果,表明了在分析特征过程中可以大概率预测准确客户的流失。例如年龄和流失与否的关系,可以看出拥有较为稳定职业的不容易流失;以及不同年龄分布占流失客户和留存客户的比例,中青年人相对更容易成为目标客户群体;六个月前总资产也与流失与否产生重要影响。因此,根据实验结果,要想降低银行客户的流失率,可以针对具有某些特征的人群制定相应的营销策略,采取针对性措施,从而达到挽留客户的目的:针对那些职业流动性较大的人群制定相应的理财方案;对于存款贡献率较大的中青年更优质的服务;以及六个月以内存款超过一定数额的客户及时沟通与维护。在经营的过程中进行全方位思考,不能等到客户流失之时再追悔莫及。只有这样才能从根源上避免客户流失带来的各种各样的损失。随着互联网技术的飞速发展,带来的是大量数据在日常生活中产生,如何巧妙合理地利用这些数据,提取有用的信息是我们值得思考的问题。在本次实验的过程中,通过对银行客户实际数据的分析,对大数据分析与应用有了初步的了解,也为以后更深层次的学习奠定了基础。
通过这次Python项目实战,我学到了许多新的知识,这是一个让我把书本上的理论知识运用于实践中的好机会。原先,学的时候感叹学的资料太难懂,此刻想来,有些其实并不难,关键在于理解。在这次实战中还锻炼了我其他方面的潜力,提高了我的综合素质。首先,它锻炼了我做项目的潜力,提高了独立思考问题、自我动手操作的潜力,在工作的过程中,复习了以前学习过的知识,并掌握了一些应用知识的技巧等
在此次实战中,我还学会了下面几点工作学习心态:
1)继续学习,不断提升理论涵养。在信息时代,学习是不断地汲取新信息,获得事业进步的动力。作为一名青年学子更就应把学习作为持续工作用心性的重要途径。走上工作岗位后,我会用心响应单位号召,结合工作实际,不断学习理论、业务知识和社会知识,用先进的理论武装头脑,用精良的业务知识提升潜力,以广博的社会知识拓展视野。
2)努力实践,自觉进行主角转化。只有将理论付诸于实践才能实现理论自身的价值,也只有将理论付诸于实践才能使理论得以检验。同样,一个人的价值也是透过实践活动来实现的,也只有透过实践才能锻炼人的品质,彰显人的意志。
3)提高工作用心性和主动性。实习,是开端也是结束。展此刻自我面前的是一片任自我驰骋的沃土,也分明感受到了沉甸甸的职责。在今后的工作和生活中,我将继续学习,深入实践,不断提升自我,努力创造业绩,继续创造更多的价值。
这次Python实战不仅仅使我学到了知识,丰富了经验。也帮忙我缩小了实践和理论的差距。在未来的工作中我会把学到的理论知识和实践经验不断的应用到实际工作中,为实现理想而努力。
源代码
#导入相应模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.preprocessing import StandardScaler
import matplotlib as mpl
import seaborn as sns
from pylab import rcParams
import matplotlib.cm as cm
%matplotlib inline
import csv
import warnings
from numpy import newaxis
import sklearn
from sklearn import preprocessing
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report, precision_score, recall_score
from sklearn.metrics import confusion_matrix
#导入数据
data=pd.read_csv(r"C:\Users130/Documents/Tencent Files/3324339399/FileRecv/train.csv")
print(data)
#描述数据特征
print(data.head(10))#描述前十行
print(data.info())#数据相关信息
data.isnull().sum()
plt.rcParams['font.sans-serif'] = ['SimHei'] #解决中文显示问题
plt.rcParams['axes.unicode_minus'] = False # 解决中文显示问题
churnvalue=data['是否流失客户'].value_counts()
labels=data['是否流失客户'].value_counts().index
plt.pie(churnvalue,labels=labels,colors=['blue','red'],
explode=(0.1,0),autopct='%1.1f%%')
plt.title('流失客户占比')
plt.show
dataname=data['客户编号']
#特征工程
data=data.drop(['支行名称','分行名称','成员行','客户编号'],axis=1)
genger1={'男':1,'女':0}
data["性别"]=data["性别"].map(genger1)
data=data.drop(['代发工资标识','代发工资金额','建档日期'],axis=1)
data=data.dropna(axis=0)
data=pd.get_dummies(data,columns=["职务"])
print(data)
datacorr=data.corr()['是否流失客户']
#print(datacorr)
tempcorr=pd.DataFrame(abs(datacorr).sort_values(ascending=False))
#print(tempcorr)
k=int(input("输入特征个数"))
temp=tempcorr.head(k+1)
#print(temp)
tempcolname=np.array(temp.index).tolist()
print(tempcolname)
for i in range(1,k+1):
plt.scatter(data[tempcolname[i]], data['是否流失客户'],s=50)
plt.title("相关系数散点图")
#print(data.info())
data = data[tempcolname]
#print(data)
charges=data.iloc[:,1:15]
corrDf = charges.apply(lambda x: pd.factorize(x)[0])
corrDf .head()
#print(corrDf .head)
corr = corrDf.corr()
#print(corr)
plt.figure(figsize=(15,15))
ax = sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns,
linewidths=0.2, cmap="Accent",annot=True)
plt.title("热力图")
plt.show()
plt.figure(figsize=(15,15))
data.corr()['是否流失客户'].sort_values(ascending = False).plot(kind='bar')
plt.title("各变量对客户是否流失的影响")
plt.show()
data=data.drop(['本月累计付款金额', '线下渠道付款金额',
'本月累计交易金额', '其中柜面付款金额'],axis=1)
data.describe()
print(data.info())
plt.figure(figsize=(6,6))
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
Age = data['年龄']
Nb=data['是否流失客户']
plt.plot(Age,Nb,'o')
plt.xlabel('年龄')
plt.ylabel('流失状况')
plt.show()
data.shape
data.head()
data.describe()
#可视化处理
#统计结果
data_gender = data[['是否流失客户', '6个月前总资产', '当前总资产',
'存款', '年龄', '基金', '职务_学生', '职务_警察',
'职务_医生', '职务_教师', '理财', '投融资']]
print(data_gender)
data_gender_re = data_gender[data_gender.notnull()]
def count(data,X):
tj = data[X]
tq = data['是否流失客户']
xs = list(set(tj))
ys = list(set(tq))
D =[]
for y in ys:
PP = data_gender_re.loc[(data_gender_re['是否流失客户'] == y)]
PPN = PP[X]
cnt=[]
for x in xs:
m = 0
for value in PPN:
if value == x :
m = m+1
cnt.append(m)
cnt = np.array(cnt)
D.append(cnt)
D=np.array(D)
return xs,ys,D
#职务影响可视化
[xs,ys,D]=count(data,'职务_医生')
Female=D[:,0]
Male=D[:,1]
ind = np.arange(2)
width = 0.35
p1 = plt.bar(ind, Female, width, color='#d62728')
p2 = plt.bar(ind, Male, width, bottom=1)
plt.title('职务是否为医生对客户是否流失的影响')
plt.xticks(ind, ('0','1'),rotation=45)
plt.yticks(np.arange(0, 3500, 500))
plt.legend((p1[0], p2[0]), ('否', '是'))
plt.show()
[xs,ys,D]=count(data,'职务_学生')
Female=D[:,0]
Male=D[:,1]
ind = np.arange(2)
width = 0.35
p1 = plt.bar(ind, Female, width, color='#d62728')
p2 = plt.bar(ind, Male, width, bottom=1)
plt.title('职务是否为学生对客户是否流失的影响')
plt.xticks(ind, ('0','1'),rotation=45)
plt.yticks(np.arange(0, 3500, 500))
plt.legend((p1[0], p2[0]), ('否', '是'))
plt.show()
[xs,ys,D]=count(data,'职务_教师')
Female=D[:,0]
Male=D[:,1]
ind = np.arange(2)
width = 0.35
p1 = plt.bar(ind, Female, width, color='#d62728')
p2 = plt.bar(ind, Male, width, bottom=1)
plt.title('职务是否为教师对客户是否流失的影响')
plt.xticks(ind, ('0','1'),rotation=45)
plt.yticks(np.arange(0, 3500, 500))
plt.legend((p1[0], p2[0]), ('否', '是'))
plt.show()
[xs,ys,D]=count(data,'职务_警察')
Female=D[:,0]
Male=D[:,1]
ind = np.arange(2)
width = 0.35
p1 = plt.bar(ind, Female, width, color='#d62728')
p2 = plt.bar(ind, Male, width, bottom=1)
plt.title('职务是否为警察对客户是否流失的影响')
plt.xticks(ind, ('0','1'),rotation=45)
plt.yticks(np.arange(0, 3500, 500))
plt.legend((p1[0], p2[0]), ('否', '是'))
plt.show()
#年龄的影响
[xs,ys,D]=count(data,'年龄')
Female=D[:,0]
Male=D[:,1]
Female1=D[:,2]
Male2=D[:,3]
ind = np.arange(2)
d = []
for i in range(0,2):
sum = Female[i] + Male[i]
d.append(sum)
d1 = []
for i in range(0,2):
sum = Female[i] + Male[i] + Female1[i]
d1.append(sum)
width = 0.35
p1 = plt.bar(ind, Female, width, color='#d62728')
p2 = plt.bar(ind, Male, width, bottom=Female)
p3 = plt.bar(ind, Female1, width, bottom=d)
p4 = plt.bar(ind, Male2, width, bottom=d1)
plt.title('年龄')
plt.xticks(ind, ('0','1'),rotation=45)
plt.yticks(np.arange(0, 3500, 500))
plt.legend((p1[0],p2[0],p3[0],p4[0]),('十到二十', '二十到三十岁',
'三十到四十岁', '四十到五十岁'))
plt.show()
#模型构建
#拆分训练集和测试集
y=data['是否流失客户']
print(y)
data1=data.drop(['是否流失客户'],axis=1)
x=data1
x.shape
x_train,x_test,y_train,y_test=train_test_split(x,y,
test_size=0.3,
shuffle=True,
random_state=None)
x_train.shape
x_test.shape
y_train.shape
y_test.shape
#模型评估
Classifiers=[["KNN",KNeighborsClassifier(n_neighbors=5)],
["Naive Bayes",GaussianNB()],
["Decision Tree",DecisionTreeClassifier()]]
Classify_result=[]
names=[]
prediction=[]
for name,classifier in Classifiers:
classifier=classifier
classifier.fit(x_train,y_train)
y_pred=classifier.predict(x_test)
recall=recall_score(y_test,y_pred)
precision=precision_score(y_test,y_pred)
class_eva=pd.DataFrame([recall,precision])
Classify_result.append(class_eva)
name=pd.Series(name)
names.append(name)
y_pred=pd.Series(y_pred)
prediction.append(y_pred)
names=pd.DataFrame(names)
names=names[0].tolist()
result=pd.concat(Classify_result,axis=1)
result.columns=names
result.index=["recall","precision"]
result
print(result)
#绘制混淆矩阵
from sklearn.metrics import confusion_matrix
from sklearn.metrics import recall_score
a = confusion_matrix(y_test,y_pred)
print(a)
#绘制roc曲线
from sklearn.metrics import roc_curve, auc
# Compute ROC curve and ROC area for each class
fpr,tpr,threshold = roc_curve(y_test, y_pred) #计算真正率和假正率
roc_auc = auc(fpr,tpr) #计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) #假正率为横坐标,真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, line)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="lower right")
plt.show()














