✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅

✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨

🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿

🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟

🌟🌟 追风赶月莫停留 🌟🌟

🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀

🌟🌟 平芜尽处是春山🌟🌟

🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟

🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿

✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨

✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅

📝数据结构OJ题

• ✏️移除元素
• ✏️ 删除重复项
• ✏️ 合并两个数组

  ✏️移除元素

  

  题目链接：原地移除数组中所有的元素val，要求时间复杂度为O(N)，空间复杂度为O(1)

  我在这里给大家提供了常规的三种解法，第一种解法是错误示范

  解法一:大家首先肯定想到的是边遍历边删除，当然这也是常用的方法，但是实际上这个解法一是错误的

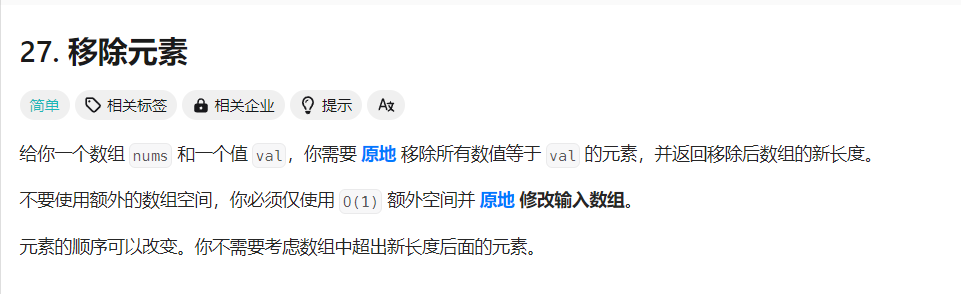
  int removeElement(int* nums, int numsSize, int val)
  {
      for (int i = 0; i < numsSize; i++)
      {
          if (nums[i] == val)
          {
              for (int j = i; j < numsSize - 1; j++)
              {
                  nums[j] = nums[j + 1];
              }
              numsSize--;
          }
      }
      for (int i = 0; i < numsSize; i++)
      {
          if (nums[i] == val)
          {
              for (int j = i; j < numsSize - 1; j++)
              {
                  nums[j] = nums[j + 1];
              }
              numsSize--;
          }
      }
      return numsSize;
  }
  

  大家可以看到在这里我用到了两次for循环进行遍历和删除而且是一模一样的，大家可以看下面的图：

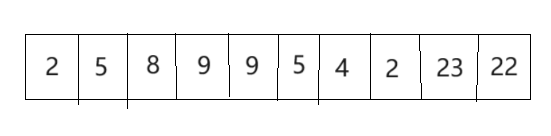
  会出现两个相邻的数是一样的，如果你把前面的那个9去除了，那么后面那个9就会移到前面那个数的位置，而此时那个位置已经检查过了，所以第二个9就没发删除，就会遗留下来：

  

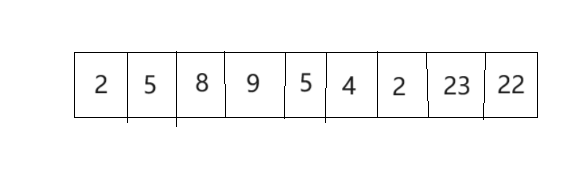
  所以这里就采用两次循环就可以解决，但是问题来了，如果是三个相邻的数相同，是不是就得用三个for循环，那如果是四个，五个呢，所以该解法错误的原因在这里。当然你也可以先找到最多有几个相同并且相邻的数的次数，然后再用for循环当然这也可以，但是太复杂了，大家还是看看解法二。

  解法二：该解法用了指针

  int removeElement(int* nums, int numsSize, int val)
  {
      int* ret = nums;//重新定义一个新的数组空间
      int sum = 0;
      while (numsSize)
      {
          if (*nums != val)
          {
              *ret++ = *nums++;   //把不同的数移到新的数组空间中
              sum++;                     //记录新数组的长度
          }
          else
          {
              nums++;
          }
          numsSize--;
      }
      return sum;
  }
  

  解法二是利用了指针，解法才变得简单起来。

  解法三：用了两个变量

  int removeElement(int* nums, int numsSize, int val) {
      int right = 0 ;
      int left  = 0 ;
      for (int i = 0; i < numsSize; i++)
      {
          if (nums[i] != val)
           {
              nums[left] = nums[right] ;
              left++;
              right++;
           }
          else
              right++;
      }
      return left;
  }
  

  在这里也是利用两个变量相互移动及赋值，不过这种解法教于指针更容易理解。

  ✏️ 删除重复项

  

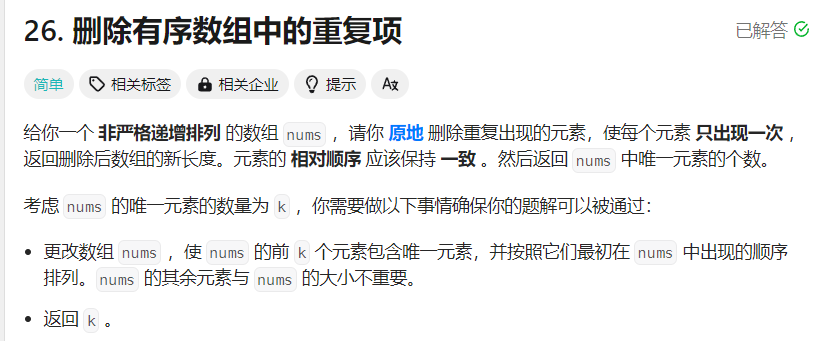
  题目链接： 删除排序数组中的重复项

  解法：

  int removeDuplicates(int* nums, int numsSize) {
      int left = 0 ;
      int right = 0 ;
      for(int i = 0; i < numsSize-1; i++)
      {
          if (nums[i] != nums[i+1])
          {
               left++;
               right++;
               nums[left] = nums[right] ;
          }
          else
          right++;
      }
      return left+1;
  }
  

  在这里还是利用了两个变量来记录数组元素的变化及移动，和上一题的解法三还是挺类似的，不过还是有一点差别。因为上一题我们是先赋值再移动，而这一题我们是先移动再赋值。为什么第二题就要先移动再赋值呢，这是因为我们这里是要保留一个，删除重复的，而第一题是直接删除。

  ✏️ 合并两个数组

  

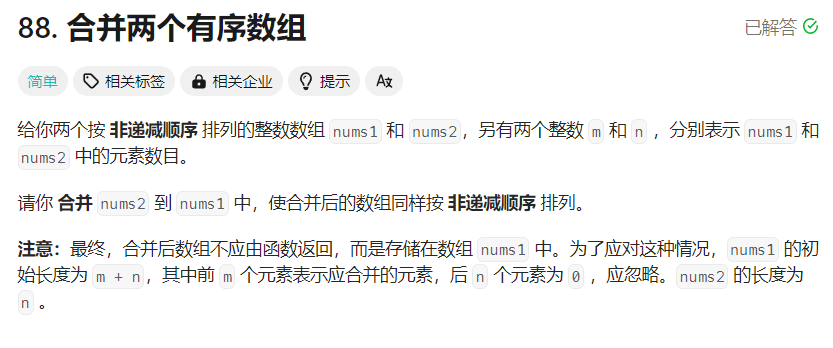
  题目链接： 合并两个有序数组

  解法：

  void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
       int m1 = m - 1 ;
       int n1 = n - 1 ;
       int sum = m + n - 1 ;
       while(m1>=0 && n1>=0)
       {
           if (nums1[m1] > nums2[n1])
           {
               nums1[sum] = nums1[m1] ;
               m1--;
               sum--;
           }
           else
           {
               nums1[sum] = nums2[n1] ;
              n1--;
              sum--;
           }
       }
       while(n1>=0)
       {
           nums1[sum] = nums2[n1] ;
           n1--;
           sum--;
       }
  }
  

  首先这一题无论是初始的两个数组还是后面合并的数组都是要求数据以递增的形式呈现。

  

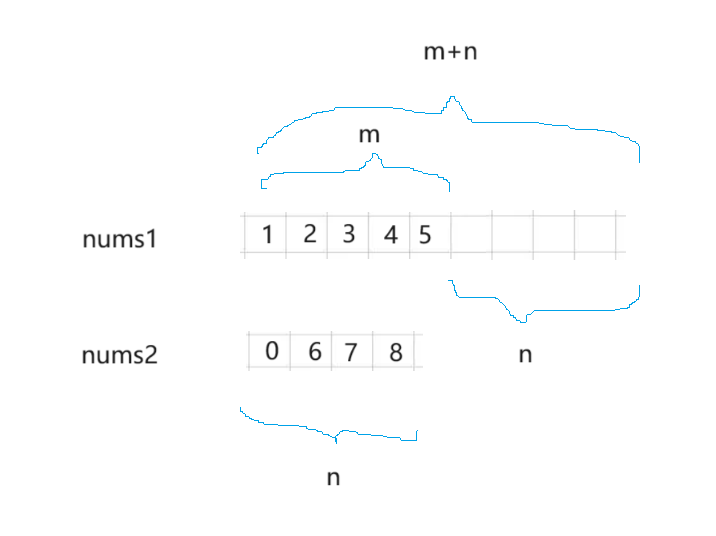
  上幅图中就是题目所给的两个有序数组和一些条件。

  按照题目意思我们只能从后面把数据填进去，如果从前面会覆盖一些数据，造成数据丢失。

  利用遍历来做，因为题目要求数据是递增的形式。所以只能利用遍历，一边遍历一边比大小。

  在这里又要分两种情况：

  第一种：n1还有剩余，m1已经分配完了，如下图所示

  

  

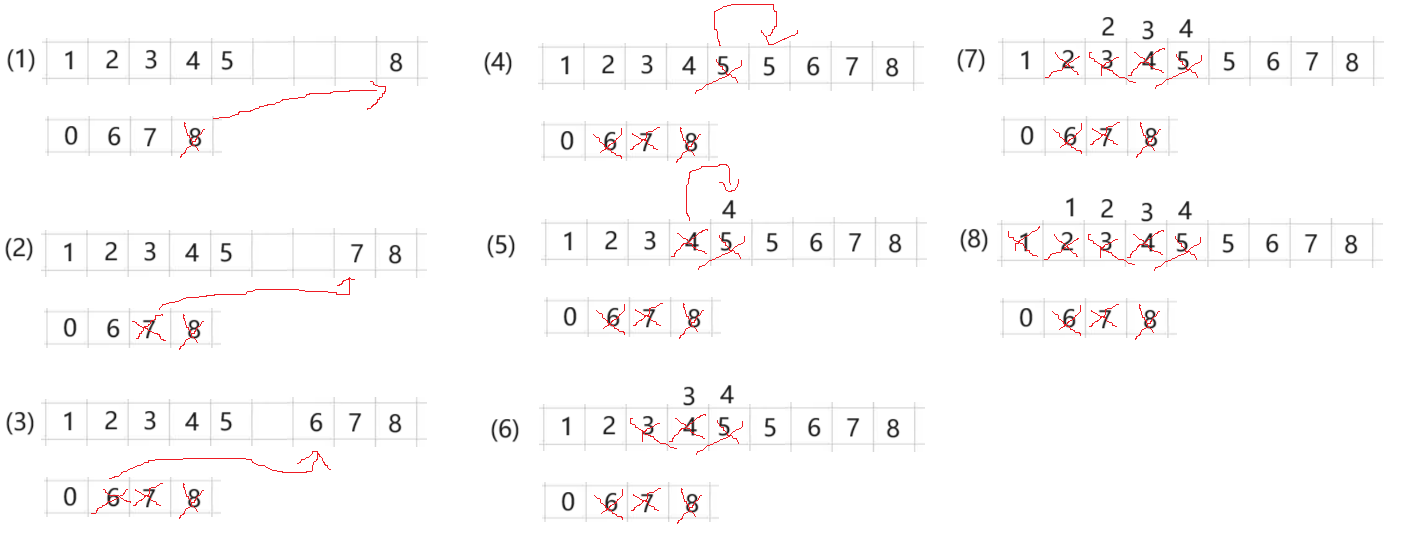
  在这里m1是已经为0了，所以会跳出循环，然后直接把nums2中剩余的数补到nums1的前面就可以了。

  第二种：m1还有剩余，n1已经分配完了，如下图所示

  

  

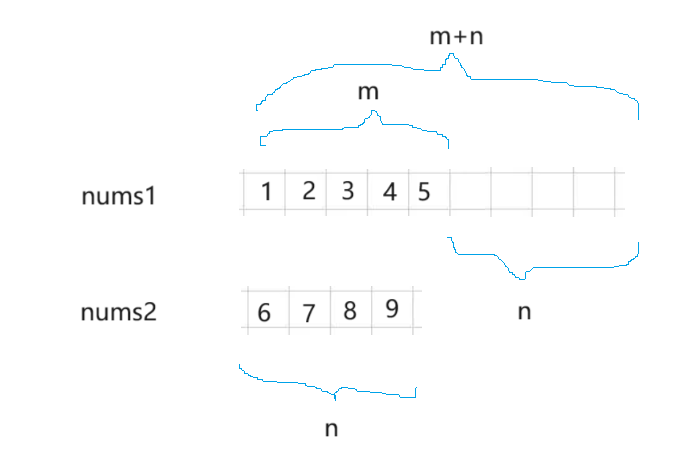
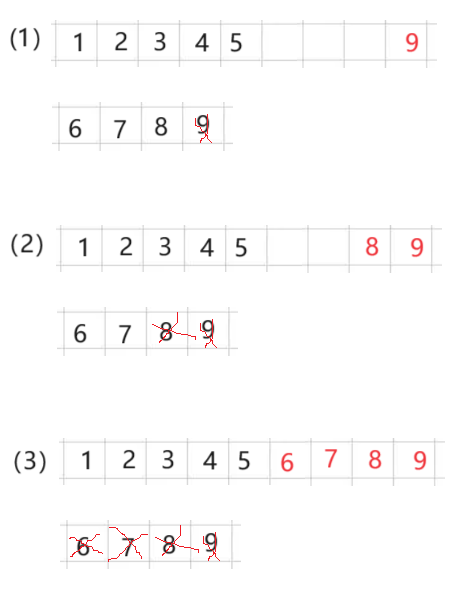
  像这种情况就可以直接结束了。

  知道这两种情况后，应该就能明白我们后面为什么会加一个循环，就是为了防止第一种情况的出现。

  

   
   搜索引擎优化简历  四川建设网项目招标  专门的网页制作软件  湖南网  建程网  网站定制公司哪家好