1、题目介绍

原题链接：287. 寻找重复数 - 力扣（LeetCode）

示例 1：

输入：nums = [1,3,4,2,2]
输出：2

示例 2：

输入：nums = [3,1,3,4,2]
输出：3

提示：

• 1 <= n <= 105
• nums.length == n + 1
• 1 <= nums[i] <= n
• nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

2、解题

2.1、解题思路

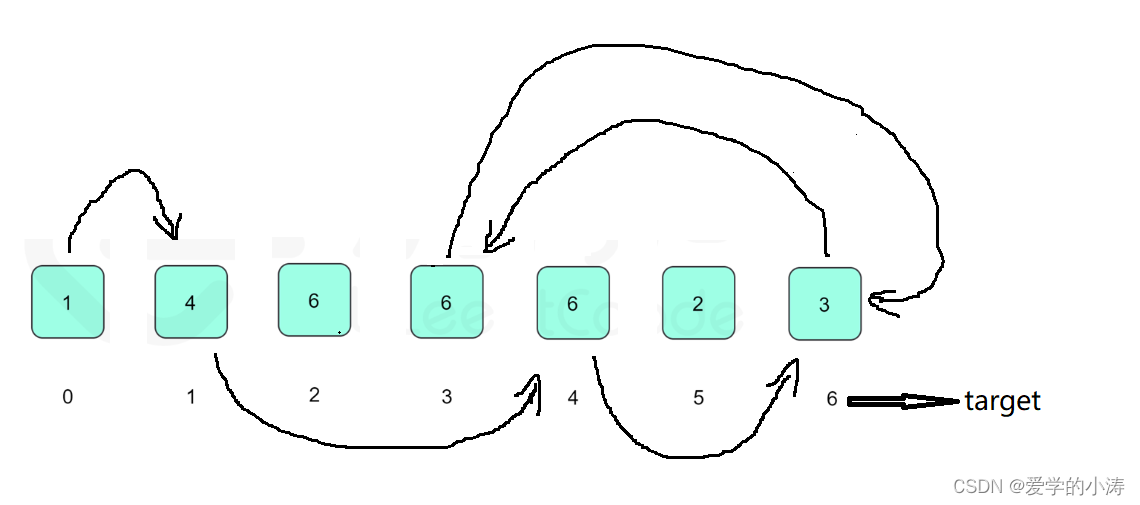
当我们用一个指针 i=0 以 i = nums[i]; 的方式遍历数组nums[ ]后可以得到图1，因为数组nums[ ]中一定存在的重复的数字 target，所以 target=( 6 ) 这个位置一定有起码两条指向它的边，因此整张图一定存在环，且我们要找到的 target就是这个环的入口，同时也是这道题的答案。用这种方法需要对「Floyd 判圈算法」有所了解。

「Floyd 判圈算法」（又称龟兔赛跑算法），可用于判定链表、迭代函数、有限状态机中是否有环。如果有环，可以找出环的起点，求出环的长度。 

基本思想：利用了快慢指针的思想。比如两个人在赛跑，A速度快，B速度慢，若是存在环(勺状图)，A和B总是会相遇的，相遇时A所经过的路径的长度要比B多若干个环的长度。

• 算法时间复杂度：令S到P的距离为m，环的长度为n，时间复杂度O(m+n）,即O(n);
• 空间复杂度：O(1);

图1： 

​ 

2.2、图解说明

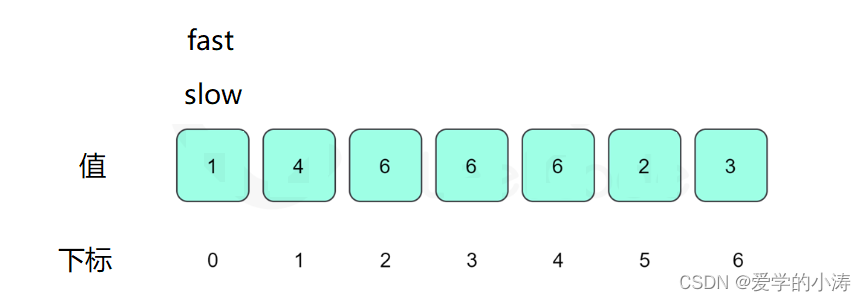
定义两个指针，分别是慢指针slow和快指针fast。

一开始让两个指针都指向下标0，然后两个指针每次指向的下一个下标为数组里当前下标的值，slow指针每次进行一次指向下一个下标的操作，fast指针每次进行两次指向下一个下标的操作；

即：slow = nums[ slow ] ;   fast = nums[ nums[ fast ] ] ;

然后判断slow 是否等于fast，即：while(slow != fast)

根据「Floyd 判圈算法」，两个指针在有环的情况下一定会相遇，所以当两个指针在环里面相遇的时候我们再将 slow指针 放置起点 0，两个指针每次同时移动一步，相遇的点就是答案（即环的入口）。

 ​​​​

​

​

​

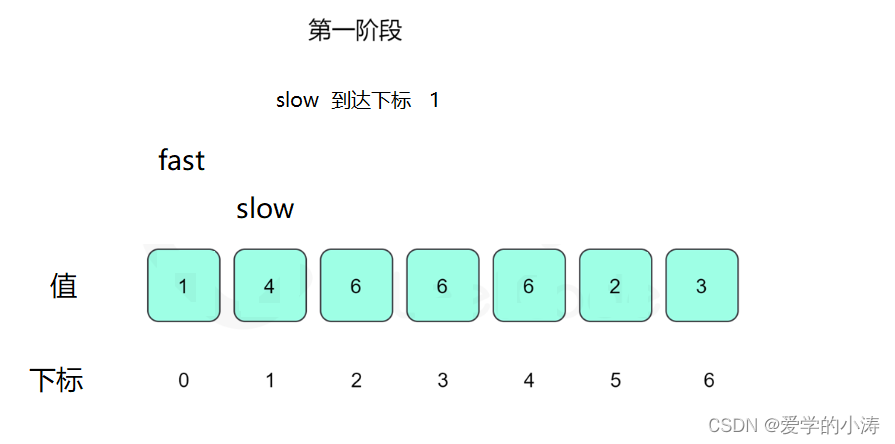
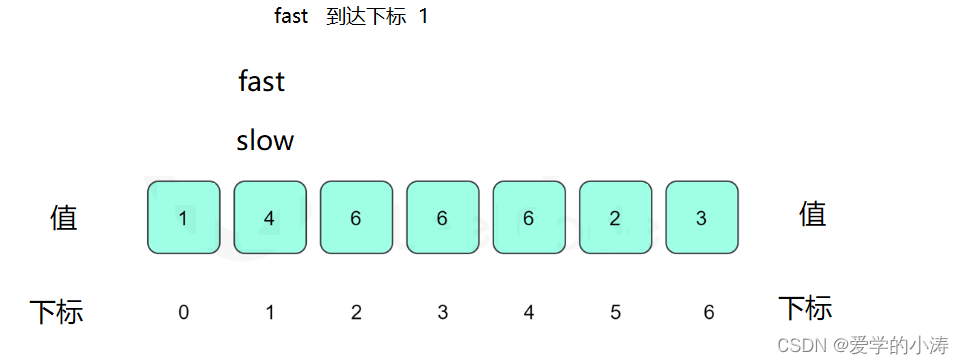
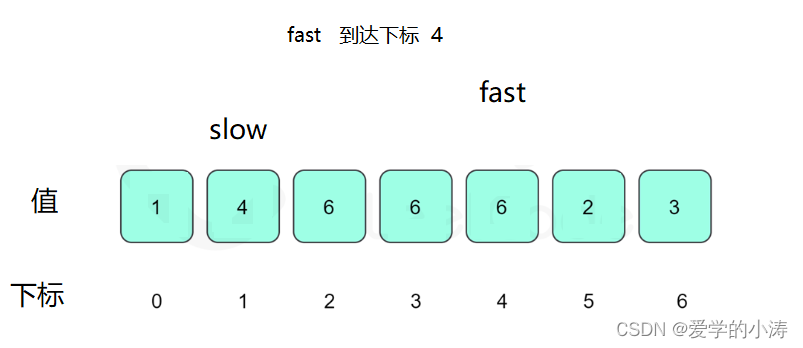
这时候让slow等于4，fast等于4然后fast再等于6，即：slow = nums[ slow ] ;   fast = nums[ nums[ fast ] ] ; 所以slow = 4 不等于fast = 6

​

​

​

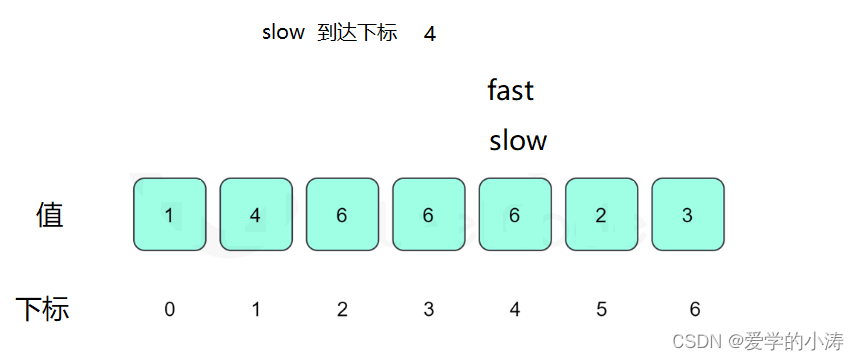
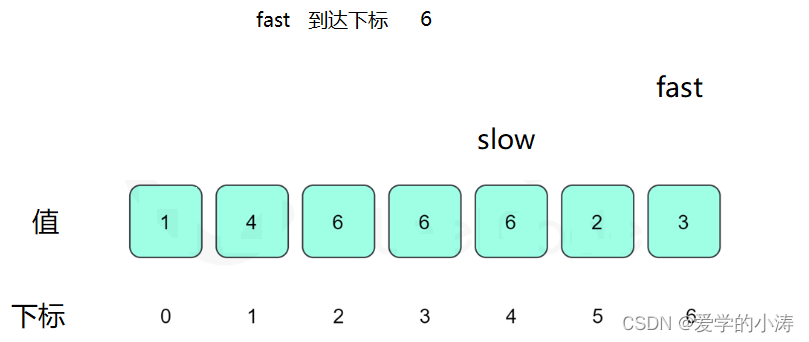
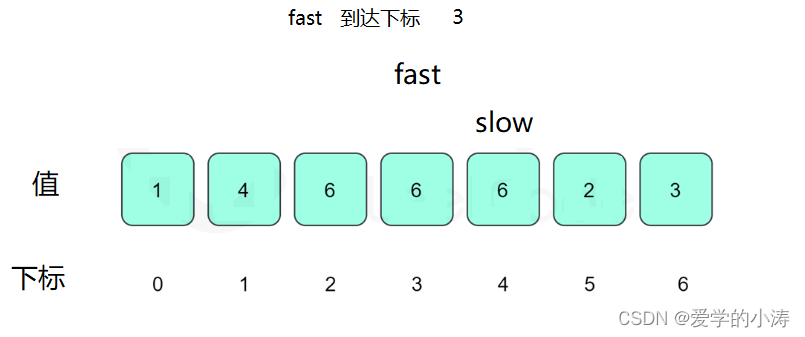
这时候让slow等于6，fast等于3然后fast再等于6，即：slow = nums[ slow ] ;   fast = nums[ nums[ fast ] ] ; 所以slow = 6 等于fast = 6

这时候我们将 slow指针放置起点 0，两个指针每次同时移动一步

​

​

​

​

​

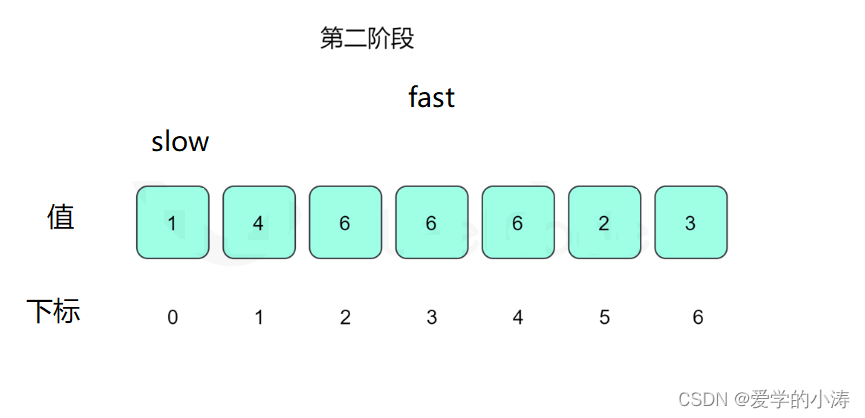
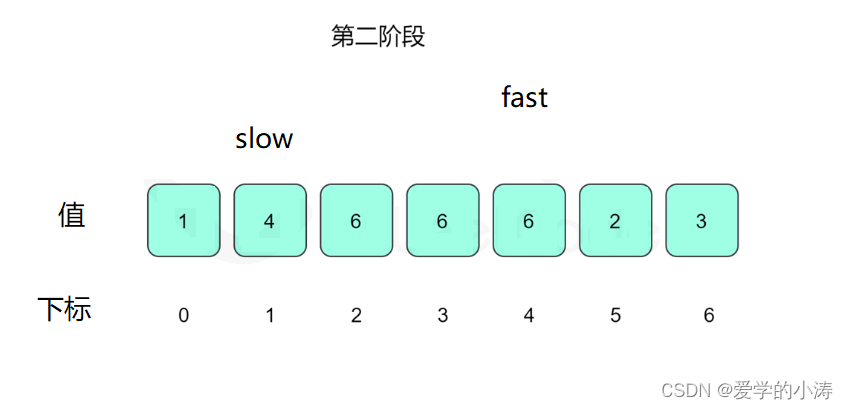
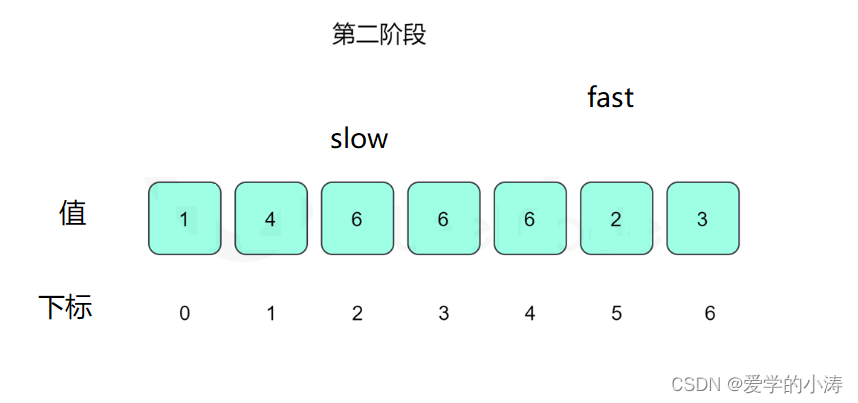
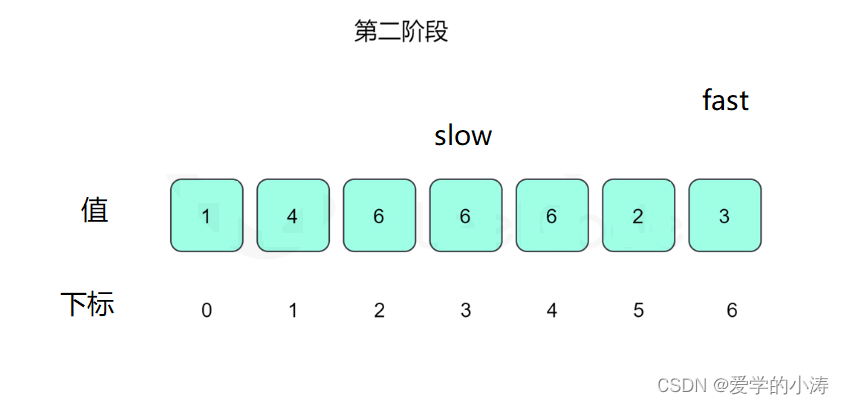
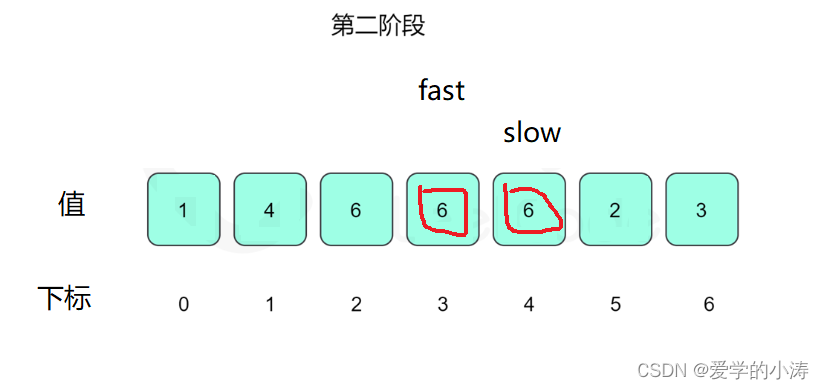
这时候slow=fast等于6 ，所以返回答案6

2.3、解题代码

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0, fast = 0;
        do{
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while(slow != fast);
        slow = 0;
        while(slow != fast){
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
}

​

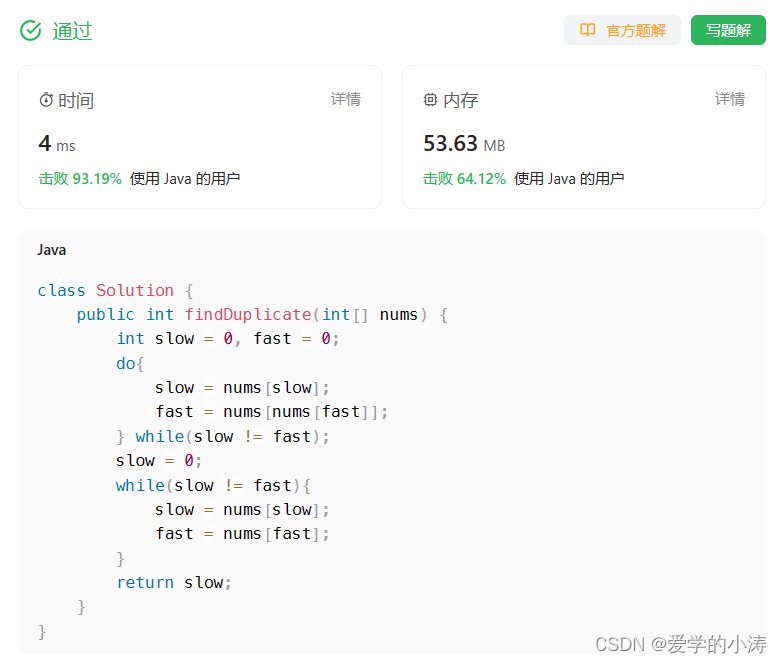
时间复杂度：O(n)O(n)O(n)。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。

空间复杂度：O(1)O(1)O(1)。我们只需要常数空间存放若干变量。

 【LeetCode力扣】相关：

【LeetCode力扣】11. 盛最多水的容器 （中等）-CSDN博客https://blog.csdn.net/m0_65277261/article/details/134102596?spm=1001.2014.3001.5502【LeetCode力扣】70. 爬楼梯 (简单)-CSDN博客https://blog.csdn.net/m0_65277261/article/details/134033485?spm=1001.2014.3001.5502【LeetCode力扣】86.分隔链表-CSDN博客https://blog.csdn.net/m0_65277261/article/details/133972240?spm=1001.2014.3001.5502

​