目录

1.结点总个数

1.1 局部静态变量法

思维

代码

不足之处

2.传指针法

程序代码

3.递归法

思想

程序代码

详细过程

2.叶子节点个数

思想

程序代码

3.第K层节点个数

思想

程序代码

4.二叉树深度

思想

程序代码

---

        求二叉树节点总个数、叶子节点个数、第k层节点个数、二叉树深度等等都是二叉树较为经典和常见的，下面详细介绍这些内容的实现方法及其思想、原理。

1.结点总个数

1.1 局部静态变量法

思维

        首先，最容易想到的计算总结点个数的方法，就是在遍历二叉树的时候，设置一个 变量，每一次访问到 非空节点，该变量的值就+1，遍历二叉树完后，该变量的值就是二叉树的节点总个数。

       但是，这个变量如何创建，创建什么样的变量 就成了问题，假如是在函数内部创建一个普通变量，如下，则会产生一个问题：每次遍历节点的时候，++ 的 size 是同一个 size吗？ 答案是否定的。

        如下图，当进入以节点 a 为参数的 LeafSize1 时，这里面创建的 size加一了；然后进入以 节点 b为参数的 LeafSize1，但是，以节点 a 为参数 和 以节点 b 为参数，是两个不同的函数栈帧，意为着其开辟的size 不是同一块内存中的，自然也就不是同一个 size（如右下角 栈区内存示意图，两个函数栈帧是两块不同的空间）。所以，这样子写的话，无论如何都无法计算节点总个数。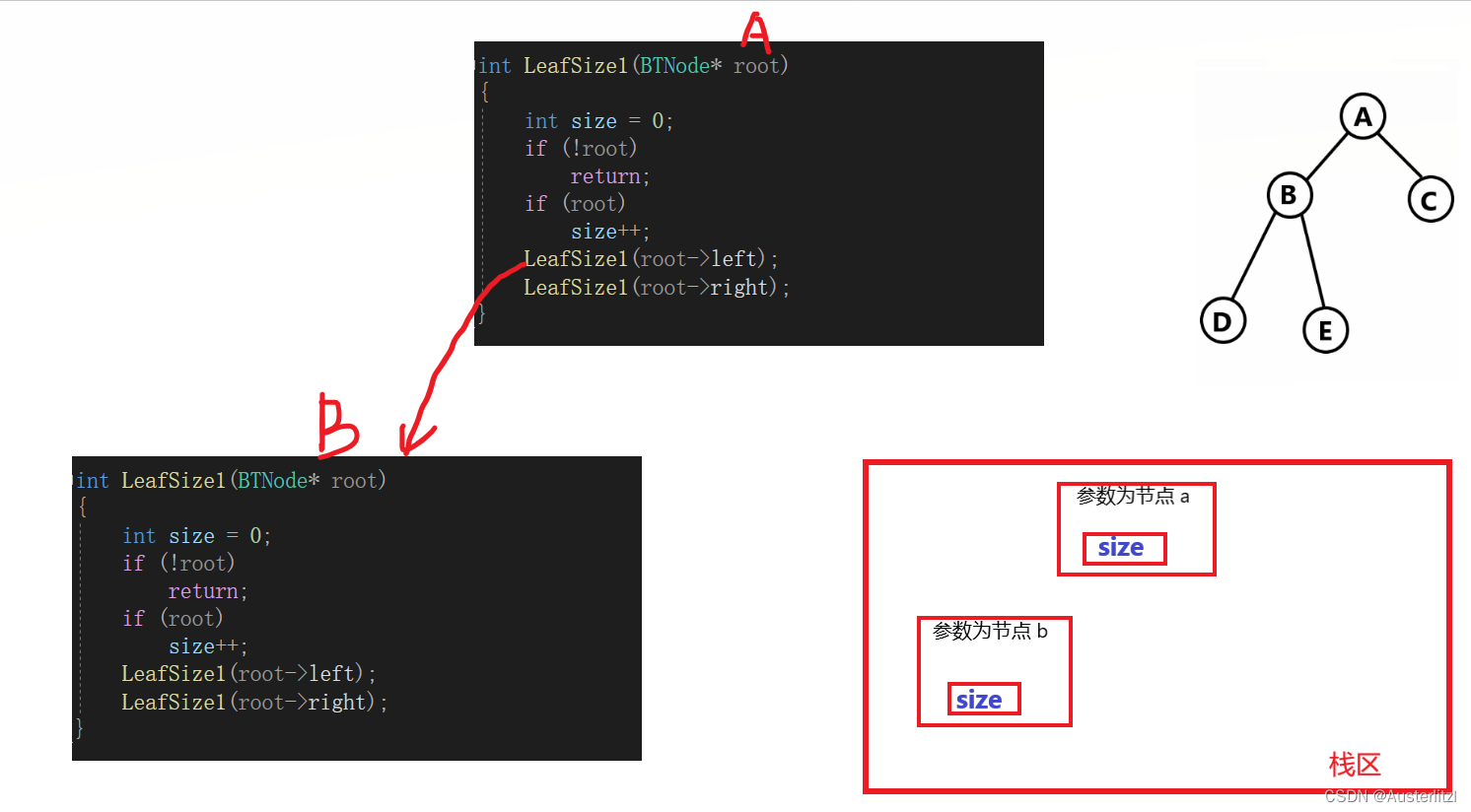

        那既然这是局部变量，每次创建新的函数栈帧都会重新创建该变量，此时将这个变量设置成全局变量不就可以了吗？这样创建的变量size，在静态区，每次创建的函数栈帧虽然都在栈区，但是一直使用的都是静态区的那一个size。如下，这样可以保证最后得到的结果是节点总个数。

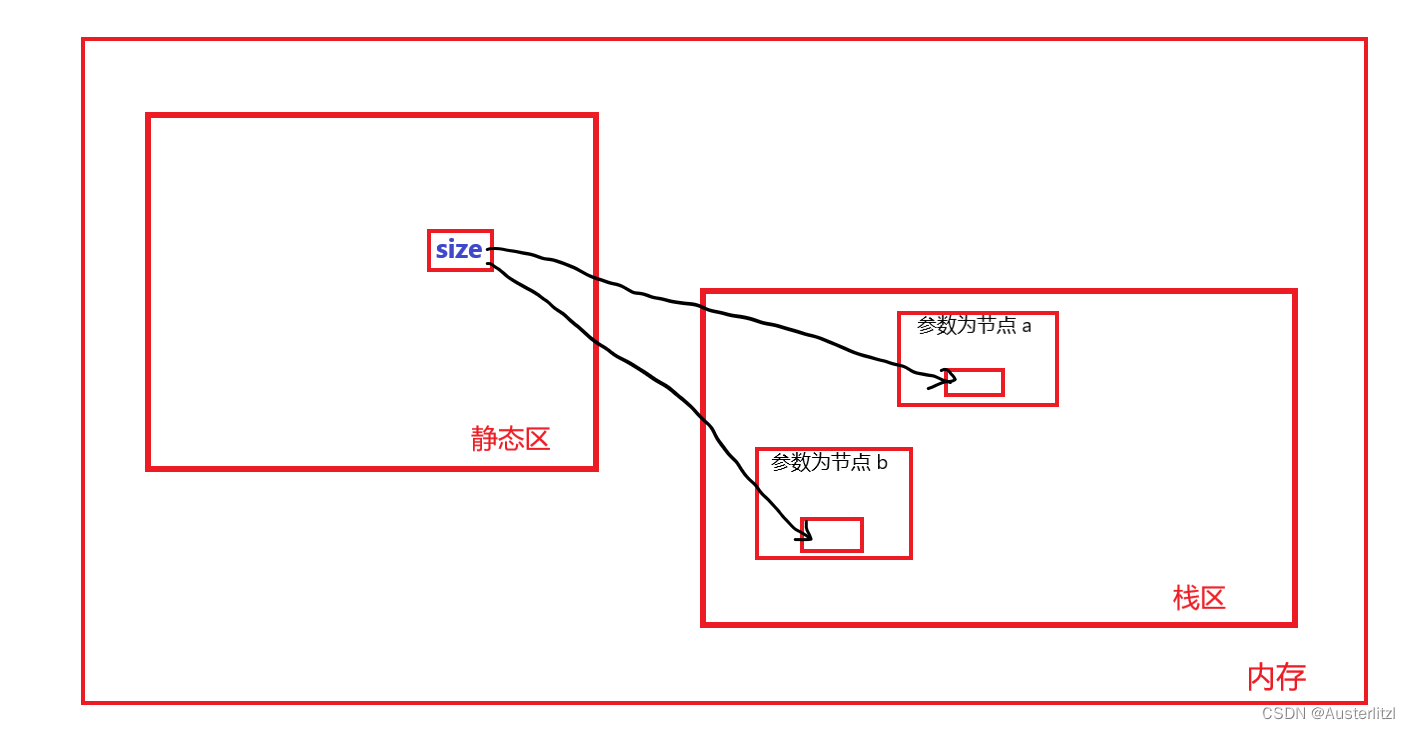
代码

        如下，在 size 前面加上 static ，将其设置成静态区的全局变量。每一次递归调用该函数，++的都是处于静态区的size。

int LeafSize1(BTNode* root)
{
	static int size = 0;//全局变量
	if (!root)
		return;
	if (root)
		size++;
	LeafSize1(root->left);
	LeafSize1(root->right);
    return size;
}

不足之处

        但是，这种方法也存在很大的不足。比如，只能计算一颗二叉树的节点总个数。如下运行结果：发现三次计算该二叉树节点总个数值都不同。

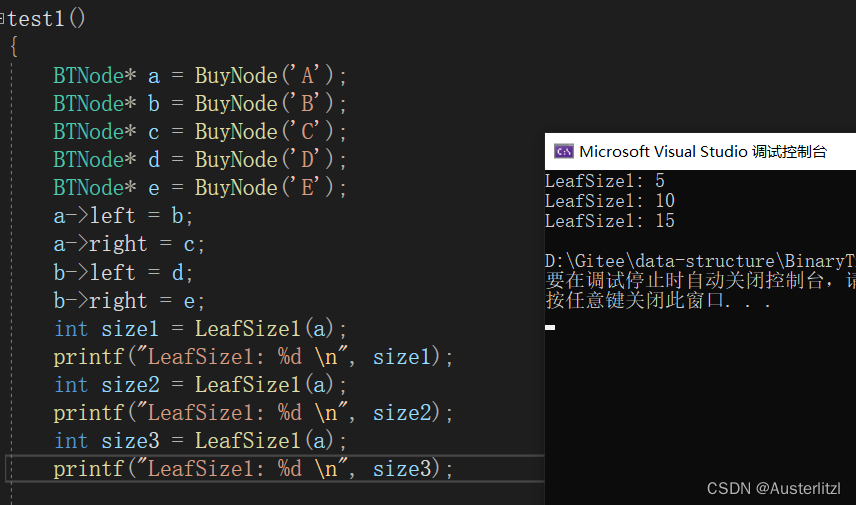
        这是因为，由于我们创建的是局部静态变量，所以，只能在最开始调用该函数的时候进行初始化。并且，由于是递归调用该函数，所以也无法判断递归到哪一层结束，也就没办法在本轮递归结束的时候，设置size 为0。

        具体过程如下两张图所示。size的值由于无法在每次计算节点总个数的时候初始化为0，同时也没有办法判断在每一次递归结束的时候置为0，也就只能无限制地增加下去。

第一次计算二叉树节点总个数：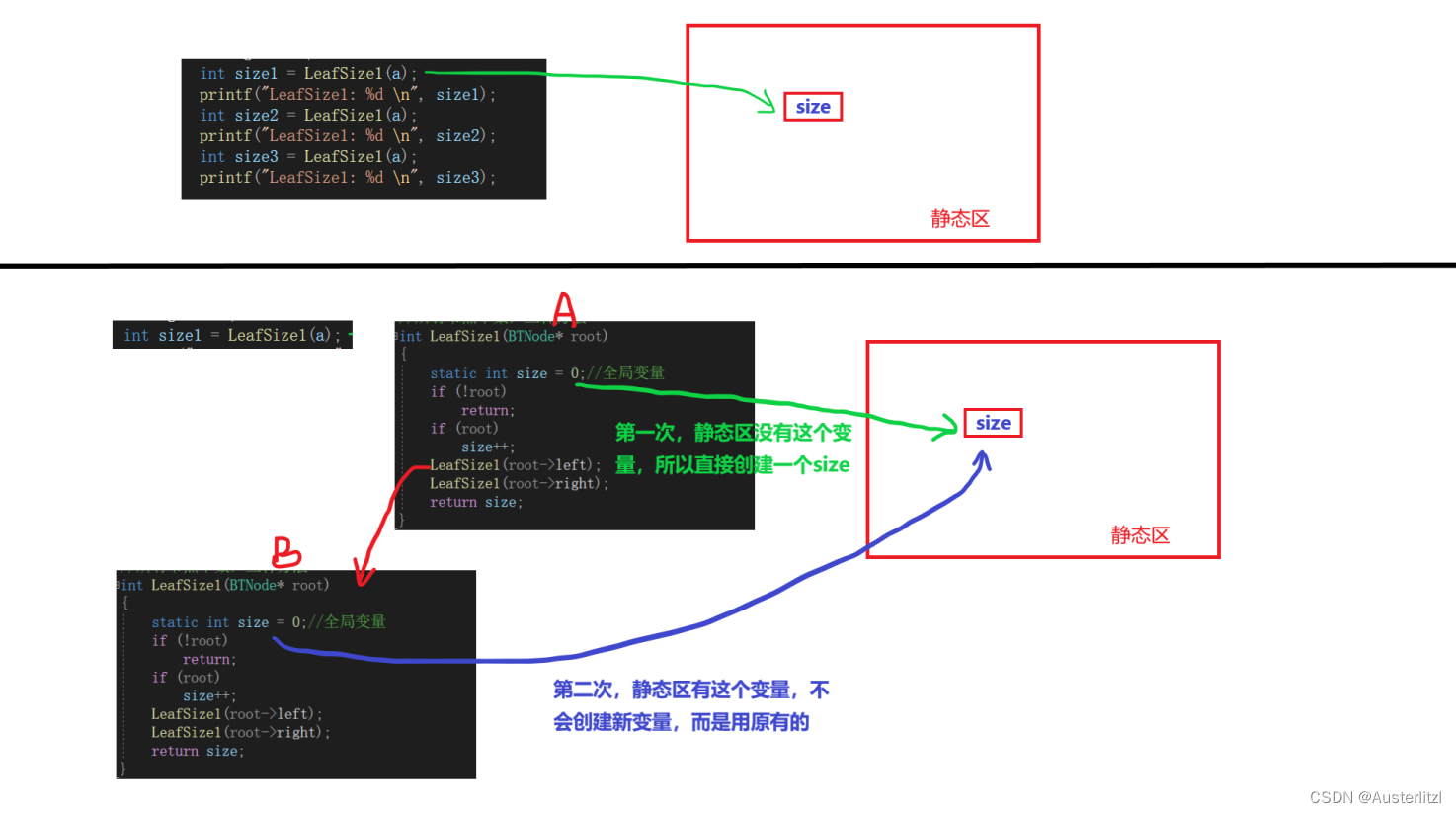

第二次计算二叉树节点总个数：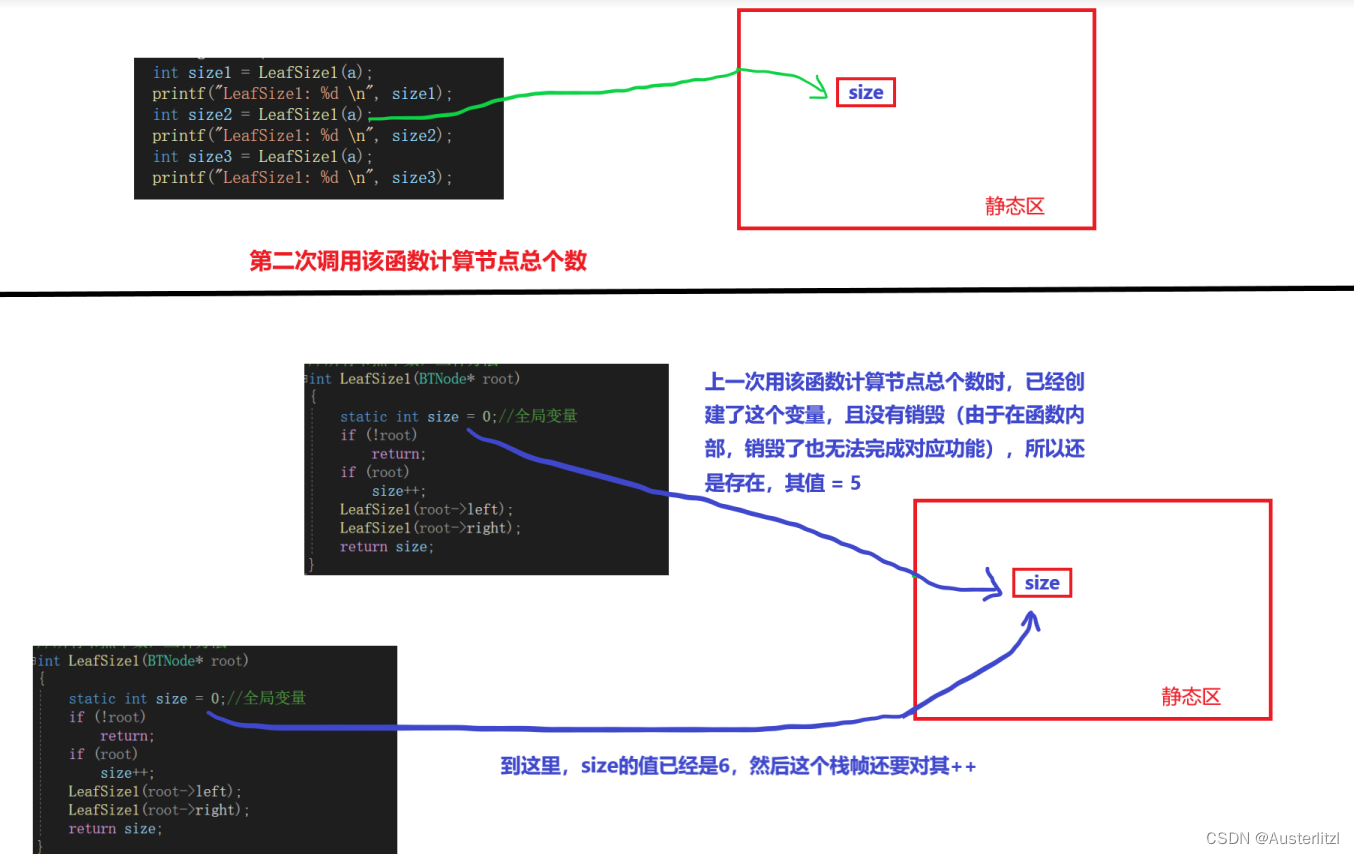

        所以，这显然不是一个好办法。

2.传指针法

        既然在函数内部设置变量无法达到想要的效果。那么我们可以尝试在函数外部设置对应的变量，然后每次调用该函数的时候，传入指针即可。示意图如下：

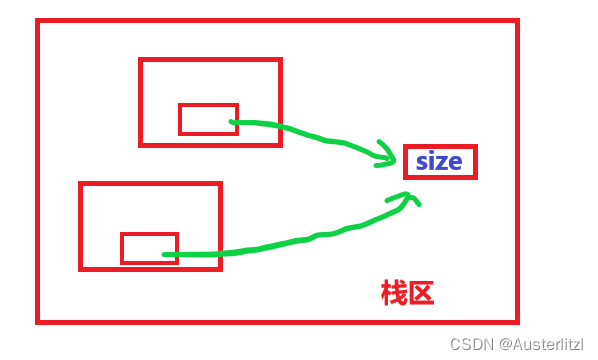
程序代码

         如下，不需要设置返回值，因为一直改变的就是传入的变量，直接在函数外部取即可。

void LeafSize2(BTNode* root, int* size)
{
	if (!root)
		return;
	if (root)
		(*size)++;
	LeafSize2(root->left, size);
	LeafSize2(root->right, size);
}

         运行结果也是如预期。无论是新建变量来计算，还是在下一次计算时将变量值设为0，都可以满足需求。

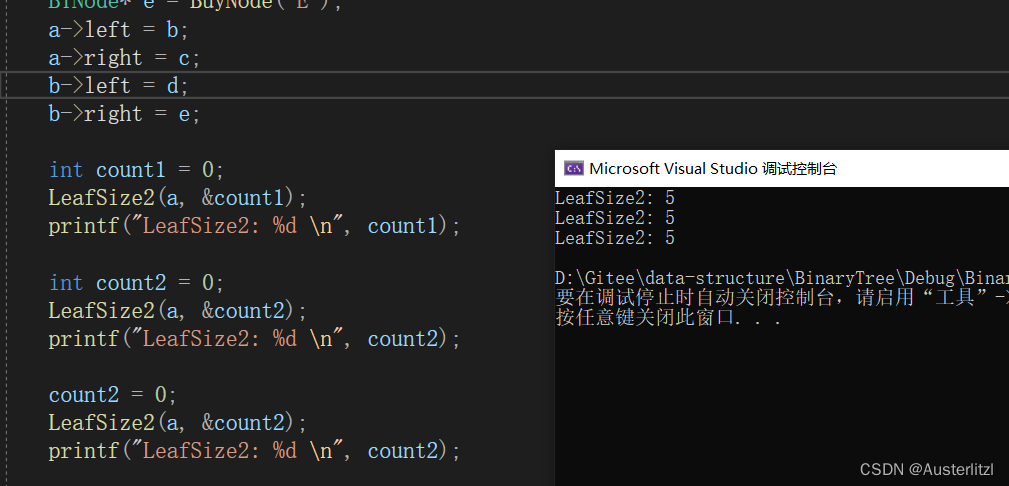
        因此，这种方法是比较推荐使用的。

3.递归法

 递归的两个基本要素：

    1、递归关系式：确定关系式，即原问题是如何分解为子问题的

    2、递归出口：确定递归到什么时候终止。

同时、一个递归函数我们是默认它能够完成所需功能的。

思想

        在这里，首先准备递归出口：当递归到传入指针为NULL时，自然就结束了，返回0，因为传入参数为 NULL的情况下，自然不是节点。

        递归关系式：先求左子树的节点个数，再求右子树的节点个数，最后加上根节点。

        所以，只需要判断当前参数是否为NULL，是NULL，表示当前没有节点，返回0，否则返回左子树的节点个数+右子树的节点个数+1。

程序代码

        代码如下。

int LeafSize3(BTNode* root)
{
	return root == NULL ? 0 : LeafSize3(root->left) + LeafSize3(root->right) + 1;
}

详细过程

        这里和递归遍历二叉树是非常类似的，如下，一开始以节点 a 为参数，然后进入函数直接判断，参数root 不为NULL，那么返回 LeafSize3(root->left) + LeafSize3(root->right) +1 ;  毫无疑问，这里要先调用 LeafSize(root->left) 。以节点a 的左孩子为参数调用函数，直到以节点d 为参数，其左右节点都是NULL，所以返回值都是0，如蓝色箭头和数字所示。

        同时，以节点d 为参数的这一块调用也结束，返回一个值，其值是孩子节点数之和再+1，由于其左右孩子都返回0，所以最后返回的结果是1。符合要求，因为d节点及其所有孩子节点一共也就它自己这一个。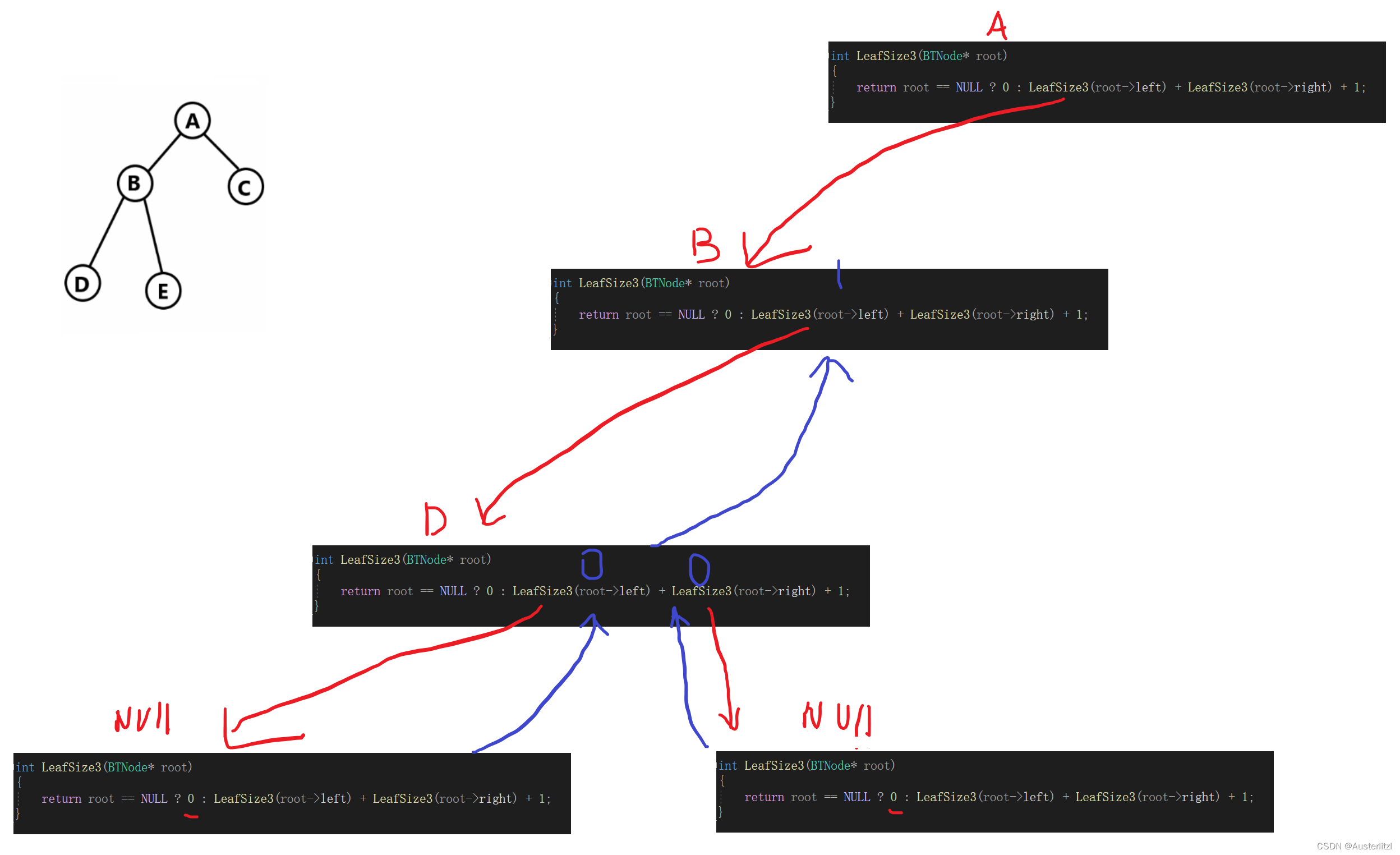

        上图过程完毕，返回到以 b节点为参数的函数栈帧中，如下过程，应该调用 LeafSize3(root->right); 由于root 是节点b，所以其右孩子理所当然是节点e。如下图，节点e左右孩子均为NULL，所以它调用的函数栈帧均返回0，再加上1，它返回的结果也是1。

        然后到了以 节点b 为参数的函数栈帧返回的时候了，其返回值是 1+1 +1，所以返回3，如下图蓝色标识。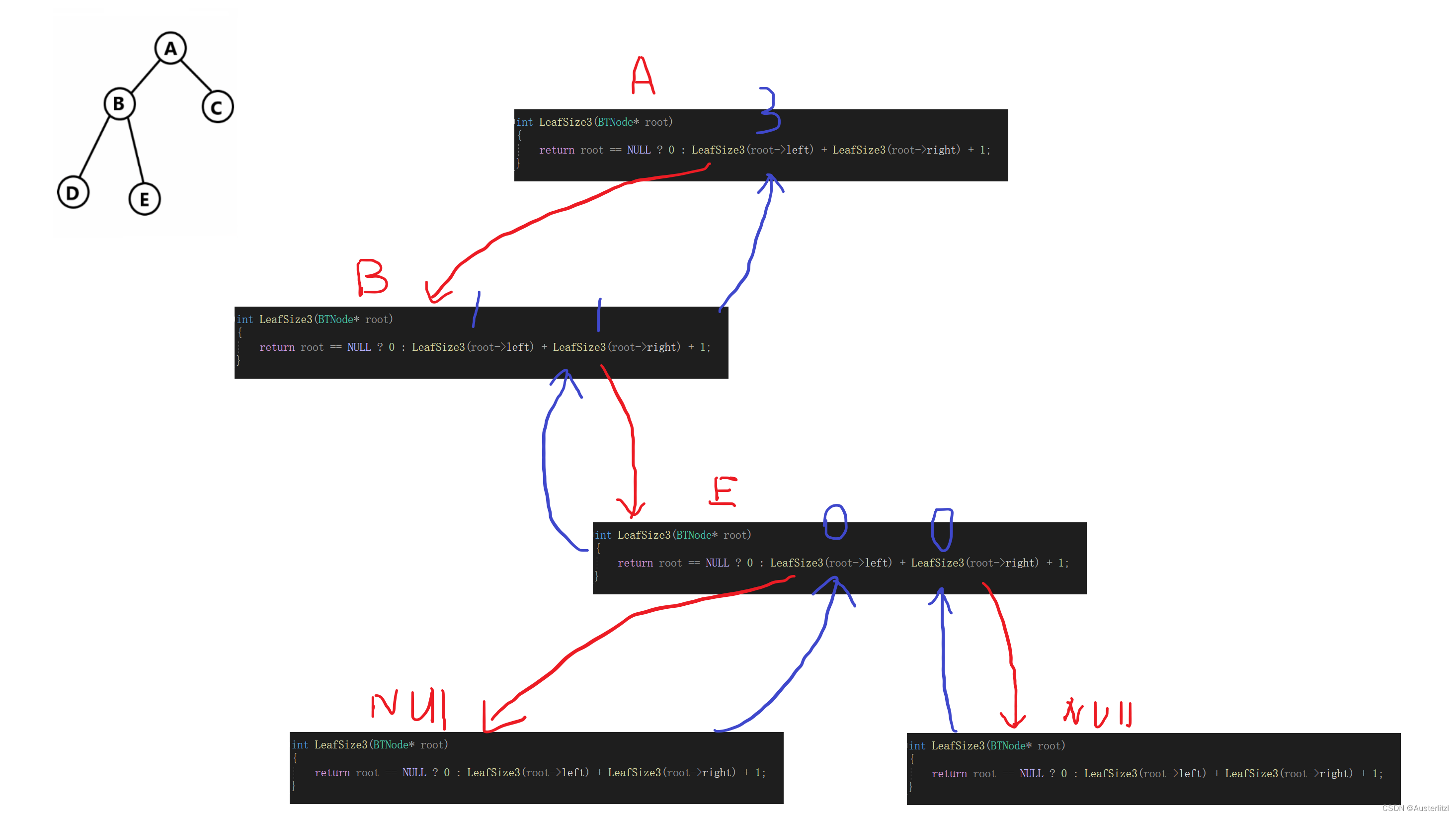

         然后又回到以节点a 为参数的函数栈帧中，应该调用 LeafSize3(root->right); 节点a 的右孩子无疑是节点c，由于其左右孩子都是NULL，故以节点c 为参数的函数栈帧返回值也是1。所以整个递归最后的返回值就是 3+1+1  等于5。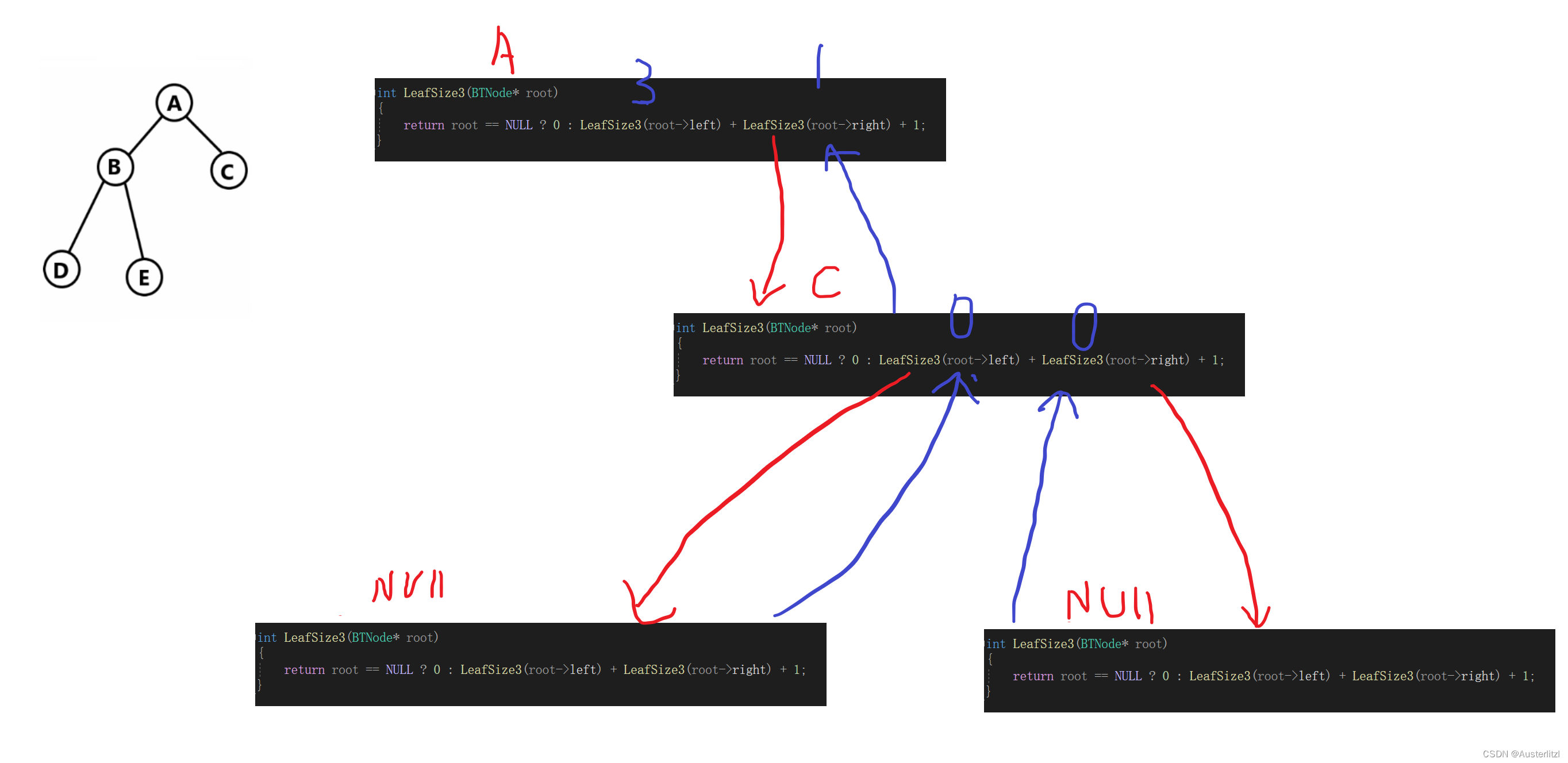

2.叶子节点个数

思想

        求叶子节点个数，当然也可以像上面一样有多种方法，只是把判断普通节点时的操作，换成判断为叶子节点的操作即可。这里简单地讲一讲用上面第三种方法——递归法来完成。

        首先，递归关系式就是：返回左右子树的叶子节点个数。

        而对于递归终止条件，不是简单地遇到叶子节点就返回1。如下图，如果只判断传入参数是否为叶子节点，遇到某个节点，只有一个孩子的时候，就与发生如下情况，会报错。所以，既要判断传入参数是否为叶子节点，也要判断是否为NULL。

程序代码

//叶子节点个数
int TreeLeafSize(BTNode* root)
{
	if (!root)
		return 0;
	if (root->left == NULL && root->right == NULL) //叶子返回1
		return 1;
	return    TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3.第K层节点个数

思想

        既然要求第k层，那么传入参数必然要多一个k，表示求该层节点个数。递归关系式很容易：返回左右子树第k-1层的节点个数（因为当前树的根节点算一层，所以递归下去每次减去一层）。

        和上一个一样，一方面，要判断是否到了第k层，到了第k层就直接返回1，这样子第k层之下的就不用再遍历了，免做无用功；另一方面，也是要判断传入参数是否为空，如果为空直接返回0。

        首先来看如何判断递归是否到达第K层，如下图（先不要看递归终止条件，看这个递归过程即可），每下一层，传入参数的 k 就减一。要求第3层的节点个数，实际上只要递归深入两层即可，所以，要求第k层节点个数，实际上只递归下去了k-1层，即，只要传入的参数 k 等于1，就到达了第K层。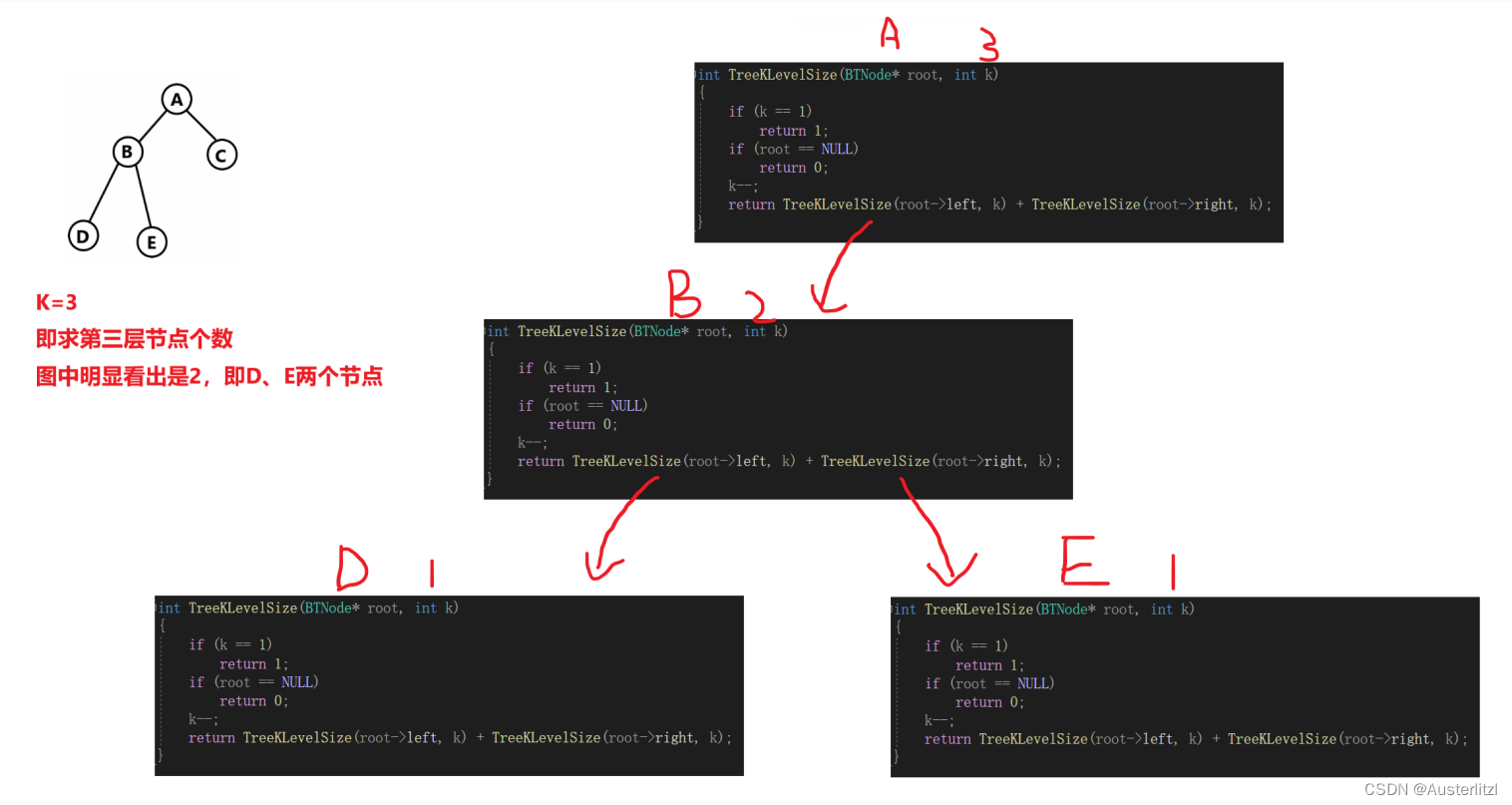

        但是，在这里是先判断是否到达第k层，还是先判断当前节点是否为空？我们假设，第k层如果为空，第k-1层不为空，我们可以到达第k-1层，然后进入第k层，此时如果先判断传入参数k，这时k=1，返回1，但是实际上第k层是没有节点的，就会造成错误。如下图蓝色数字，原本节点a的右子树应该返回的结果是0，但是由于到了第k层，先判断k==1，所以最后返回了2，是错误的：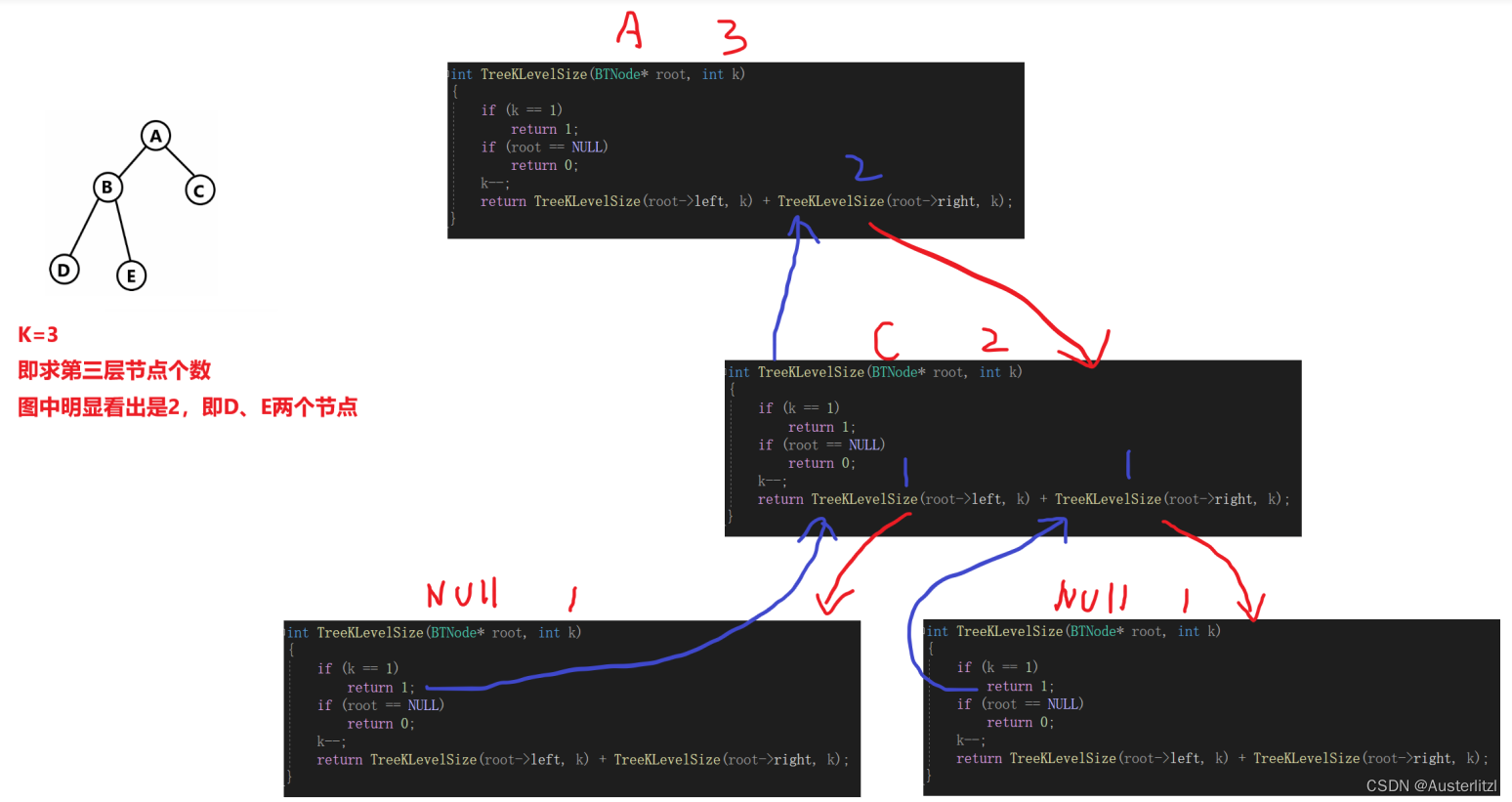

        所以如下面代码所示，要先判断当前节点是否为空。因为在这个算法的设计下，递归是无法递归到第k层之下的，所以大可放心。

程序代码

//第k层节点个数
int TreeKLevelSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	k--;
	return TreeKLevelSize(root->left, k) + TreeKLevelSize(root->right, k);
}

4.二叉树深度

思想

        依然使用递归法，这里的递归关系式就有小小的不同了：如果左子树的深度大于右子树，返回左子树深度+1，否则返回右子树深度+1（+1代表加上当前树的根节点所在层）。递归终止条件依然是遇到空节点返回0。

        但是，如下图的代码，虽然可行，效率却极其低下。可以自己尝试画一下递归展开图，就拿上面一直做例子的二叉树作为参考。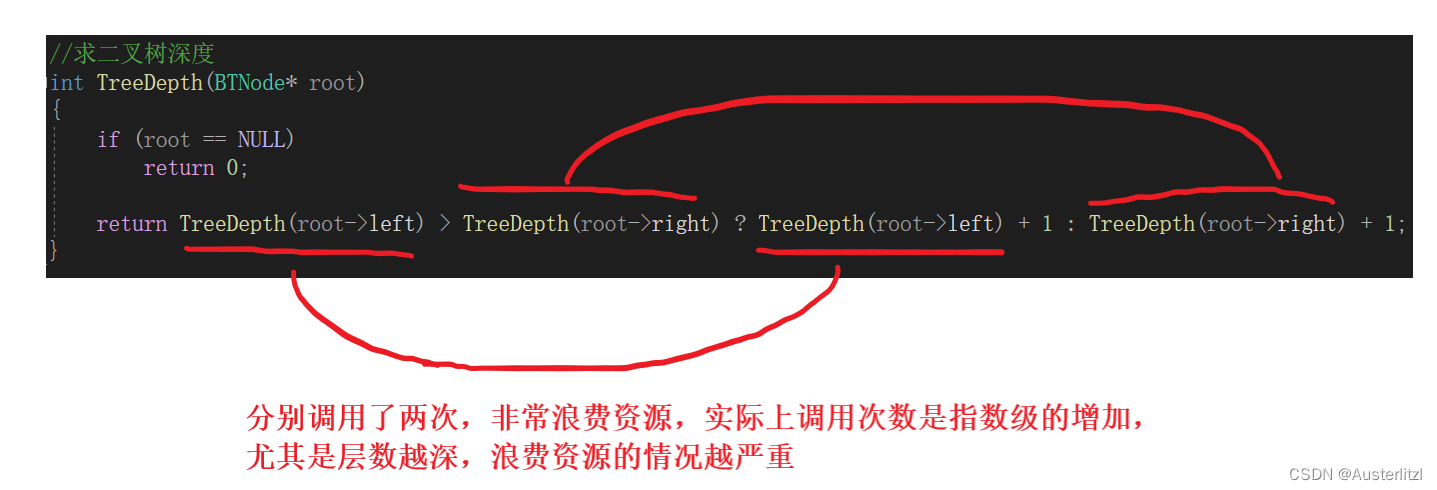

        所以，我们用两个变量 将左右子树的深度存起来，比较这两个变量大小即可。如下面的代码。

程序代码

//求二叉树深度
int TreeDepth(BTNode* root)
{
	if (root == NULL)
		return 0;
	int left = TreeDepth(root->left);
	int right = TreeDepth(root->right);
	return left > right ? left + 1 : right + 1;
}