---

作者：一个喜欢猫咪的的程序员

专栏：《数据结构》

喜欢的话：世间因为少年的挺身而出，而更加瑰丽。                                  ——《人民日报》

---

 

目录

时间复杂度：

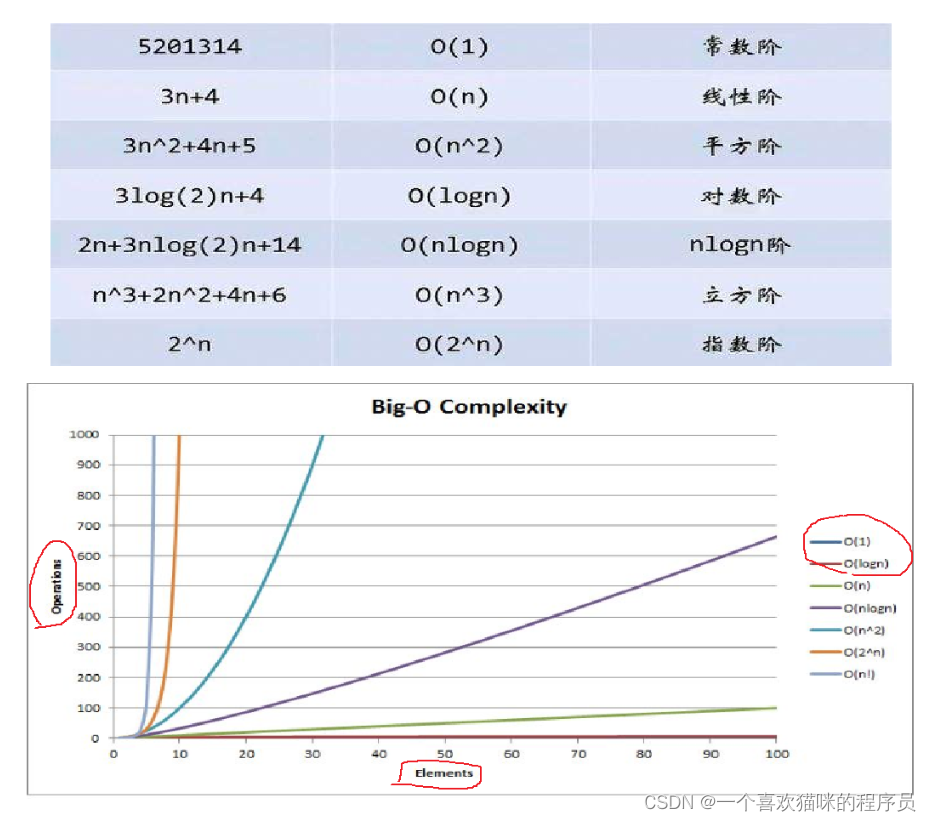
大O渐进表示法：

空间复杂度：

 常见复杂度对比：

---

 我们学数据结构之前我们已经写过了不少代码，我们在写代码的过程中，我们往往追求的是效率，那我们怎么来衡量一个代码的效率呢？

这就涉及到了本章的知识点：时间复杂度和空间复杂度！

因此衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

• 时间复杂度主要衡量一个算法的运行快慢，
• 空间复杂度主要衡量一个算法运行所需要的额外空间。

但我们一般比较在乎时间复杂度。

---

时间复杂度：

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

这里的函数指的是数学函数，而不是编程语言的函数。

执行的次数指的是循环的次数，以及递归时候函数调用的次数。

 我们先来看一个问题：下面这个代码执行了几次？

// 请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}

我们结合下图来理解一下：圆圈一和圆圈二都循环了N次，而圆圈3 循环了2N次，圆圈4循环了M次。一和二是嵌套关系，圆圈一每循环一次圆圈二循环N次，所以N次圆圈一应该是执行了N^2。圆圈3和4都是普通的循环，所以三个加起来为：N^2+2N+M，这是一个具体的时间复杂度。

 而我们平常算的时间复杂度是一个大概值，我们运用了一种计算方法：大O渐进表示法！！！

---

大O渐进表示法：

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

推导大O阶方法：

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

 我们观看这三个规则很抽象，我们下面通过一些例子来理解一下：

// 计算Func2的时间复杂度？
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}//O(2N+10)=O(N)

此代码我们容易算出它的具体的时间复杂度为2N+10。

我们这边利用了规则2和3，2N+10中2N为最高项，所以时间复杂度为2N，然后最高项2N存在，2这个常数去掉，所以最后是时间复杂度为O（N）。

// 计算Func4的时间复杂度？
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}//O(100)=O(1)

本题跟前几题不太一样，因为本题的时间复杂度的具体值是一个参数（100）。

我们利用规则1，O(100)就变为了O(1)。

当我们以后面试或者考研面试的时候，我们经常是不看代码，以思想来算他的时间复杂度，我们来试一下不看代码算出冒泡排序（N个数）的时间复杂度：

void BubbleSort(int* a, int N)

我们假设它N个数进行冒泡排序，第一个数执行了N次，第二数N-1个数，第三个数N-2个数.......以此类推。第N个数就执行一次。那时间复杂度O(N+N-1+N-2+.....+1)。

这里就涉及到了等差数列，等差数列求和如下：

Sn=[n*(a1+an)]/2

那这里我们时间复杂度就变为O(0.5N^2+0.5N)=O(N^2)

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
// [begin, end]：begin和end是左闭右闭区间，因此有=号
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}//O(logN)

 我们利用下图理解一下：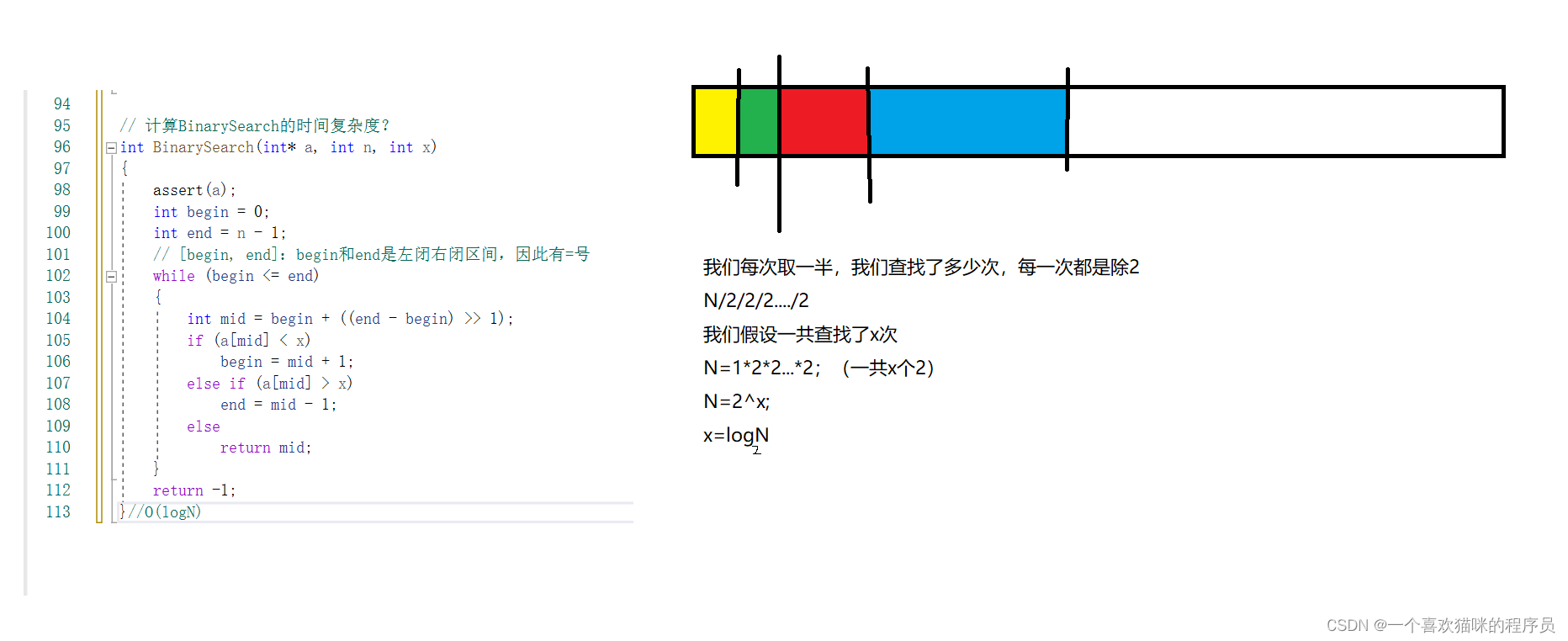

 我们在算数据结构的时间复杂度的时候。当遇到对数时，因为我们用键盘输入不了底数，所以我们经常把底数2省略，只写logN。但我们只省略2为底数的时候，当3（或者其他常数）为底数的时候，不省略。

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
if (1== N)
return 1;
return Fac(N - 1) * N;
}//O(N)

当我们在算递归的时候，时间复杂度的具体值我们可以理解为：一次递归算一次，这里一共N次所以一共N次。

我们将这个题目改一下再来算一下：

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
if (1== N)
return 1;
for (int i = 0; i < N; i++)
{
;
}
return Fac(N - 1) * N;
}//O(N^2)

这里我们要算一下它具体的时间复杂度：

当为N时，循环N次；当为N-1时，循环N-1次；.......；当为1时，执行1次；

累加后为：N+N-1+N-2+....+1+N(递归的次数)=0.5N^2+1.5N;

 我们理解了这些例子再发过来理解一下规则：

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

推导大O阶方法：

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

---

空间复杂度：

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

这里指的是是在函数内部临时开辟的空间的个数。

重复定义的话也算一个。

递归一次也算一个。

我们通过以下例子来看一下：（不再讲解已将答案写在每个代码最后）

// 计算Func4的空间复杂度？
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
}//O(1）

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}//O(N)

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}//O（N)

---

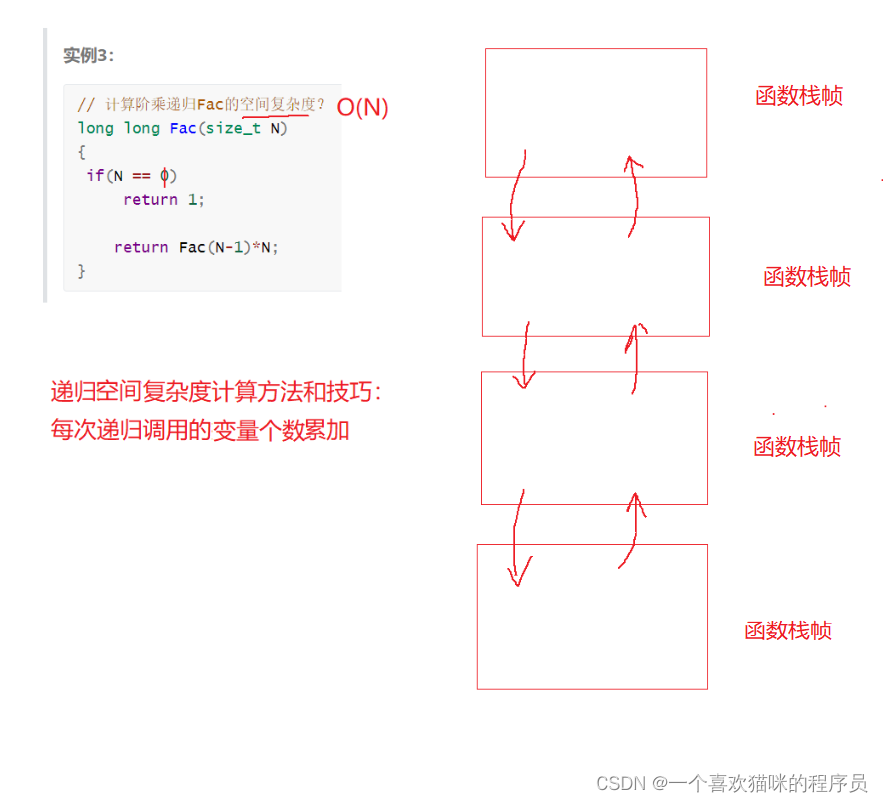
 常见复杂度对比：