一、前言

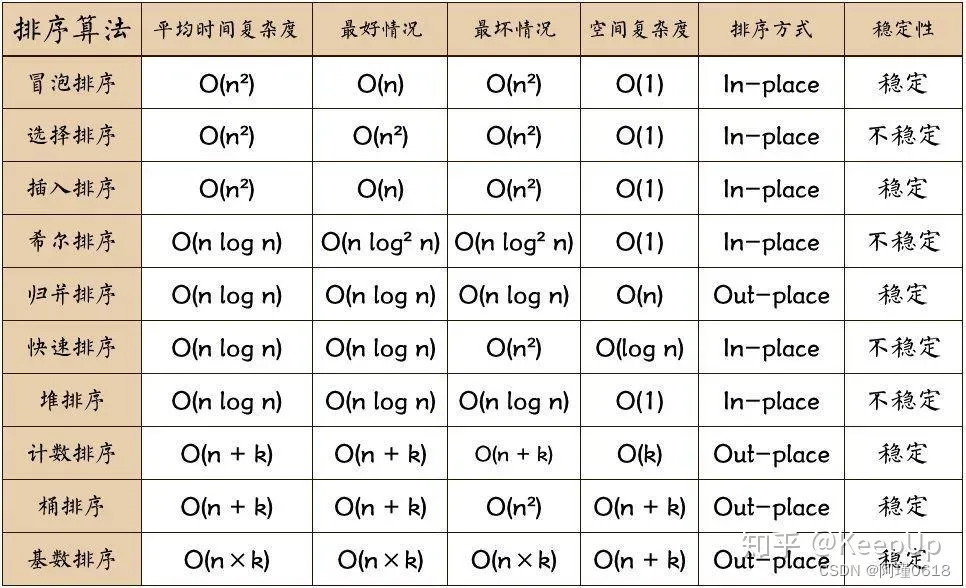
关于排序，有一些术语，例如算法的稳定/不稳定，内排序和外排序等，需要我们了解一下

稳定：当未排序时a在b前面且a=b，排序后a仍然在b前面

不稳定：当未排序时a在b前面且a=b，排序后a可能会出现在b后面

内排序：数据记录在内存中进行排序

外排序：由于数据太大，在排序过程中需要访问外存

---

二、冒泡排序

冒泡排序的效率十分低下，但是胜在排序过程形象易懂，适用于教学使用。

通过对数列的遍历并比较相邻的元素，将目标元素逐步移动到数组的尾端，就像泡泡慢慢冒出水面，因此得名。

2.1 算法描述

（1）从头到尾比较相邻元素，如果第一个大于第二个（升序）就将二者交换位置

（2）重复n-1遍第一步（最后一个元素一定是最小的所以不用排了）

2.2 动图展示

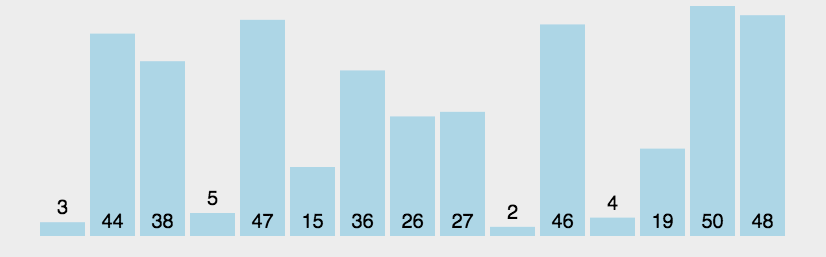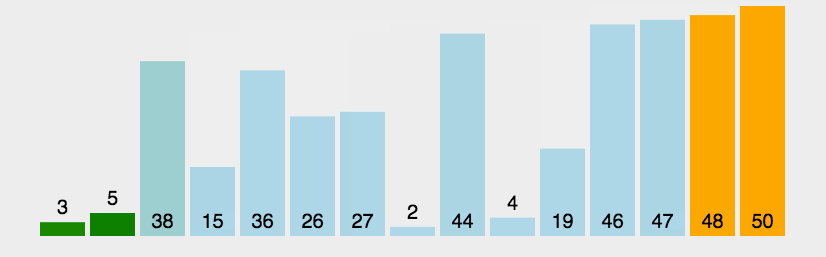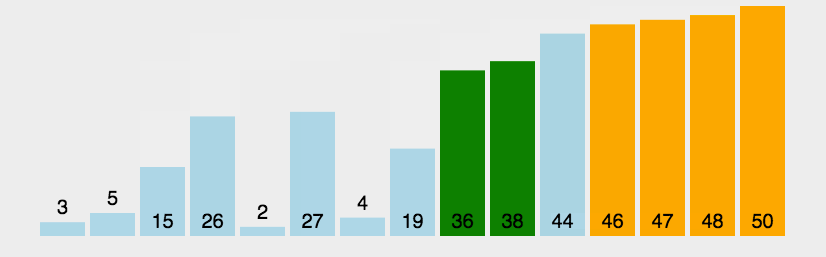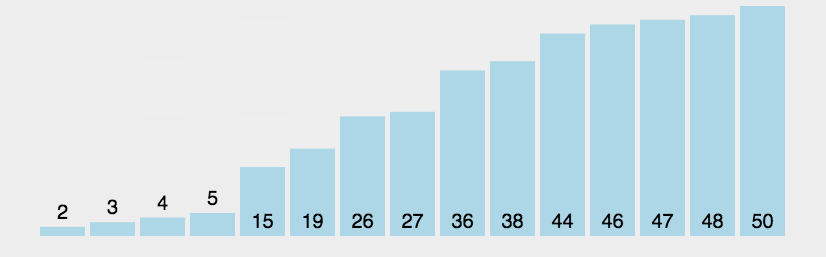
2.3 代码实现

void BubbleSort(int* a, int n) //冒泡排序
{
	for (int i = 0; i < n - 1; i++) //重复n-1次
	{
		for (int j = 1; j < n - i; j++) //单趟冒泡排序
		{
			if (a[j - 1] > a[j])
			{
				int tmp = a[j]; //交换元素
                a[j] = a[j - 1];
                a[j - 1] = tmp;
			}
		}
	}
}

2.4 算法优化

如果遍历一遍数组后没有发生任何元素交换，说明数组已经有序，排序就可以结束了。

优化后的代码如下：

void BubbleSort(int* a, int n) //冒泡排序
{
	for (int i = 0; i < n; i++)
	{
		bool flag = false; //flag每次循环重置为false
		for (int j = 1; j < n - i; j++)
		{
			if (a[j - 1] > a[j])
			{
				int tmp = a[j];
                a[j] = a[j - 1];
                a[j - 1] = tmp;
				flag = true; //如果发生元素交换，flag赋值为true
			}
		}
		if (flag == false) //如果单趟冒泡后flag没有发生改变说明已经有序
			break;
	}
}

---

三、选择排序

选择排序是表现最稳定的算法之一，但它的效率也很低下，无论情况的好与坏它的时间复杂度都是O(n2)。

3.1 算法描述

（1）遍历未排序的部分找出最小值（升序），将其与未排序部分的第一个元素交换

（2）重复n-1遍第一步（最后一个元素一定是最大的所以不用排了）

3.2 动图展示

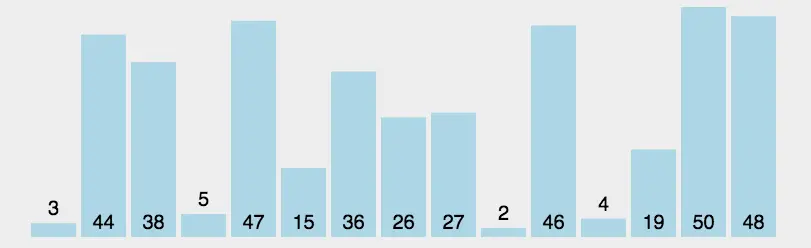
3.3 代码实现（优化版）

上面的动图中每次遍历只寻找最小值，我们可以优化一下，每次遍历同时寻找最大值和最小值。

void SelectSort(int* a, int n) //选择排序
{
	int begin = 0, end = n - 1;
	int tmp = 0;
	while (begin < end)
	{
		int min = begin;
		int max = begin;
		for (int i = begin; i <= end; i++) //遍历寻找最大和最小值
		{
			if (a[i] > a[max])
				max = i; //保存最大值的下标
			if (a[i] < a[min])
				min = i; //保存最小值的下标
		}
		tmp = a[begin]; //将最小值交换到前面
		a[begin] = a[min];
		a[min] = tmp;
		if (max == begin) 
		{
            //最大值如果恰好在begin处，通过交换就到了min的位置，需要更新下标
			max = min;
		}
		tmp = a[end]; //将最大值交换到后面
		a[end] = a[max];
		a[max] = tmp;
		begin++; //更新头部位置
		end--; //更新尾部位置
	}
}

---

四、插入排序

插入排序的逻辑十分简单，将待排序的元素一个个插入到一个已经排好序的有序数列中，直到整个数列都有序为止。

过年的时候我们打扑克牌，将一堆无序的牌变得有序的过程实际上就是运用了插入排序的思想。

4.1 算法描述

（1）只有一个元素时默认有序，所以我们跳过第一个元素

（2）取出下一个元素，在已经排好序的序列中从后向前扫描并与取出的元素对比

（3）如果扫描到的元素大于取出的元素（升序），就将扫描的元素向后移一位

（4）重复步骤3，直到扫描到的元素小于或等于取出的元素，将取出的元素放入有序数列

（5）重复步骤2~5

4.2 动图展示

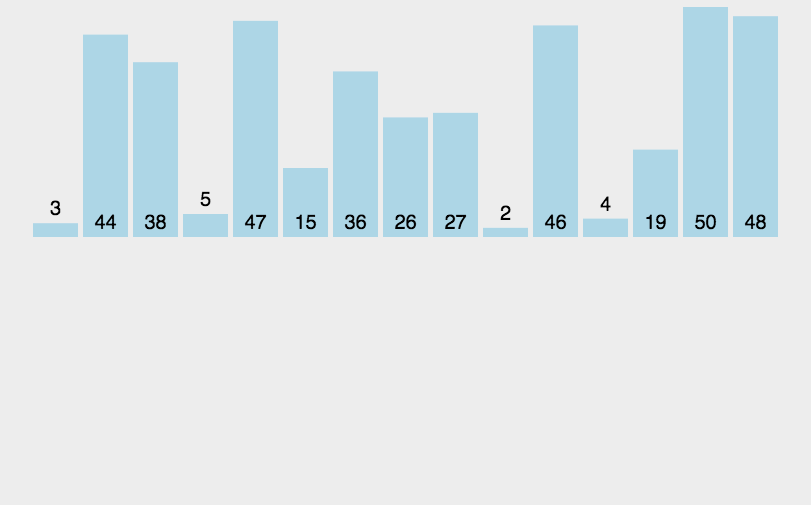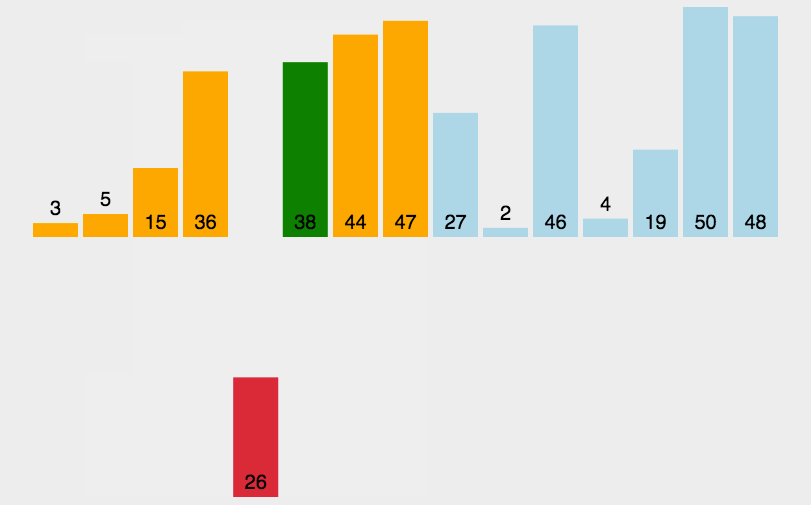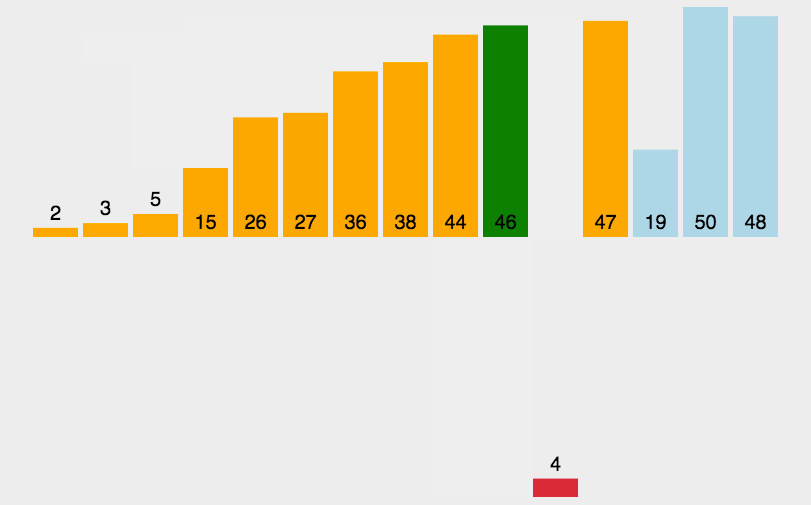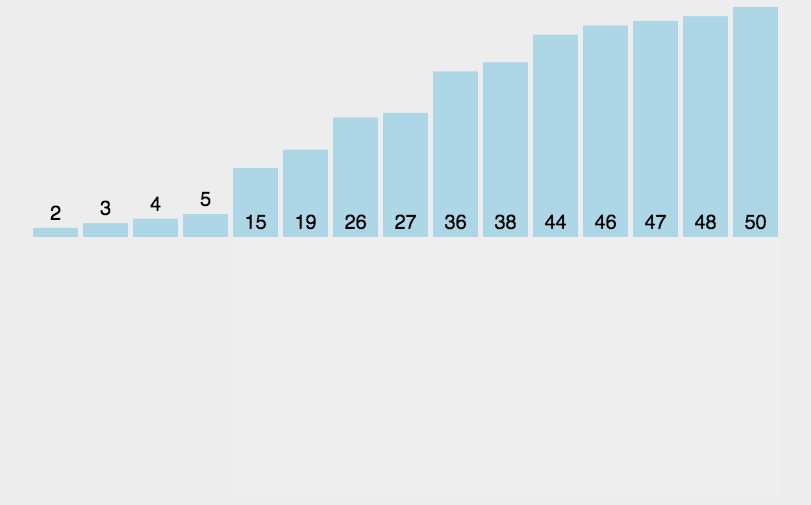
4.3 代码实现

void InsertSort(int* a, int n) //插入排序
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1; //有序序列的尾部位置
		int tmp = a[i]; //取出待排序元素
		while (end >= 0) //扫描有序序列
		{
			if (tmp < a[end]) //扫描到的元素大于取出的元素
			{
				a[end + 1] = a[end]; //将其向后移一位
				end--; //从后向前扫描
			}
			else //找到合适的位置
			{
				break;
			}
		}
		a[end + 1] = tmp; //将取出的元素插入
	}
}

---

五、希尔排序

希尔排序又称缩小增量排序，它也是插入排序的一种，由希尔（Donald Shell）于1959年提出，也是时间复杂度冲破O(n2)的第一批算法之一。

5.1 算法描述

（1）设定一个gap，并按照gap将待排序数列分割成若干子序列，对子序列分别进行插入排序

（2）将gap缩小，重复步骤1，当gap=1时就是插入排序

5.2 动图展示

5.3 代码实现

void ShellSort(int* a, int n) //希尔排序
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
					break;
			}
			a[end + gap] = tmp;
		}
	}
}

希尔排序是对插入排序的优化，当gap>1时都是预排序，目的是让数组不断趋近有序；当gap为1时数组已经很接近有序了，所以排起来就会很快。

---

六、堆排序

堆排序（Heapsort）是指利用堆积树（堆）这种数据结构所设计的一种排序算法，是选择排序的一种，通过堆来进行选择数据。

在前面学习数据结构堆的时候我们已经见过堆排序了，这里不再赘述。

6.1 算法描述

（1）先建堆，升序建大堆，降序建小堆

（2）将堆顶元素与堆尾元素互换，并排除出堆

（3）此时堆的性质被打破，通过向下调整算法调整为新的堆，重复操作2直至序列有序

6.2 动图展示

6.3 代码实现

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* arr;
	int size;
	int capacity;
}Heap;
void AdjustDown(int* a, int n, int root) //向下调整算法
{
	int child = root * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child = child + 1;
		}
		if (a[child] > a[root])
		{
			HPDataType tmp = a[child];
			a[child] = a[root];
			a[root] = tmp;
			root = child;
			child = root * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n) //堆排序
{
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i); //通过向下调整算法建堆
	}
	while (n > 1)
	{
		int tmp = a[0]; //将堆顶元素交换到堆尾
        a[0] = a[n - 1];
        a[n - 1] = tmp;
		n--; //排除原堆顶元素
		AdjustDown(a, n, 0); //调整被打乱的堆
	}
}

---

七、快速排序

快速排序是本文的重头戏，它是对冒泡排序的一种改进算法，在当前所有的内部排序算法中，快速排序被认为是最好的排序算法之一。

7.1 算法描述

（1）任选待排序序列中的某元素作为基准值，按照该值通过单趟排序将待排序的序列分为左右两个子序列，左子序列中的元素均小于基准值，右子序列中的元素均大于基准值（升序）

（2）分别对左右两个子序列重复步骤1，直至序列有序

7.2 单趟排序的实现

不同版本的快排核心思想都是一样的，区别在于单趟排序的方式不同 

7.2.1 hoare版本

大体思路

（1）选定待排序序列头部（或尾部）的元素作为key值，保存下标

（2）扫描待排序序列，一个从左到右寻找比key大的值，另一个从右向左寻找比key小的值，找到后将二者交换。

（3）当待排序序列扫描结束后，将序列头部的key与left位置处的元素交换，并返回left（此时left是key值的下标）

动图展示

代码实现 

int PartSort(int* a, int left, int right) //单趟排序hoare版本
{
    //left从待排序序列头部向后走，right从待排序序列尾部向前走
	int key = left; //将待排序序列的第一个元素作为key值
	while (left < right) //left小于right说明单趟排序没结束
	{
		while (left < right && a[right] >= a[key]) //right位置的值不比key小时向前走
		{
			right--;
		}
		while (left < right && a[left] <= a[key]) //left位置的值不比key大时向后走
		{
			left++;
		}
		tmp = a[left]; //此时right位置的值比key小，left位置的值比key大
		a[left] = a[right]; //二者交换
		a[right] = tmp;
	}
	tmp = a[key]; //把序列头部作为key值的元素交换到left位置，完成单趟排序
	a[key] = a[left];
	a[left] = tmp;
	return left; //返回left位置存放的key值
}

7.2.2 挖坑法

大体思路

（1）将待排序序列头部的元素存放到一个临时变量中作为key值，将key值原先的位置作为坑位

（2）从右往左寻找比key小的值，找到后将其填入坑中，并且其原来的位置成为新的坑

（3）从左往右寻找比key大的值，找到后将其填入坑中，并且其原来的位置成为新的坑

（4）重复步骤2~3直到待排序序列扫描完毕

（5）最后将key值填入坑中，返回key值下标

动图展示

代码实现 

int PartSort(int* a, int left, int right) //单趟排序挖坑法
{
	int tmp = a[left];
	int hole = left;
	while (left < right)
	{
		while (left < right && a[right] >= tmp)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= tmp)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = tmp;
	return left;
}

7.2.3 前后指针法

大体思路

（1）prev指针指向待排序序列开头，cur指针指向prev的下一个位置，将序列头部元素作为key值

（2）cur向后走寻找比key小的值，如果找到则prev++，并交换元素

（3）重复步骤2直到cur走到结尾，将key值与prev位置的值交换并返回key值此时的下标

动图展示

代码实现

int PartSort(int* a, int left, int right) //单趟排序前后指针法
{
	int midi = GetMidIndex(a, left, right);
	Swap(&a[left], &a[midi]);
	int key = left;
	int prev = left;
	int cur = left + 1;
	while (cur < right + 1)
	{
		if (a[cur] < a[key])
		{
			prev++;
			tmp = a[cur];
		    a[cur] = a[prev];
		    a[prev] = tmp;
		}
		cur++;
	}
	tmp = a[key];
	a[key] = a[prev];
	a[prev] = tmp;
	return prev;
}

7.3 递归实现快排

快排是一种二叉树结构的交换排序算法，因此我们可以用递归实现。

用递归实现快排比较简单，这里直接放代码 

void QuickSort(int* a, int left, int right) //递归实现快排
{
	if (left >= right)
		return;
	int key = PartSort(a, left, right);
	QuickSort(a, left, key - 1);
	QuickSort(a, key + 1, right);
}

7.4 非递归实现快排

非递归的方式需要用到栈，通过对待排序区间下标的压栈和出栈来实现快排

大体思路

（1）首先将待排序序列尾部的下标压入栈中，再将头部的下标压入栈中（因为后面出栈要先取出头部再取出尾部，栈的特性是后进先出）

（2）取两次栈顶元素，分别取出序列头部和尾部的下标，对这一区间进行单趟排序后获取key值的下标

（3）当key值不与原区间头部或尾部相邻时，以key值为分界将先前的区间拆分成两部分，分别压入栈中

（4）重复步骤2~3直到栈为空

代码实现

void QuickSortNonR(int* a, int left, int right) //非递归实现快排
{
	Stack st;
	StackInit(&st);
	StackPush(&st, right);
	StackPush(&st, left);
	while (!StackEmpty(&st))
	{
		int begin = StackTop(&st);
		StackPop(&st);
		int end = StackTop(&st);
		StackPop(&st);
		int keyi = PartSort2(a, begin, end);
		if (keyi + 1 < end)
		{
			StackPush(&st, end);
			StackPush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			StackPush(&st, keyi - 1);
			StackPush(&st, begin);
		}
	}
}

具体关于栈的实现可以前往 数据结构——栈-CSDN博客 查看

7.5 算法优化

（1）三数取中法

快速排序虽然效率高，但是还是有缺陷的。

当快排在排序大量有序或者接近有序的序列时，选择的key容易恰好为最小值，效率比较低下，会进行一些不必要的递归。

当递归调用层数过深，会导致栈溢出的情况，这里我们可以使用三数取中的办法来对这种情况进行优化。

三数取中，就是对比待排序序列头部的值、中部的值和尾部的值，选出三者中既不是最大也不是最小的值作为key值，并放到序列头部

其代码实现如下：

int GetMidIndex(int* a, int left, int right)//三数取中
{
	int mid = (left + right) / 2;
	if (a[left] > a[mid])
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] > a[right])
			return right;
		else
			return left;
	}
	else
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[left] < a[right])
			return right;
		else
			return left;
	}
}

具体的使用，我们只需要在单趟排序代码的开头加上这么一段就行：

int midi = GetMidIndex(a, left, right);
tmp = a[left];
a[left] = a[midi];
a[midi] = tmp;

 （2）小区间优化

快排在排序一个数据量为100万的无序序列时只需要递归20层，但排序一个8个数据的无序序列时就要递归3层。

在递归出的二叉树结构中，最底部的三层的递归次数竟然占用了全部递归次数的87.5%！

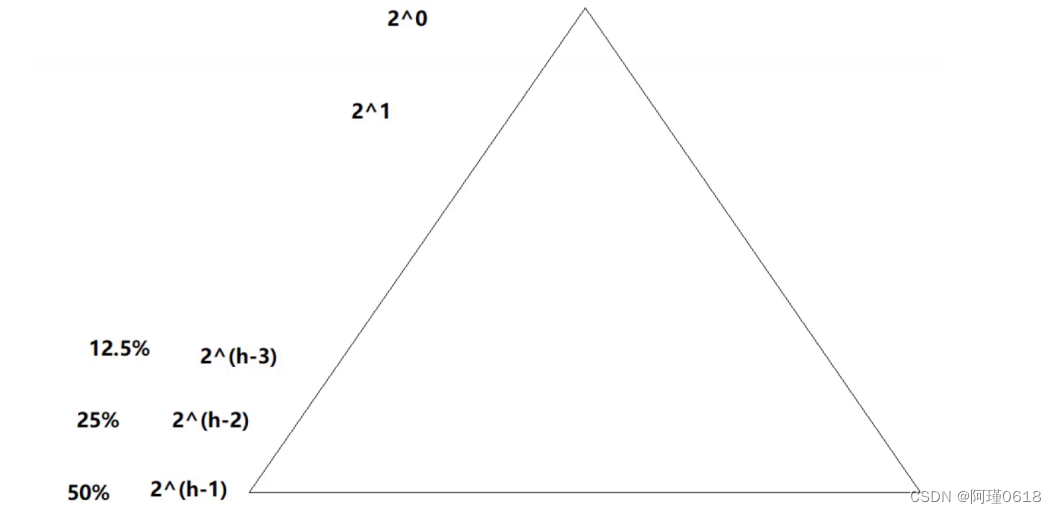
因此我们可以对递归实现快排的代码进行优化，当区间的数据量较小时，转为使用其他的排序算法

本质上是为了减少递归调用次数来提高效率

这里我们可以使用插入排序来排序数据量较小的区间

void QuickSort(int* a, int left, int right) //小区间优化版快排
{
	if (left >= right)
		return;
	if (right - left + 1 < 10)
	{
		InsertSort(a + left, right - left + 1);
		return;
	}
	int key = PartSort2(a, left, right);
	QuickSort(a, left, key - 1);
	QuickSort(a, key + 1, right);
}

小区间优化的思想对递归实现归并排序也tong'yang'sh 

（3）三路划分

虽然三数取中法能解决待排序序列有序或接近有序的情况，但是如果序列中有大量的元素和key相等，甚至整个序列所有元素都相等时，三数取中也无法解决这种情况

这时需要使用三路划分的思想

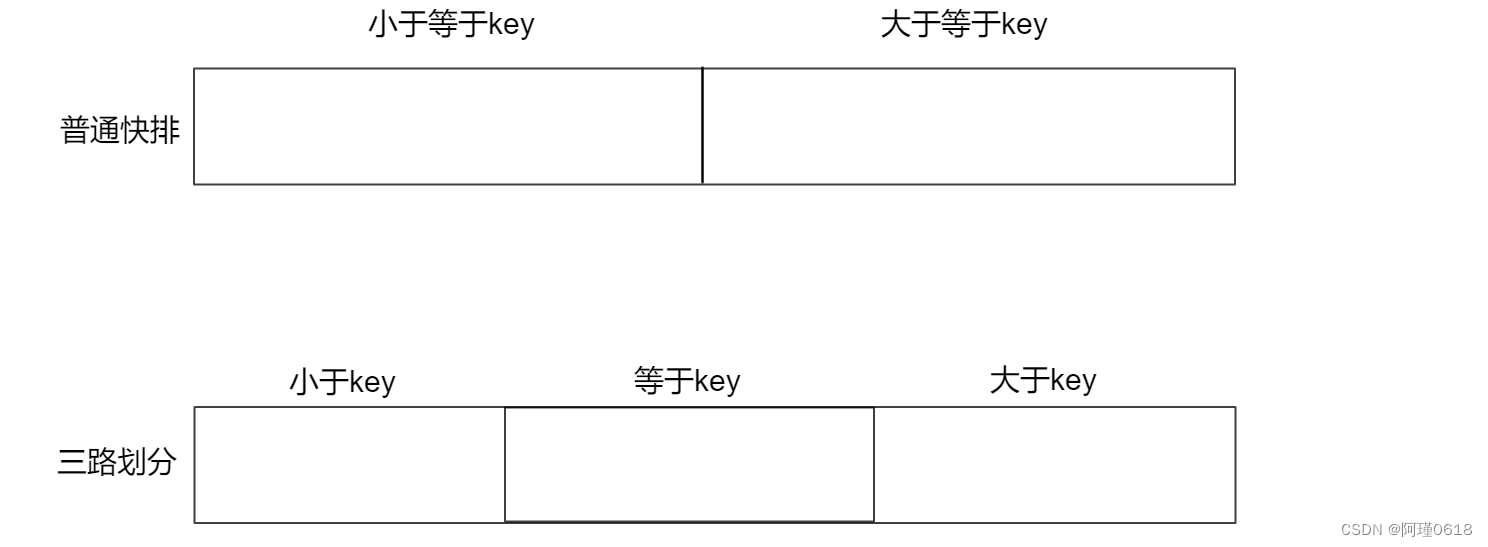
三路划分的大体思路：

（1）begin指向区间头部，cur指向begin的下一个位置，end指向区间尾部，以头部元素作为key

（2） 如果cur处的值小于key，则将begin和cur处的元素交换，二者各向后一步   

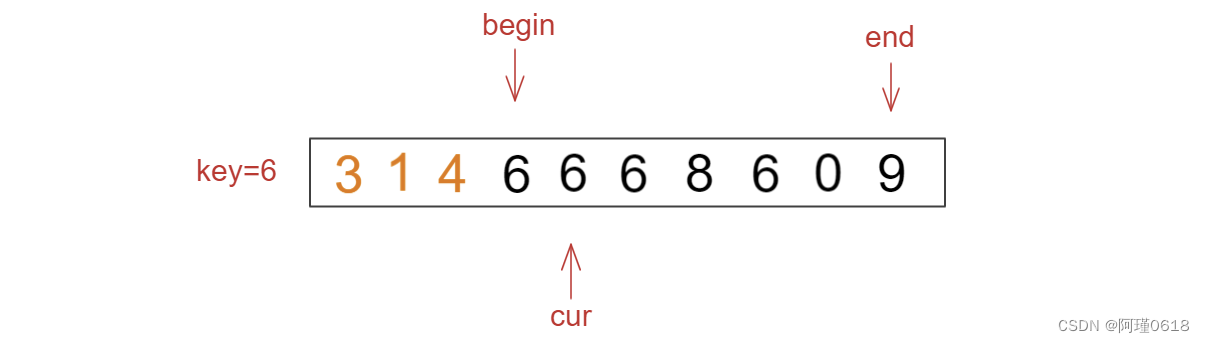
（3）如果cur处的值等于key，则cur向后走一步

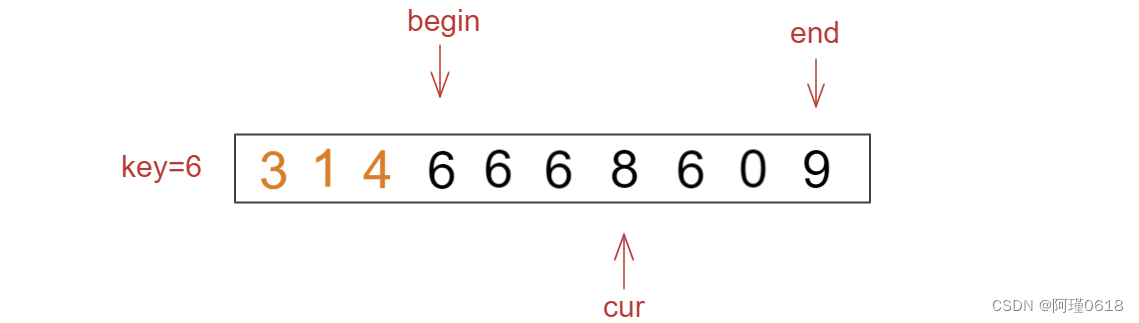
（4）如果cur处的值大于key，则将cur和end处的元素交换，cur向前走一步

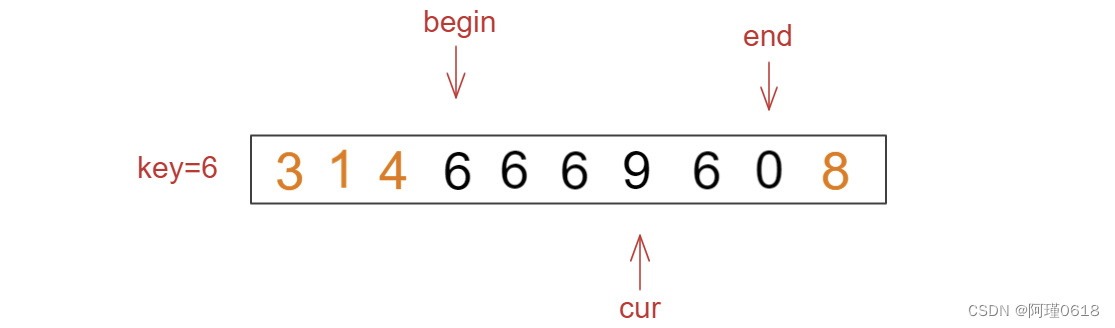
（5）重复以上步骤直到cur > end时结束

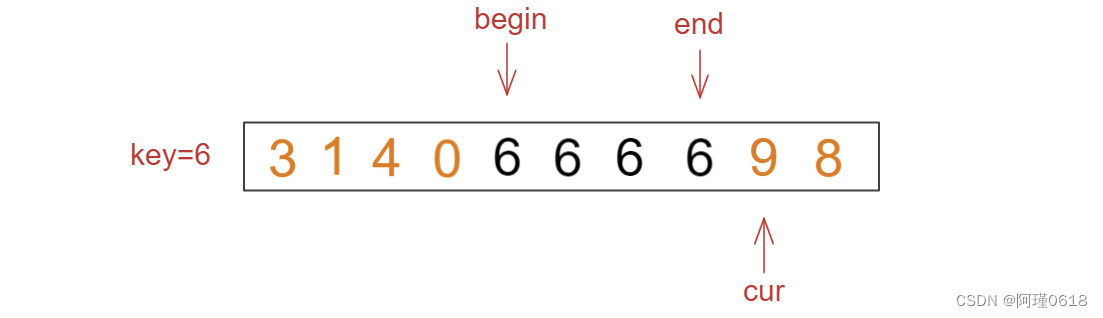
（6）对左边小于key的部分和右边大于key的部分进行递归

三路划分的代码实现：

void QuickSortThreeWay(int* a, int left, int right)//三路划分版快排
{
	if (left >= right)
		return;
	int begin = left;
	int end = right;
	int cur = begin + 1;
	int key = a[left];
	while (cur <= end)
	{
		if (a[cur] < key)
		{
			Swap(&a[cur], &a[begin]);
			cur++;
			begin++;
		}
		else if (a[cur] > key)
		{
			Swap(&a[cur], &a[end]);
			end--;
		}
		else
		{
			cur++;
		}
	}
	QuickSort(a, left, begin - 1);
	QuickSort(a, end + 1, right);
}

---

八、归并排序

归并排序的核心思想：分治

分治就是将一个复杂的问题分解成子问题，子问题再分解成更小子问题，直到最后子问题可以简单求解。在求二叉树的节点个数和二叉树的高度时我们也使用过这个思想。

将待排序的序列分解为两个子序列，再将子序列继续分解，直到每个子序列中只有一个元素，此时默认有序。再将有序的子序列逐渐归并到一起。

若将两个有序子序列合并成一个序列，称为二路归并。归并排序的逻辑图如下：

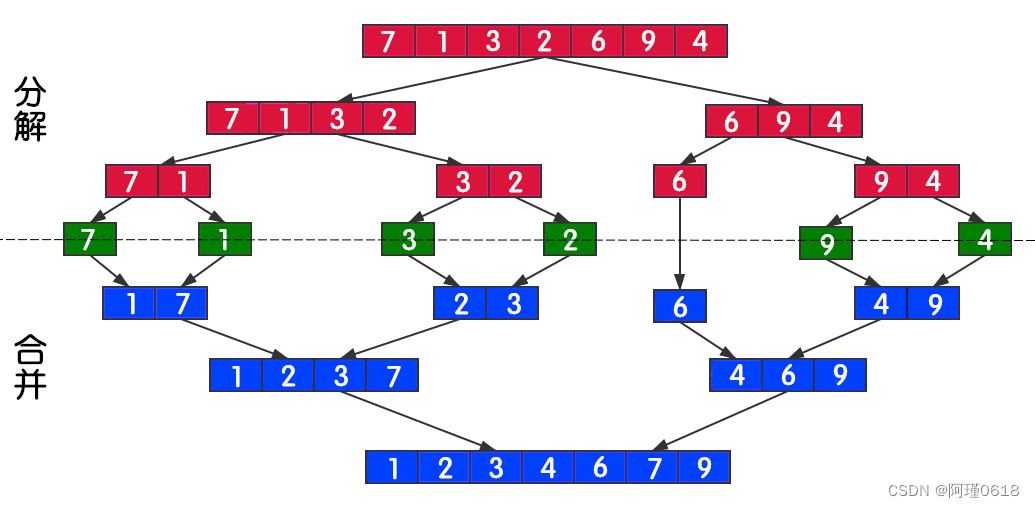
8.1 算法描述

（1）malloc一块和待排序序列大小相同的空间，用来临时存放归并后的序列

（2）通过递归或迭代将待排序序列拆分多个子序列

（3）子序列间两两归并到开辟出的空间中，具体操作可以参考两个有序数组合并

（4）将归并后的子序列用memcpy覆盖到原序列中

（5）重复上述操作直到序列有序

8.2 动图展示

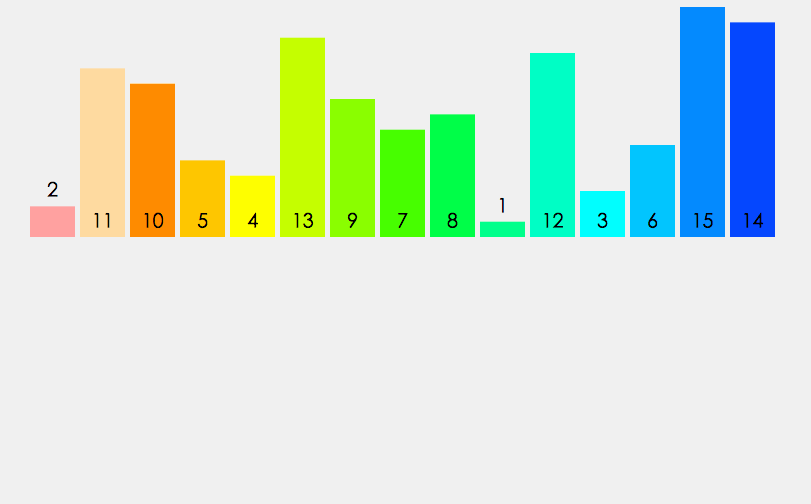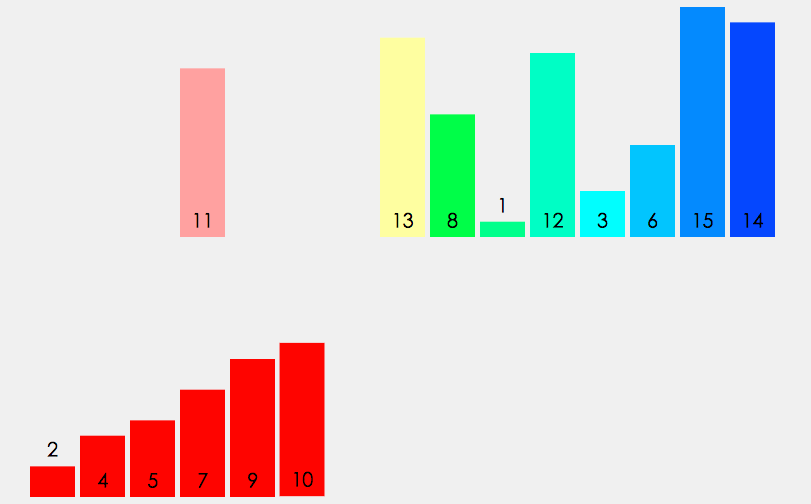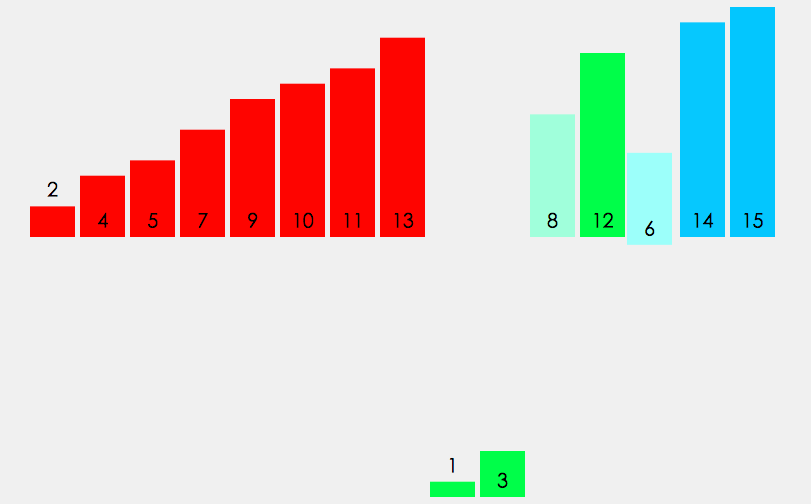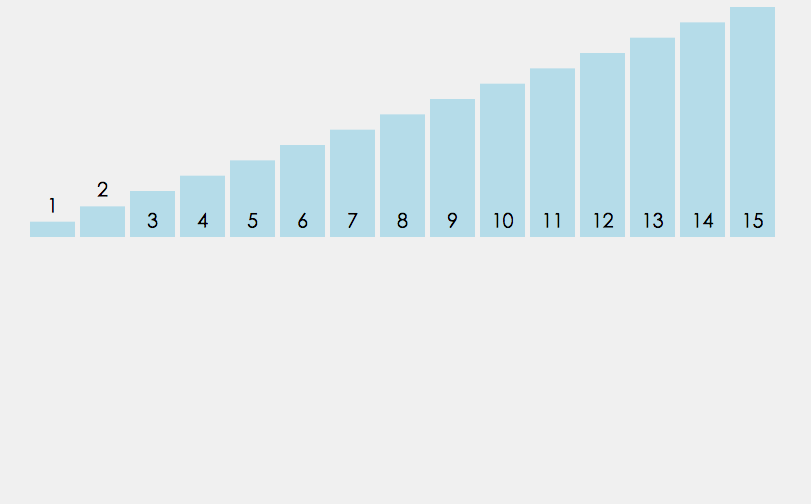
8.3 递归实现归并排序

大体思路

（1）通过递归将待排序序列不断的对半分，直到分出的子序列中只有一个元素

（2）计算出相邻两个子序列区间的边界，对二者进行归并

代码实现

我们不能每次递归都开辟一次空间，所以需要将主要的代码都放在子函数中，对子函数进行递归

//递归实现归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin == end)
		return;
	int midi = (begin + end) / 2;
	_MergeSort(a, begin, midi, tmp);
	_MergeSort(a, midi + 1, end, tmp);
	int begin1 = begin, end1 = midi;
	int begin2 = midi + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = malloc(sizeof(int) * n);
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

8.4 非递归实现归并排序

通过非递归来实现归并排序，最难解决的是边界问题

大体思路

（1）设定一个初始值为1的gap

（2）通过gap来分割子序列。每次分割出两个相邻的子序列进行归并，归并好一组就将其覆盖到原序列中

（3）重复步骤2直到第一轮归并结束

（4）gap乘2，重复步骤2~3，直到gap超过原序列的大小

对于边界问题，在分割子序列的时候可能会出现以下问题：

①两个子序列都越界

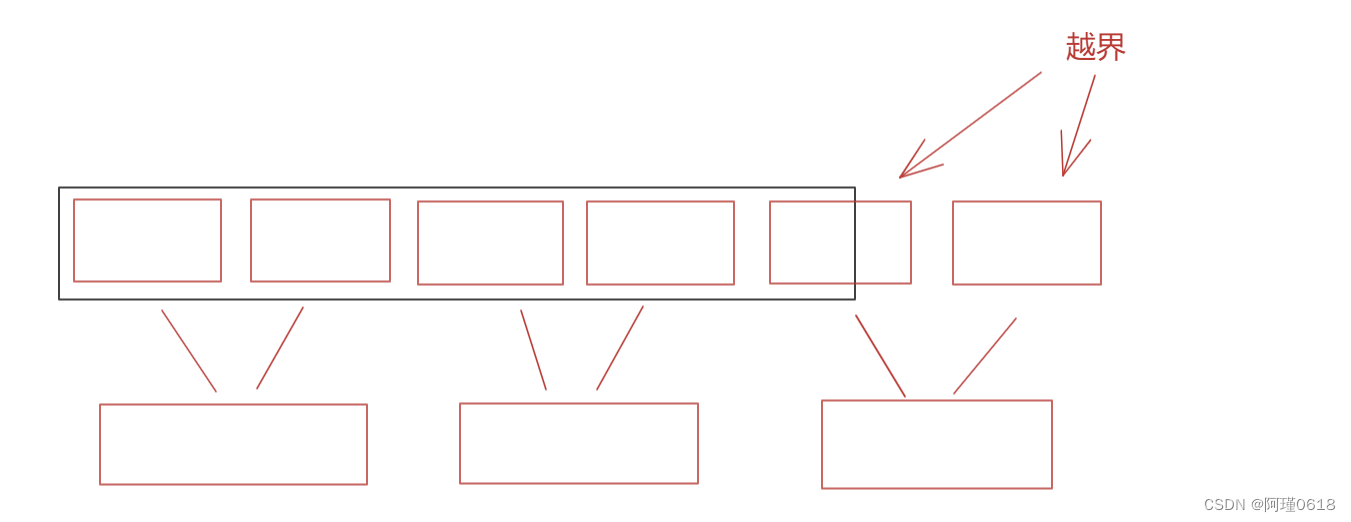
②只有第二个子序列越界 

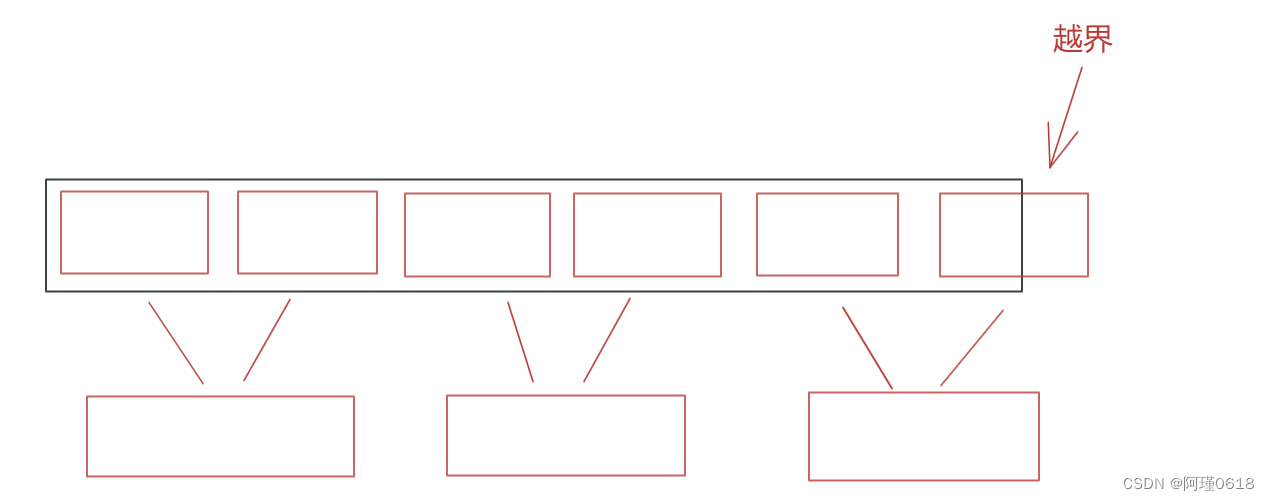
当相邻的两个子序列都越界时，我们就不对它们进行归并了，放在原序列中就好

当只有第二个子序列越界时，我们对越界的序列右侧进行修正即可 

代码实现

//非递归实现归并排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int j = i;
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}
		gap *= 2;
	}
	free(tmp);
}

九、计数排序

计数排序是一个不基于比较的排序算法，又被称为鸽巢原理，是对哈希直接定址法的变形应用。

其优势在于对一定范围内较集中的序列排序时，其时间复杂度低于任何一个基于比较的算法。

其劣势在于是一种用空间换时间的算法，依赖数据范围，只适用于范围较集中的整型数组。

9.1 算法描述

核心思想：统计待排序序列中每种元素出现的次数，按照顺序和出现的次数依次放入原序列中 

（1）首先遍历待排序序列找出最大值和最小值，算出序列元素的范围大小

（2）按照算出的范围开辟一块空间，用来存放统计出的元素个数

因为序列中元素的范围不一定从0开始，如果使用绝对映射（以元素的真实数值作为下标）就会浪费大量空间。当我们找出最大值和最小值后，将元素减去最小值就是它的相对位置

（3）遍历待排序序列，对每种元素出现的次数进行统计

（4）根据统计的结果，按照顺序放入原序列

9.2 动图展示

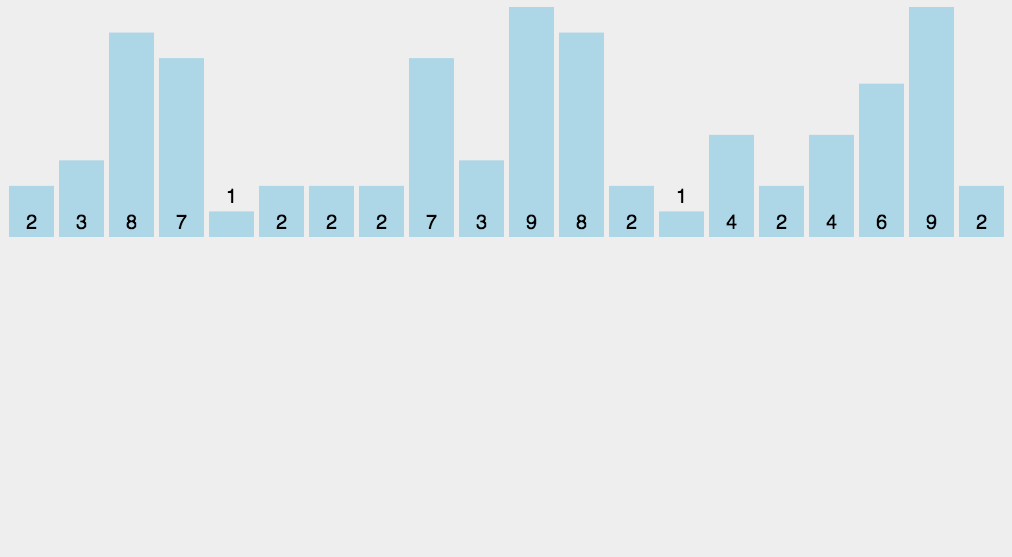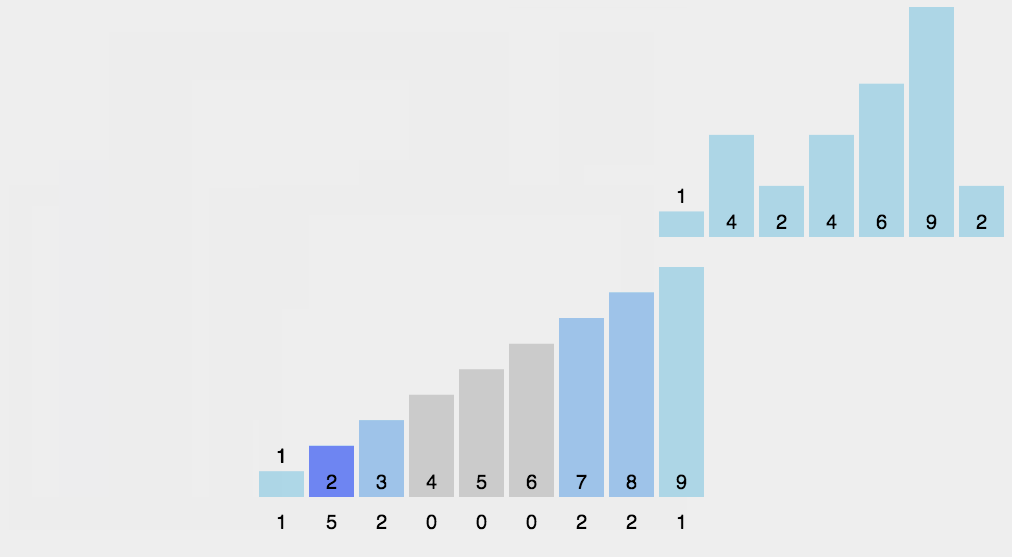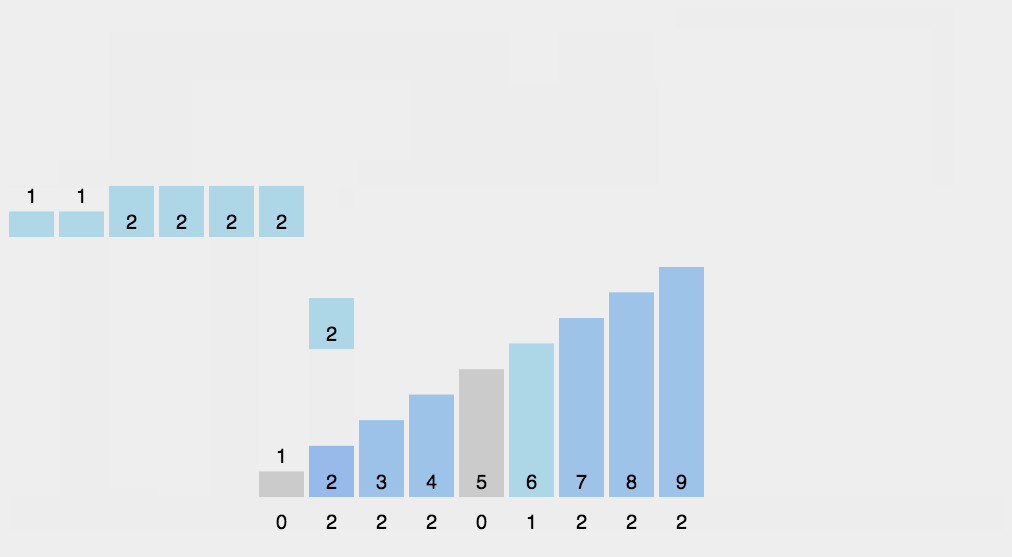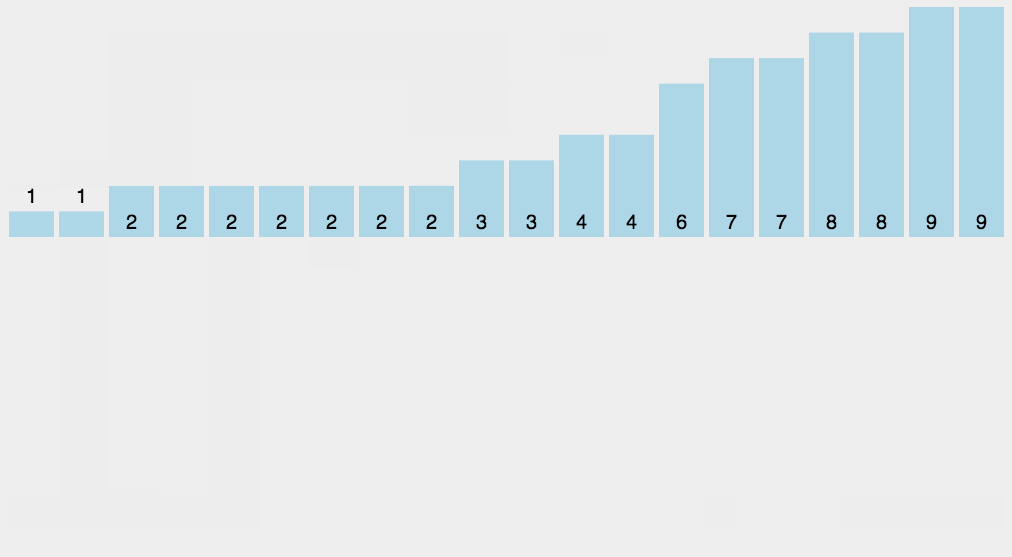
9.3 代码实现

void CountSort(int* a, int n) //计数排序
{
	int max = a[0], min = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;
	int* tmp = (int*)malloc(sizeof(int) * range);
	memset(tmp, 0, sizeof(int) * range);
	for (int i = 0; i < n; i++)
	{
		tmp[a[i] - min]++;
	}
	int k = 0;
	for (int i = 0; i < range; i++)
	{
		while (tmp[i]--)
		{
			a[k++] = i + min;
		}
	}
}

---

十、测试环节

既然写了这么多排序算法，不来比个赛多少有点可惜了

通过下面这段代码，我们来测试一下以上八种排序算法

void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	int* a8 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
		a8[i] = a1[i];
	}
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();
	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();
	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();
	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();
	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
	int end5 = clock();
	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();
	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();
	int begin8 = clock();
	CountSort(a8, N);
	int end8 = clock();
	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);
	printf("CountSort:%d\n", end8 - begin8);
	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
	free(a8);
}

这是10万个数据的测试结果

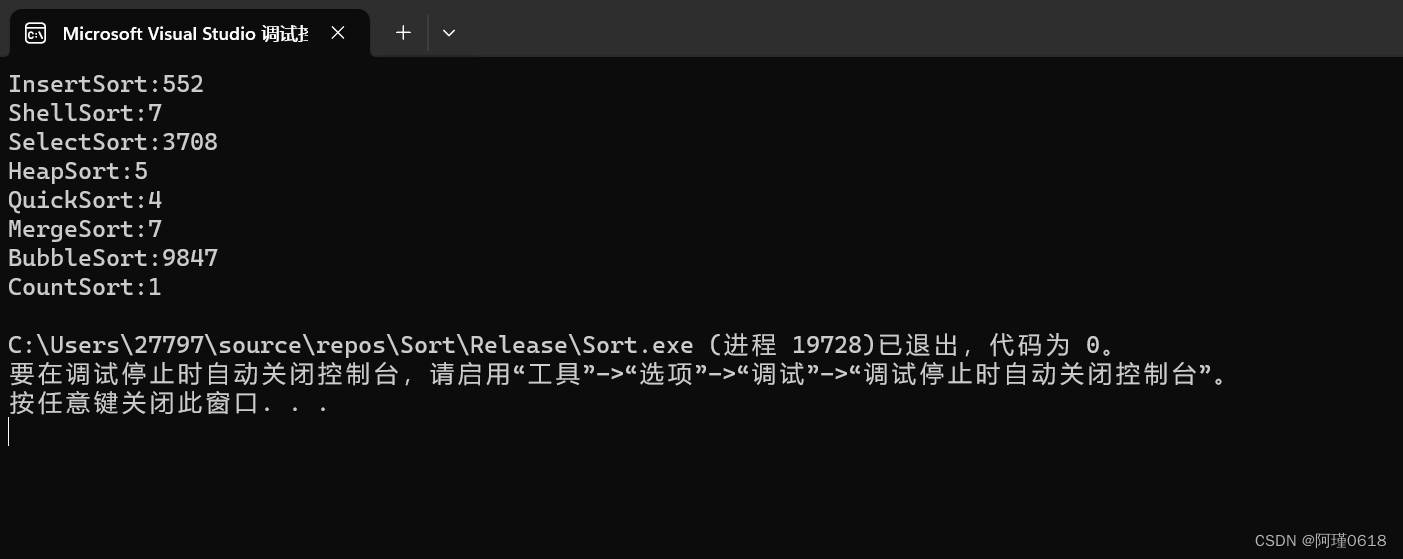
可以显著看到时间复杂度为O(n2)的算法和O(n*logn)的算法之间差距有多大

最后，如果你对不同排序算法的动图有兴趣，可以前往排序（冒泡排序，选择排序，插入排序，归并排序，快速排序，计数排序，基数排序） - VisuAlgohttps://visualgo.net/zh/sorting

如果本文对你有帮助的话就点个赞吧(╹ڡ╹ )

完.