- MySQL中的CASE WHEN语句:用法、示例与解析
- SSL数字证书
- 【微服务】配置Nacos管理SpringBoot配置文件(附解压包)
- Mysql、高斯(Gauss)数据库获取表结构
- vue-create 创建 VUE3项目-创建
- Qt5.14.2 深入理解Qt多线程编程,掌握线程池架构实现高效并发
- 前端vue uni-app仿美团下拉框下拉筛选组件
- Kubernetes(K8s)与虚拟GPU(vGPU):实现高效管理和
- 解决phpstudy无法启动MySQL服务的问题
- 微服务中台架构的设计与实现
- 最详细的Keycloak教程(建议收藏):Keycloak实现手机号、
- JSqlParser的使用
- 实战演练 | 使用 Navicat 进行 MySQL 数据同步
- 如何借助Idea创建多模块的SpringBoot项目
- MySQL默认值(DEFAULT)和MySQL非空约束(NOT NUL
- 如何在CentOS安装SQL Server数据库并实现无公网IP远程连
- Springer Latex投稿(编写中遇到问题及解决方案)
- 基础的正则表达式
- 个人博客建设必备:精选域名和主机的终极攻略
- 亮数据代理IP轻松解决爬虫数据采集痛点
- 前端传输数组类型到后端(附代码)
- Spring AI 使用本地 Ollama Embeddings
- Mybatis之批量更新数据
- Java项目:基于Springboot框架实现的校园求职招聘系统(sp
- navicate远程mysql时报错: connection isbe
- 基于Django的婚纱摄影预约系统设计与实现(Pycharm+Pyth
- 【爬虫实战】python文本分析库——Gensim
- Spring Boot中多线程的使用
- Windows 安装配置 RabbitMQ 详解
- Spring Boot基础 习题题库【附答案】4
背景:GS(Gerchberg-Saxton)在计算全息图、产生光阱方面,对比于直接算法,包括随机相位掩膜法(RM)、棱镜透镜叠加(S)算法,随机叠加(SR)算法,具有光能利用率高的优点,但是和GAA算法一样,都具有一个缺点,即光能的分布上,均匀性不够好。从该缺陷出发,便产生了加权的GS算法(GSW)算法。
本文只讨论纯相位型空间光调制器。设入射在空间光调制器(SLM)的光波为均匀平面波,设振幅为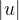 ,则从SLM出射后的光波振幅为
,则从SLM出射后的光波振幅为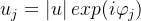 ,其中,
,其中,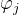 为SLM上第j个像素产生的相移。使用标量衍射理论,得到从SLM上第i行第j列像素的光传播到焦面(focal plane)上第m个光阱处的光振幅为
为SLM上第j个像素产生的相移。使用标量衍射理论,得到从SLM上第i行第j列像素的光传播到焦面(focal plane)上第m个光阱处的光振幅为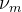

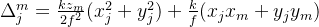
其中,k为波矢,有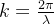 ,λ为波长,
,λ为波长,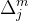 实际上就表示的是位于
实际上就表示的是位于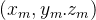 处的光阱经过菲涅耳变换后得到的相位信息,右端包含了其空间频率信息,左端包含了轴向的信息,是一个透镜项。f为傅里叶变换透镜的焦距,d为像素边长,N为像素个数。引入无量纲量
处的光阱经过菲涅耳变换后得到的相位信息,右端包含了其空间频率信息,左端包含了轴向的信息,是一个透镜项。f为傅里叶变换透镜的焦距,d为像素边长,N为像素个数。引入无量纲量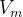

其物理意义通过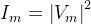 来表示,
来表示,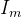 表示第m个光阱能量与总能量之比。计算全息的算法的意义在于对于给定的m个位于
表示第m个光阱能量与总能量之比。计算全息的算法的意义在于对于给定的m个位于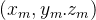 的光阱,或者给定的
的光阱,或者给定的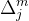 (两者是等效的),给出最优的
(两者是等效的),给出最优的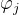 ,使得各个光阱的强度最接近于设计值。对于GS算法、GAA算法这两种迭代算法,其以
,使得各个光阱的强度最接近于设计值。对于GS算法、GAA算法这两种迭代算法,其以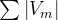 达到最大值为目的,这也是导致其计算产生的光阱强度不均匀的间接原因之一。
达到最大值为目的,这也是导致其计算产生的光阱强度不均匀的间接原因之一。
首先将GS算法的思路作为切入,为了使以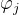 为自变量的函数
为自变量的函数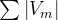 达到最大,
达到最大,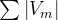 对
对
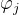 求偏微分得到
求偏微分得到
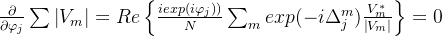
最终得到(原文中用了Hessian矩阵,博主这不太明白QAQ,直接略过了)
![全息图算法:加权Gerchberg-Saxton算法(GSW),第23张 全息图算法:加权Gerchberg-Saxton算法(GSW),\varphi_j=arg\left [ \sum_mexp(i\Delta_j^m)V_m/\left | V_m \right | \right ],第23张](/upload/website_attach/202403/1_8SFEF386X98C888A.jpeg)
而GSW算法,是在该表达式中引入了一个隐式的权重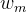 ,表达式变为
,表达式变为
![全息图算法:加权Gerchberg-Saxton算法(GSW),第25张 全息图算法:加权Gerchberg-Saxton算法(GSW),\varphi_j=arg\left [ \sum_mexp(i\Delta_j^m)w_mV_m/\left | V_m \right | \right ],第25张](/upload/website_attach/202403/1_XNN4QAWACWA753Y2.jpeg)
而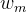 在初次迭代时为1,在第k次迭代中,
在初次迭代时为1,在第k次迭代中, ,其中
,其中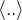 表示求平均。
表示求平均。
在对算法基本原理讲解后,大家可能还是一头雾水的(反正博主是一头雾水的QAQ),github上找到一个python编写的GSW算法源码后,给了我很大启发。如下是我绘制的算法框图,简单明了的讲解了这篇文章想要表达的一个思路。
GSW算法的流程图如图
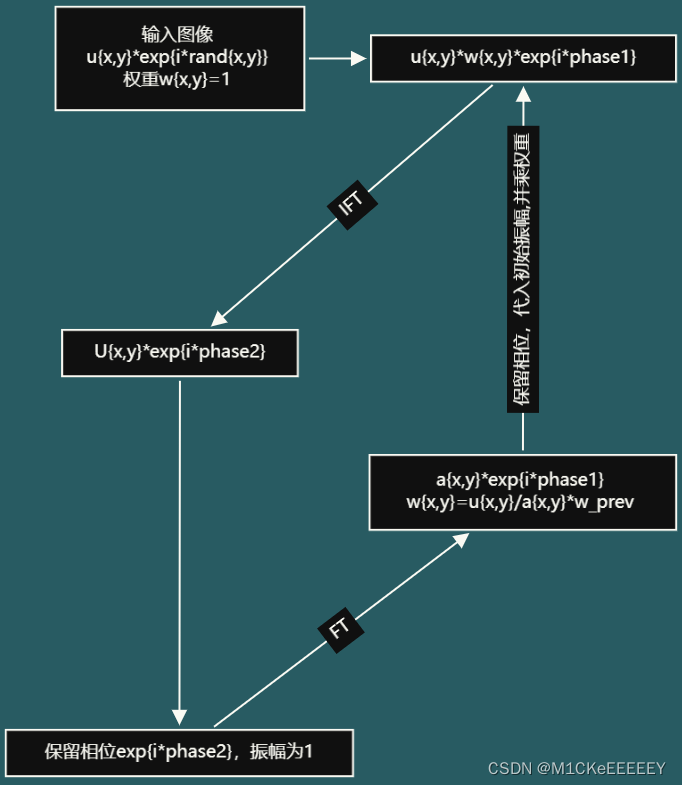
输入图像灰度值作为振幅输入,并对图像每一像素赋予随机相位,作为输入图像。
其与GS算法不同的是,使用了随迭代次数改变的权重系数,即,输入图像中光阱的能量与每次迭代得到的复原图像中光阱能量之比值乘上一次迭代中的权重系数,作为本次迭代的权重。权重的引入,使得全息图还原得到的复原图的光阱能量会朝设计值靠近。
实验:如图所示为设计的图像
如下图为计算得到的计算全息图
下图为使用全息图还原得到的还原图

下图为还原图与原图的相关系数随迭代次数的图像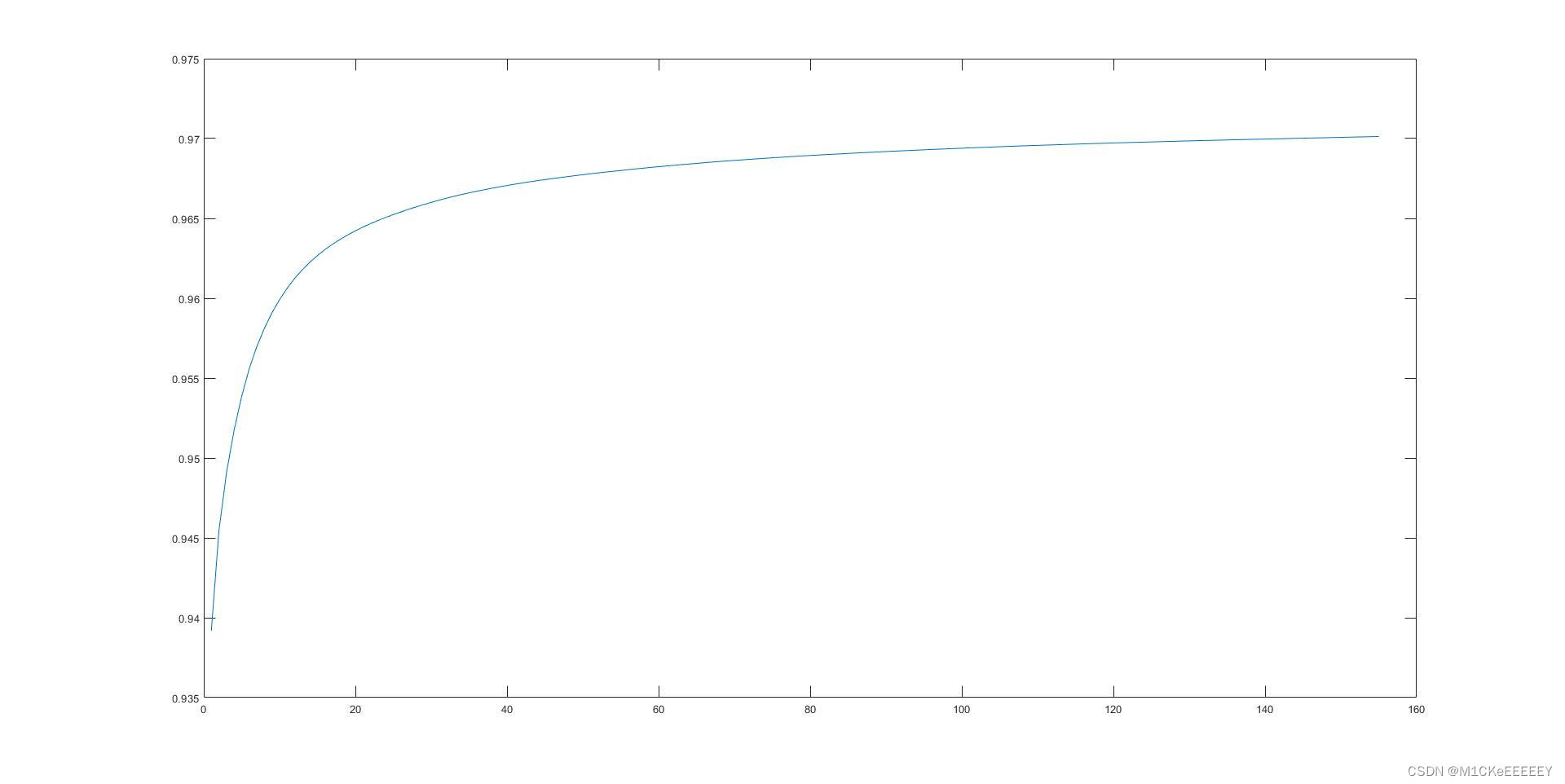
本篇文章中可能还有很多问题,欢迎大家在评论区讨论
参考文献:
[1]Di Leonardo Roberto,Ianni Francesca,Ruocco Giancarlo. Computer generation of optimal holograms for optical trap arrays.[J]. Optics express,2007,15(4).
上一篇:数据结构与算法—顺序表














