- SpringBoot整合Lombok以及各种使用技巧
- AIGC元年大模型发展现状手册
- Spring Boot学习随笔- 集成MyBatis-Plus(二)条
- 使用SM4国密加密算法对Spring Boot项目数据库连接信息以及y
- Matlab方程组拟合【案例源码+视频教程】
- Spring-Kafka 3.0 消费者消费失败处理方案
- MySQL中EXISTS谓词作用及原理
- MVVM架构
- 【Golang入门教程】Go语言变量的声明
- Spring Boot的主要特点
- java.lang.NoClassDefFoundError: org
- 网络编程套接字(1)—网络编程基础
- 个人博客系统|基于Springboot的个人博客系统设计与实现(源码+
- vue使用printJs实现前端打印,以及打印分页实现
- SpringBoot项目中各层的关系和作用
- MongoDB【四】查询与聚合框架
- springboot 如何编写增删改查后端接口,小白极速入门,附完整代
- 标记垃圾,有三种色彩:四千长文带你深入了解三色标记算法
- 智慧工地管理平台APP源码基于物联网、云计算、大数据等技术
- 物流管理系统|基于Springboot的物流管理系统设计与实现(源码+
- sqlplus远程连接oracle ip
- 【云原生系列】云计算概念与架构设计介绍
- 基于Django的婚纱摄影预约系统设计与实现(Pycharm+Pyth
- Java连接PostGreSql
- Springboot 整合 Quartz(定时任务框架)
- 简单爬虫:东方财富网股票数据爬取(20231230)
- 数据结构中的时间复杂度和空间复杂度基础
- 云计算时代的运维: 职业发展方向与岗位选择
- mongodb 安装
- 【Rust】——采用发布配置自定义构建
⭐️ 问题描述
给定一个容器(其体积为 V V V) 和一系列待装载的箱子,容器和箱子的形状都是长方体。问题的目标是要确定一个可行的箱子放置方案使得在满足给定装载约束的情况下,容器中包含的箱子总体积 S S S尽可能的大,即填充率尽可能的大,这里填充率指的是
S / V ∗ 100 % S/ V * 100\% S/V∗100%。可行放置方案要求放置满足如下 3 个条件 👇:
(1) 被装载的箱子必须完全被包含在容器中。 (2) 任何两个被装载的箱子不能互相重叠。 (3) 所有被装载的箱子以与容器平行的方式放置,即不能斜放。
在实际应用中,特定的装箱问题有很多约束,本文仅考虑以下两个约束 👇:
(C1) 方向约束
在许多应用中,箱子的装载有方向约束。也就是说,每个箱子只有它的 1 条或几条边可以竖直放置作为高度。没有此约束的问题可以被简单地视为所有箱子的 3 条边都可以作为高度。
(C2) 稳定性约束
在许多应用中,特别是在交通运输业中,装载必须满足稳定性约束。这意味着每个被装载的箱子必须得到容器底部或者其它箱子的支撑。也就是说,稳定性约束禁止被装载的箱子悬空。也就是说,本文的放置方案必须满足上述两个约束条件。
所有 3 条边相同并且方向约束也相同的箱子被视为同一类型。只有一种箱子类型的装箱问题被称为同构装箱问题。有少数几种箱子类型且每种类型数量较多的装箱问题被称为弱异构装箱问题。强异构装箱问题则有许多箱子类型且每种类型数量较少。本文主要考虑异构装箱问题。
装箱问题是 NP-Hard 问题,采用装箱问题的精确求解算法是不现实的,因此启发式求解方法成为理论研究和实际应用的首选。
⭐️ 基于块装载的基础启发式方法
1. 基本概念和数据结构
为方便下文描述,先介绍一下本文采用的各种数据结构。
1) 基本概念、剩余空间、箱子以及问题实例描述
在装箱问题中,由于所有的物体都是与坐标轴平行的长方体,对它们描述都是通过参考点和各个维度上的边长来指定。所谓参考点就是一个物体的左后下角,也就是其 x , y , z x,y,z x,y,z均最小的点。本文中的装载是在剩余空间中进行的,剩余空间是容器中的未填充长方体空间,其中 x , y , z x,y,z x,y,z描述了它的参考点, l x , l y , l z lx,ly,lz lx,ly,lz描述了它在3个维度上的长度。箱子是问题中被装载的物体,我们用 l x , l y , l z lx,ly,lz lx,ly,lz三个域来描述它3条边的长度。在这里不同朝向的相同箱子被当作不同箱子处理,箱子有一个域 t y p e type type 指定了箱子的真实类型。现在我们可以给出问题实例的描述,三元组 ( c o n t a i n e r , b o x _ l i s t , n u m _ l i s t ) (container,box\_list,num\_list) (container,box_list,num_list)描述了一个三维装箱问题实例,其中 c o n t a i n e r container container是初始剩余空间, b o x _ l i s t box\_list box_list 是一个箱子向量,指定可用于装载的箱子, n u m _ l i s t num\_list num_list则是一个整数向量,描述了每一种类型箱子的数目。
2) 块和块表
块是基于块装载的启发式算法中装载的最小单位,它是包含许多箱子的长方体。块结构中的每个箱子的摆放都满足约束 C1,而且除了最底部的箱子外都满足 C2。块结构用 l x , l y , l z lx,ly,lz lx,ly,lz描述三条边的长, v o l u m e volume volume 描述其中箱子的总体积,整数向量 r e q u i r e _ l i s t require\_list require_list 描述了块对各种类型箱子的需求数。由于块中有空隙,块的顶部有一部分可能由于失去支撑而不能继续放置其它块,我们通过可行放置矩形来描述块的顶部可以继续放置其它块的矩形区域。这里我们仅考虑包括块顶部左后上角的可行放置矩形,以块结构的域 a x , a y ax,ay ax,ay 表示其长宽。块表 b l o c k _ t a b l e block\_table block_table 是预先生成的按块体积降序排列的所有可能块的列表,用于迅速生成指定剩余空间的可行块列表。同时,块表将块生成算法与装载算法分开,使得更换块生成算法变得容易。
3) 剩余空间堆栈和剩余箱子
在基础启发式算法中,剩余空间被组织成堆栈。算法基本过程可描述为:从栈顶取一个剩余空间,若有可行块,按照装载序列选择一个块放置在该空间,将未填充空间切割成新的剩余空间加入堆栈,若无可行块则抛弃此剩余空间,如此反复直至堆栈为空。在此过程中, s p a c e _ s t a c k space\_stack space_stack 表示剩余空间堆栈,整数向量 a v a i l _ l i s t avail\_list avail_list 记录各种剩余箱子的数目。
4) 放置
一个放置是一个剩余空间和块的二元组。例如 ( s p a c e , b l o c k ) (space,block) (space,block) 表示将块 b l o c k block block 放置在剩余空间 s p a c e space space 上。放置是通过将块的参考点和剩余空间的参考点重合得到的。由于算法要保证剩余空间总是被支撑的,而块中除了底部箱子,所有的箱子都满足约束 C1 和 C2,所以每个放置都是满足约束 C1和 C2 的。
5) 部分放置方案
在基本启发式过程中的某一个时刻,剩余空间堆栈和剩余物品构成了一个部分放置方案。
2. 块生成算法
1) 简单块生成
简单块是由同一朝向的同种类型的箱子堆叠而成的,箱子和箱子之间没有空隙,堆叠的结果必须正好形成一个长方体。下图展示了两个简单块的例子,其中 n x , n y , n z nx,ny,nz nx,ny,nz 表示在每个维度上的箱子数。 n x × n y × n z nx×ny×nz nx×ny×nz 则是简单块所需要的总箱子数。
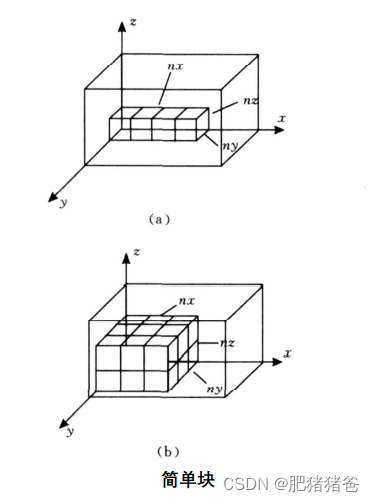
2) 复合块生成
复合块是通过不断复合简单块而得到的,我们定义复合块如下 👇:
(1) 简单块是最基本的复合块。
(2) 有两个复合块 a 和 b。可以按 3 种方式进行复合得到复合块 c :按 x 轴方向复合,按 y 轴方向复合,按 z 轴方向复合。c 的大小是包含 a 和 b 的最小长方体。
下图展示了3种复合方式,其中的虚线描绘的是新复合块的范围。
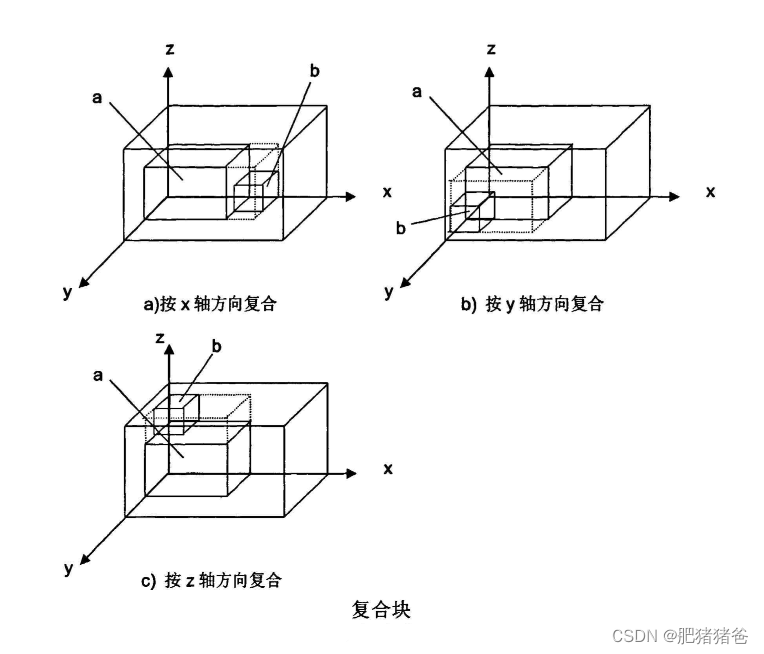
显然,按照前面的定义,复合块的数量将是箱子数目的指数级,而且生成块中可能有很多未利用空间,非常不利于装载. 所以我们对复合块施加一定的限制是必要的,生成的复合块必须满足下面 7 个条件 👇:
(1) 复合块的大小不大于容器的大小。
(2) 复合块中可以有空隙,但它的填充率至少要达到 M I N _ F I L L _ R A T E MIN\_FILL\_RATE MIN_FILL_RATE 。
(3) 受复合块中空隙的影响,复合块顶部有支撑的可行放置矩形可能很小,为了进一步的装载,我们限定可行放置矩形与相应的复合块顶部面积的比至少要达到 M I N _ A R E A _ R A T E MIN\_AREA\_RATE MIN_AREA_RATE。
(4) 为控制复合块的复杂程度,定义复合块的复杂度如下:
简单块的复杂度为 0 0 0,其它复合块的复杂度为其子块的复杂度的最大值加 1 1 1。块结构的 t i m e s times times 域描述了复合块的复杂程度,我们限制生成块的最大复杂次数为 M A X _ T I M E S MAX\_TIMES MAX_TIMES 。
(5) 按 x x x 轴方向、按 y y y 轴方向复合的时候,子块要保证顶部可行放置矩形也能进行复合。在按 z z z 轴方向复合时,子块要保证复合满足约束 C2。具体的复合要求和结果如表 1 所示。
(6) 拥有相同 3 边长度、箱子需求和顶部可行放置矩形的复合块被视为等价块,重复生成的等价块将被忽略。
(7) 在满足以上约束的情况下,块数目仍然可能会很大,我们的生成算法将在块数目达到 M a x B l o c k s MaxBlocks MaxBlocks 时停止生成。
下表描述了考虑稳定性约束情况下具体的复合要求和结果。

在考虑稳定性约束情况下,在块复合的同时,块顶部的可放置矩形也要同时进行复合。由于只有邻接的矩形才能进行复合,顶部可放置矩形的合并情况如下图所示
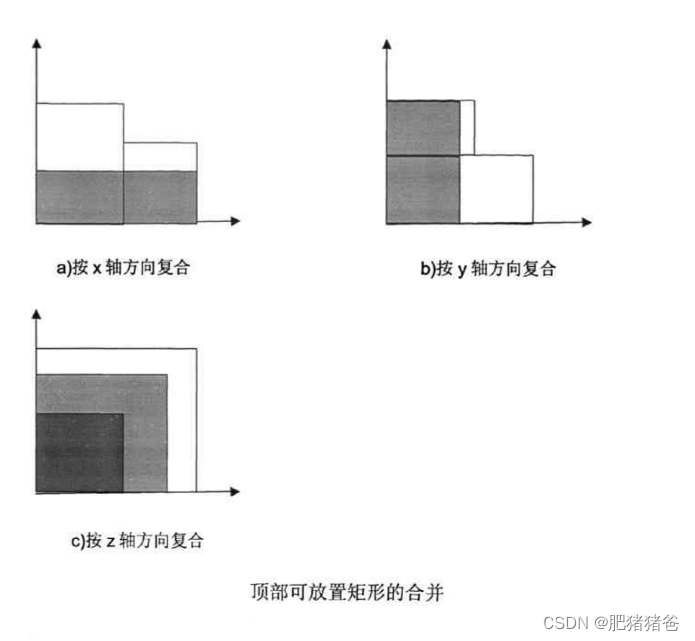
3. 可行块生成
可行块生成算法 g e n _ b l o c k _ l i s t ( s p a c e , a v a i l , b l o c k _ t a b l e ) gen\_block\_list(space,avail,block\_table) gen_block_list(space,avail,block_table) 用于从 b l o c k _ t a b l e block\_table block_table 中获取适合当前剩余空间的可行块列表。该算法扫描 b l o c k _ t a b l e block\_table block_table ,返回所有能放入剩余空间 s p a c e space space 并且 a v a i l avail avail 有足够剩余箱子满足 r e q u i r e require require 的块。由于 b l o c k _ t a b l e block\_table block_table 是按块中箱子总体积降序排列的,返回的 b l o c k _ l i s t block\_list block_list 也是按箱子总体积降序排列的。
4. 空间切割和空间转移
在每个装载阶段一个剩余空间被装载,装载分为两种情况:有可行块,无可行块。在有可行块时,算法按照块选择算法选择可行块,然后将未填充空间切割成新的剩余空间。在无可行块时,当前剩余空间被抛弃,若其中的一部分空间可以被并入当前堆栈中的其他空间,则进行空间转移重新利用这些空间。下图显示了在考虑稳定性约束剩余空间与块结合成为放置以后的状态。未填充空间将被按照不同情况,沿着块的三个面被分成三个剩余空间。需要注意的是,在考虑稳定性约束时,由于要保证所有剩余空间受到足够的支撑, z z z 轴上的新剩余空间在切割的时候必须沿着所选块的顶部可放置矩形进行。因此,块顶部的可放置矩形确定了一个新的剩余空间 s p a c e Z spaceZ spaceZ ,其余的两个剩余空间为x轴方向上的 s p a c e X spaceX spaceX 和 y y y 轴方向上的 s p a c e Y spaceY spaceY ,所以只有两种切割方法。
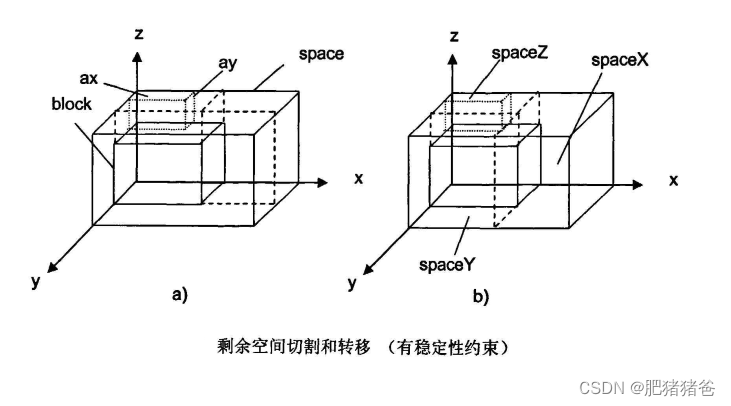
如下图所示,各种切割方式本质上的不同就在于可转移空间的归属。我们希望在切割过程中尽量保证空间完整性,而衡量空间完整性的方法有很多,本文选择的策略是另切割出的剩余空间尽可能的大。这里大小的判定以剩余空间在放置块以后在 x x x 轴、 v v v 轴和 z z z 轴上的剩余长度 m x mx mx、 m y my my、 m z mz mz 作为度量,将可转移空间分给剩余量较大的方向上的新空间。算法中 g e n _ r e s i d u a l _ s p a c e ( s p a c e , b l o c k ) gen\_residual\_space(space,block) gen_residual_space(space,block) 执行未填充空间的切割,其返回的剩余空间 s p a c e X spaceX spaceX、 s p a c e Y spaceY spaceY 、 s p a c e Z spaceZ spaceZ 按照 m x mx mx 、 m y my my、 m z mz mz 的从小到大排列,并确保最后入栈的是包含可转移空间的剩余空间。
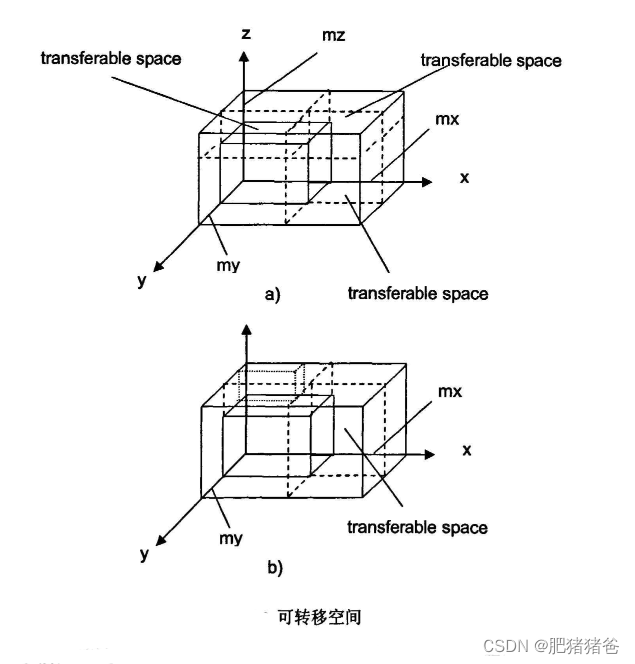
下图列出了在考虑稳定性的情况下,剩余空间的切割方式以及三个空间的入栈顺序。

由于切割算法保证了包含可转移空间的剩余空间后入栈,所以其必然被先装载,若在装载过程中可行块列表为空,栈顶空间中的可转移空间可以被转移给剩余空间堆栈中来自同一次切割的其他空间以重新利用。因此,我们可以通过重新切割未填充空间来达到再次利用可转移空间的目的,算法中的 t r a n s f e r _ s p a c e ( s p a c e , s p a c e _ s t a c k ) transfer\_space(space, space\_stack) transfer_space(space,space_stack) 就是执行这样的任务,此过程判定当前剩余空间与栈顶的一个或两个剩余空间是否是由同一次切割而产生的,若是则将可转移空间转给相应的一个或两个剩余空间。
5. 块的选择算法
块选择问题可以描述为,给定当前的部分放置方案,如何选择最优的块,使得最终取得的填充率最高
1) 整体流程
遍历整个可行块列表,尝试放置当前块到当前部分放置方案,然后用某种方式评估此状态,并将此评估值作为被选块的适应度,最终选取适应度最高的块作为结果。
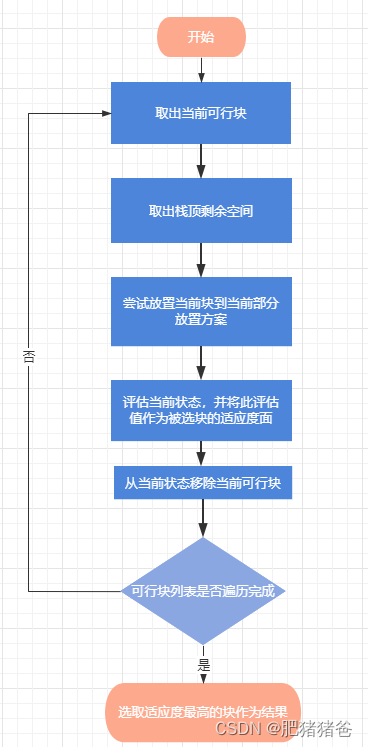
2) 块放置和块移除算法
块放置算法完成的工作包括将块和栈顶空间结合成一个放置加入当前放置方案,移除栈顶空间,扣除已使用物品,然后切割未填充空间并加入剩余空间堆栈。
块移除算法完成的工作包括从当前部分放置方案中移除当前块所属的放置,恢复已使用物品,移除空间堆栈栈顶的三个切割出来的剩余空间,并将已使用剩余空间重新插入栈顶。
3) 补全算法
除了块放置和块移除算法,另一个极其重要的算法是部分放置方案补全算法。我们知道,评估当前的部分放置方案好坏的最直接的方法是用某种方式补全它,并以最终结果的填充率作为当前状态的评估值。该算法实际上是整体基本启发式算法的一个简化版本,区别在于每个装载阶段算法都选择可行块列表中体积最大的块进行放置。由于可行块列表已经按照体积降序排列,实际上算法选择的块总是列表的第一个元素。算法不改变输入的部分放置方案,只是把最终补全的结果记录在此状态的 v o l u m e _ c o m p l e t e volume\_complete volume_complete 域作为该状态的评估值。
4) 贪心算法
在块的选择算法过程中,也可以采用贪心算法,直接返回填充体积最大的块,由于可行块列表已经按照体积降序排列,实际上算法选择的块总是列表的第一个元素。
5) 带深度限制的深度优先搜索算法
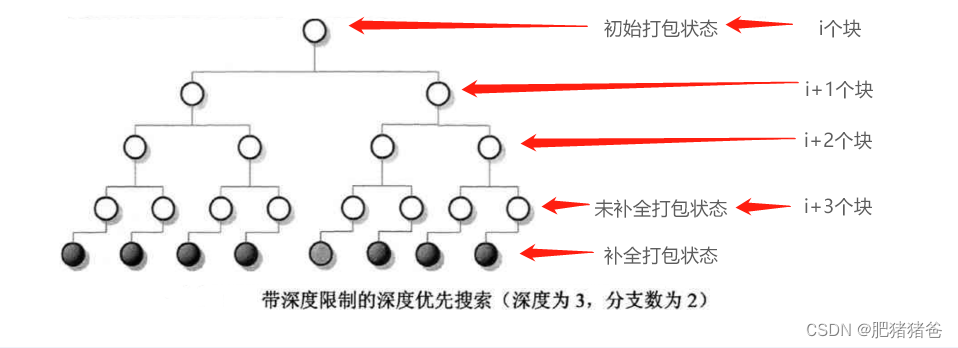
除了贪心算法和简单的补全算法,另一个很容易想到的方法是进行深度或广度优先搜索扩展当前放置方案,然后在叶子节点使用补全算法来评估叶节点的好坏,最终以搜索树中最好的一个叶子节点的评估值作为当前状态的评估。但是,由于搜索过程中,每一个节点都有大量分支,采用宽度优先搜索需要海量的空间,因此是不现实的。实际应用中,一般采用的是带深度限制的深度优先搜索算法,通过深度来限制最多放置的块的数目。另外,由于每个阶段可行块列表包含大量的块,算法往往也限制每个节点的最大分支数。本文采用深度优先搜索算法扩展当前放置方案,算法的输入为一个部分放置方案,深度限制和最大分支数。该算法从一个部分放置方案出发,递归的尝试可行块列表中的块,在到达深度限制的时候调用补全函数得到当前方案的评估值,并记录整个搜索过程找到的最优的评估值作为输入部分放置方案的评估。
这里特别注意的是搜索深度代表通过深度优先搜索放置的块的最大个数。
如下图所示,节点生成两个子节点,直到节点深度为3时使用补全算法取得当前状态的评估值,最后采用整个算法中最好的结果作为算法的最终结果。图中,白色节点表示搜索时遍历的内部节点,黑色节点表示用补全算法计算出的节点,而灰色表示最
终选择的最优节点。
⭐️ 程序及运行结果(笔者python运行环境为python3.7)
import copy
from itertools import product
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np
# 复合块的最小填充率
MIN_FILL_RATE = 0.9
# 可行放置矩形与相应复合块顶部面积比的最小值
MIN_AREA_RATE = 0.9
# 复合块最大复杂度
MAX_TIMES = 2
# 搜索树深度
MAX_DEPTH = 3
# 搜索树节点分支数
MAX_BRANCH = 2
# 临时的最优放置方案
tmp_best_ps = None
# 栈数据结构,用于存储剩余空间
class Stack:
def __init__(self):
self.data = []
def empty(self):
return len(self.data) == 0
def not_empty(self):
return len(self.data) > 0
def pop(self):
return self.data.pop() if len(self.data) > 0 else None
def push(self, *items):
for item in items:
self.data.append(item)
def top(self):
return self.data[len(self.data) - 1] if len(self.data) > 0 else None
def clear(self):
self.data.clear()
def size(self):
return len(self.data)
# 箱子类
class Box:
def __init__(self, lx, ly, lz, type=0):
# 长
self.lx = lx
# 宽
self.ly = ly
# 高
self.lz = lz
# 类型
self.type = type
def __str__(self):
return "lx: {}, ly: {}, lz: {}, type: {}".format(self.lx, self.ly, self.lz, self.type)
# 剩余空间类
class Space:
def __init__(self, x, y, z, lx, ly, lz, origin=None):
# 坐标
self.x = x
self.y = y
self.z = z
# 长
self.lx = lx
# 宽
self.ly = ly
# 高
self.lz = lz
# 表示从哪个剩余空间切割而来
self.origin = origin
def __str__(self):
return "x:{},y:{},z:{},lx:{},ly:{},lz:{}".format(self.x, self.y, self.z, self.lx, self.ly, self.lz)
def __eq__(self, other):
return self.x == other.x and self.y == other.y and self.z == other.z and self.lx == other.lx and self.ly == other.ly and self.lz == other.lz
# 装箱问题类
class Problem:
def __init__(self, container: Space, box_list=[], num_list=[]):
# 容器
self.container = container
# 箱子列表
self.box_list = box_list
# 箱子对应的数量
self.num_list = num_list
# 块类
class Block:
def __init__(self, lx, ly, lz, require_list=[], children=[], direction=None):
# 长
self.lx = lx
# 宽
self.ly = ly
# 高
self.lz = lz
# 需要的物品数量
self.require_list = require_list
# 体积
self.volume = 0
# 子块列表,简单块的子块列表为空
self.children = children
# 复合块子块的合并方向
self.direction = direction
# 顶部可放置矩形尺寸
self.ax = 0
self.ay = 0
# 复杂度,复合次数
self.times = 0
# 适应度,块选择时使用
self.fitness = 0
def __str__(self):
return "lx: %s, ly: %s, lz: %s, volume: %s, ax: %s, ay: %s, times:%s, fitness: %s, require: %s, children: " \
"%s, direction: %s" % (self.lx, self.ly, self.lz, self.volume, self.ax, self.ay, self.times, self.fitness, self.require_list, self.children, self.direction)
def __eq__(self, other):
return self.lx == other.lx and self.ly == other.ly and self.lz == other.lz and self.ax == other.ax and self.ay == self.ay and (np.array(self.require_list) == np.array(other.require_list)).all()
def __hash__(self):
return hash(",".join([str(self.lx), str(self.ly), str(self.lz), str(self.ax), str(self.ay), ",".join([str(r) for r in self.require_list])]))
# 放置类
class Place:
def __init__(self, space: Space, block: Block):
# 空间
self.space = space
# 块
self.block = block
def __eq__(self, other):
return self.space == other.space and self.block == other.block
# 装箱状态类
class PackingState:
def __init__(self, plan_list=[], space_stack: Stack = Stack(), avail_list=[]):
# 已生成的装箱方案列表
self.plan_list = plan_list
# 剩余空间堆栈
self.space_stack = space_stack
# 剩余可用箱体数量
self.avail_list = avail_list
# 已装载物品总体积
self.volume = 0
# 最终装载物品的总体积的评估值
self.volume_complete = 0
# 合并块时通用校验项目
def combine_common_check(combine: Block, container: Space, num_list):
# 合共块尺寸不得大于容器尺寸
if combine.lx > container.lx:
return False
if combine.ly > container.ly:
return False
if combine.lz > container.lz:
return False
# 合共块需要的箱子数量不得大于箱子总的数量
if (np.array(combine.require_list) > np.array(num_list)).any():
return False
# 合并块的填充体积不得小于最小填充率
if combine.volume / (combine.lx * combine.ly * combine.lz) < MIN_FILL_RATE:
return False
# 合并块的顶部可放置矩形必须足够大
if (combine.ax * combine.ay) / (combine.lx * combine.ly) < MIN_AREA_RATE:
return False
# 合并块的复杂度不得超过最大复杂度
if combine.times > MAX_TIMES:
return False
return True
# 合并块时通用合并项目
def combine_common(a: Block, b: Block, combine: Block):
# 合并块的需求箱子数量
combine.require_list = (np.array(a.require_list) + np.array(b.require_list)).tolist()
# 合并填充体积
combine.volume = a.volume + b.volume
# 构建父子关系
combine.children = [a, b]
# 合并后的复杂度
combine.times = max(a.times, b.times) + 1
# 生成简单块
def gen_simple_block(container, box_list, num_list):
block_table = []
for box in box_list:
for nx in np.arange(num_list[box.type]) + 1:
for ny in np.arange(num_list[box.type] / nx) + 1:
for nz in np.arange(num_list[box.type] / nx / ny) + 1:
if box.lx * nx <= container.lx and box.ly * ny <= container.ly and box.lz * nz <= container.lz:
# 该简单块需要的立体箱子数量
requires = np.full_like(num_list, 0)
requires[box.type] = nx * ny * nz
# 简单块
block = Block(box.lx * nx, box.ly * ny, box.lz * nz, requires)
# 顶部可放置矩形
block.ax = box.lx * nx
block.ay = box.ly * ny
# 简单块填充体积
block.volume = box.lx * nx * box.ly * ny * box.lz * nz
# 简单块复杂度
block.times = 0
block_table.append(block)
return sorted(block_table, key=lambda x: x.volume, reverse=True)
# 生成复合块
def gen_complex_block(container, box_list, num_list):
# 先生成简单块
block_table = gen_simple_block(container, box_list, num_list)
for times in range(MAX_TIMES):
new_block_table = []
# 循环所有简单块,两两配对
for i in np.arange(0, len(block_table)):
# 第一个简单块
a = block_table[i]
for j in np.arange(0, len(block_table)):
# 简单块不跟自己复合
if j == i:
continue
# 第二个简单块
b = block_table[j]
# 复杂度满足当前复杂度
if a.times == times or b.times == times:
c = Block(0, 0, 0)
# 按x轴方向复合
if a.ax == a.lx and b.ax == b.lx and a.lz == b.lz:
c.direction = "x"
c.ax = a.ax + b.ax
c.ay = min(a.ay, b.ay)
c.lx = a.lx + b.lx
c.ly = max(a.ly, b.ly)
c.lz = a.lz
combine_common(a, b, c)
if combine_common_check(c, container, num_list):
new_block_table.append(c)
continue
# 按y轴方向复合
if a.ay == a.ly and b.ay == b.ly and a.lz == b.lz:
c.direction = "y"
c.ax = min(a.ax, b.ax)
c.ay = a.ay + b.ay
c.lx = max(a.lx, b.lx)
c.ly = a.ly + b.ly
c.lz = a.lz
combine_common(a, b, c)
if combine_common_check(c, container, num_list):
new_block_table.append(c)
continue
# 按z轴方向复合
if a.ax >= b.lx and a.ay >= b.ly:
c.direction = "z"
c.ax = b.ax
c.ay = b.ay
c.lx = a.lx
c.ly = a.ly
c.lz = a.lz + b.lz
combine_common(a, b, c)
if combine_common_check(c, container, num_list):
new_block_table.append(c)
continue
# 加入新生成的复合块
block_table = block_table + new_block_table
# 去重,拥有相同三边长度、物品需求和顶部可放置矩形的复合块被视为等价块,重复生成的等价块将被忽略
block_table = list(set(block_table))
# 按填充体积对复合块进行排序
return sorted(block_table, key=lambda x: x.volume, reverse=True)
# 生成可行块列表
def gen_block_list(space: Space, avail, block_table):
block_list = []
for block in block_table:
# 块中需要的箱子需求数量必须小于当前待装箱的箱子数量
# 块的尺寸必须小于放置空间尺寸
if (np.array(block.require_list) <= np.array(avail)).all() and \
block.lx <= space.lx and block.ly <= space.ly and block.lz <= space.lz:
block_list.append(block)
return block_list
# 裁切出新的剩余空间(有稳定性约束)
def gen_residual_space(space: Space, block: Block, box_list=[]):
# 三个维度的剩余尺寸
rmx = space.lx - block.lx
rmy = space.ly - block.ly
rmz = space.lz - block.lz
# 三个新裁切出的剩余空间(按入栈顺序依次返回)
if rmx >= rmy:
# 可转移空间归属于x轴切割空间
drs_x = Space(space.x + block.lx, space.y, space.z, rmx, space.ly, space.lz, space)
drs_y = Space(space.x, space.y + block.ly, space.z, block.lx, rmy, space.lz, space)
drs_z = Space(space.x, space.y, space.z + block.lz, block.ax, block.ay, rmz, None)
return drs_z, drs_y, drs_x
else:
# 可转移空间归属于y轴切割空间
drs_x = Space(space.x + block.lx, space.y, space.z, rmx, block.ly, space.lz, space)
drs_y = Space(space.x, space.y + block.ly, space.z, space.lx, rmy, space.lz, space)
drs_z = Space(space.x, space.y, space.z + block.lz, block.ax, block.ay, rmz, None)
return drs_z, drs_x, drs_y
# 空间转移
def transfer_space(space: Space, space_stack: Stack):
# 仅剩一个空间的话,直接弹出
if space_stack.size() <= 1:
space_stack.pop()
return None
# 待转移空间的原始空间
discard = space
# 目标空间
space_stack.pop()
target = space_stack.top()
# 将可转移的空间转移给目标空间
if discard.origin is not None and target.origin is not None and discard.origin == target.origin:
new_target = copy.deepcopy(target)
# 可转移空间原先归属于y轴切割空间的情况
if discard.lx == discard.origin.lx:
new_target.ly = discard.origin.ly
# 可转移空间原来归属于x轴切割空间的情况
elif discard.ly == discard.origin.ly:
new_target.lx = discard.origin.lx
else:
return None
space_stack.pop()
space_stack.push(new_target)
# 返回未发生转移之前的目标空间
return target
return None
# 还原空间转移
def transfer_space_back(space: Space, space_stack: Stack, revert_space: Space):
space_stack.pop()
space_stack.push(revert_space)
space_stack.push(space)
# 块放置算法
def place_block(ps: PackingState, block: Block):
# 栈顶剩余空间
space = ps.space_stack.pop()
# 更新可用箱体数目
ps.avail_list = (np.array(ps.avail_list) - np.array(block.require_list)).tolist()
# 更新放置计划
place = Place(space, block)
ps.plan_list.append(place)
# 更新体积利用率
ps.volume = ps.volume + block.volume
# 压入新的剩余空间
cuboid1, cuboid2, cuboid3 = gen_residual_space(space, block)
ps.space_stack.push(cuboid1, cuboid2, cuboid3)
# 返回临时生成的放置
return place
# 块移除算法
def remove_block(ps: PackingState, block: Block, place: Place, space: Space):
# 还原可用箱体数目
ps.avail_list = (np.array(ps.avail_list) + np.array(block.require_list)).tolist()
# 还原排样计划
ps.plan_list.remove(place)
# 还原体积利用率
ps.volume = ps.volume - block.volume
# 移除在此之前裁切出的新空间
for _ in range(3):
ps.space_stack.pop()
# 还原之前的空间
ps.space_stack.push(space)
# 补全放置方案
def complete(ps: PackingState, block_table):
# 不对当前的放置状态进行修改
tmp = copy.deepcopy(ps)
while tmp.space_stack.not_empty():
# 栈顶空间
space = tmp.space_stack.top()
# 可用块列表
block_list = gen_block_list(space, ps.avail_list, block_table)
if len(block_list) > 0:
# 放置块
place_block(tmp, block_list[0])
else:
# 空间转移
transfer_space(space, tmp.space_stack)
# 补全后的使用体积
ps.volume_complete = tmp.volume
# 带深度限制的深度优先搜索算法
def depth_first_search(ps: PackingState, depth, branch, block_table):
global tmp_best_ps
if depth != 0:
space = ps.space_stack.top()
block_list = gen_block_list(space, ps.avail_list, block_table)
if len(block_list) > 0:
# 遍历所有分支
for i in range(min(branch, len(block_list))):
# 放置块
place = place_block(ps, block_list[i])
# 放置下一个块
depth_first_search(ps, depth - 1, branch, block_table)
# 移除刚才添加的块
remove_block(ps, block_list[i], place, space)
else:
# 转移空间
old_target = transfer_space(space, ps.space_stack)
if old_target:
# 放置下一个块
depth_first_search(ps, depth, branch, block_table)
# 还原转移空间
transfer_space_back(space, ps.space_stack, old_target)
else:
# 补全该方案
complete(ps, block_table)
# 更新最优解
if ps.volume_complete > tmp_best_ps.volume_complete:
tmp_best_ps = copy.deepcopy(ps)
# 评价某个块
def estimate(ps: PackingState, block_table, search_params):
# 空的放置方案
global tmp_best_ps
# tmp_best_ps = PackingState()
tmp_best_ps = PackingState([], Stack(), [])
# 开始深度优先搜索
depth_first_search(ps, MAX_DEPTH, MAX_BRANCH, block_table)
return tmp_best_ps.volume_complete
# 查找下一个可行块
def find_next_block(ps: PackingState, block_list, block_table, search_params):
# 最优适应度
best_fitness = 0
# 初始化最优块为第一个块(填充体积最大的块)
best_block = block_list[0]
# 遍历所有可行块
for block in block_list:
# 栈顶空间
space = ps.space_stack.top()
# 放置块
place = place_block(ps, block)
# 评价值
fitness = estimate(ps, block_table, search_params)
# 移除刚才添加的块
remove_block(ps, block, place, space)
# 更新最优解
if fitness > best_fitness:
best_fitness = fitness
best_block = block
return best_block
# # 也可以采用贪心算法,直接返回填充体积最大的块
# return block_list[0]
# 递归构建箱体坐标,用于绘图
def build_box_position(block, init_pos, box_list):
# 遇到简单块时进行坐标计算
if len(block.children) <= 0 and block.times == 0:
# 箱体类型索引
box_idx = (np.array(block.require_list) > 0).tolist().index(True)
if box_idx > -1:
# 所需箱体
box = box_list[box_idx]
# 箱体的相对坐标
nx = block.lx / box.lx
ny = block.ly / box.ly
nz = block.lz / box.lz
x_list = (np.arange(0, nx) * box.lx).tolist()
y_list = (np.arange(0, ny) * box.ly).tolist()
z_list = (np.arange(0, nz) * box.lz).tolist()
# 箱体的绝对坐标
dimensions = (np.array([x for x in product(x_list, y_list, z_list)]) + np.array([init_pos[0], init_pos[1], init_pos[2]])).tolist()
return sorted([d + [box.lx, box.ly, box.lz] for d in dimensions], key=lambda x: (x[0], x[1], x[2]))
return []
pos = []
for child in block.children:
pos += build_box_position(child, (init_pos[0], init_pos[1], init_pos[2]), box_list)
# 根据子块的复合方向,确定下一个子块的左后下角坐标
if block.direction == "x":
init_pos = (init_pos[0] + child.lx, init_pos[1], init_pos[2])
elif block.direction == "y":
init_pos = (init_pos[0], init_pos[1] + child.ly, init_pos[2])
elif block.direction == "z":
init_pos = (init_pos[0], init_pos[1], init_pos[2] + child.lz)
return pos
# 绘制立方体边框
def plot_linear_cube(ax, x, y, z, dx, dy, dz, color='red', linestyle=None):
xx = [x, x, x+dx, x+dx, x]
yy = [y, y+dy, y+dy, y, y]
kwargs = {"alpha": 1, "color": color, "linewidth": 2.5, "zorder": 2}
if linestyle:
kwargs["linestyle"] = linestyle
ax.plot3D(xx, yy, [z]*5, **kwargs)
ax.plot3D(xx, yy, [z+dz]*5, **kwargs)
ax.plot3D([x, x], [y, y], [z, z+dz], **kwargs)
ax.plot3D([x, x], [y+dy, y+dy], [z, z+dz], **kwargs)
ax.plot3D([x+dx, x+dx], [y+dy, y+dy], [z, z+dz], **kwargs)
ax.plot3D([x+dx, x+dx], [y, y], [z, z+dz], **kwargs)
# 立方体
def cuboid_data2(o, size=(1, 1, 1)):
X = [[[0, 1, 0], [0, 0, 0], [1, 0, 0], [1, 1, 0]],
[[0, 0, 0], [0, 0, 1], [1, 0, 1], [1, 0, 0]],
[[1, 0, 1], [1, 0, 0], [1, 1, 0], [1, 1, 1]],
[[0, 0, 1], [0, 0, 0], [0, 1, 0], [0, 1, 1]],
[[0, 1, 0], [0, 1, 1], [1, 1, 1], [1, 1, 0]],
[[0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 1, 1]]]
X = np.array(X).astype(float)
for i in range(3):
X[:, :, i] *= size[i]
X += np.array(o)
return X
# 绘制立方体
def plotCubeAt2(positions, sizes=None, colors=None, **kwargs):
if not isinstance(colors, (list, np.ndarray)):
colors = ["C0"] * len(positions)
if not isinstance(sizes, (list, np.ndarray)):
sizes = [(1, 1, 1)] * len(positions)
g = []
for p, s, c in zip(positions, sizes, colors):
g.append(cuboid_data2(p, size=s))
return Poly3DCollection(np.concatenate(g), facecolors=np.repeat(colors, 6), **kwargs)
# 绘制排样结果
def draw_packing_result(problem: Problem, ps: PackingState):
# 绘制结果
fig = plt.figure()
ax1 = mplot3d.Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax1)
# 绘制容器
plot_linear_cube(ax1, 0, 0, 0, problem.container.lx, problem.container.ly, problem.container.lz)
for p in ps.plan_list:
# 箱子位置及尺寸
box_pos = build_box_position(p.block, (p.space.x, p.space.y, p.space.z), problem.box_list)
positions = []
sizes = []
# 箱子颜色
colors = ["yellow"] * len(box_pos)
for bp in sorted(box_pos, key=lambda x: (x[0], x[1], x[2])):
positions.append((bp[0], bp[1], bp[2]))
sizes.append((bp[3], bp[4], bp[5]))
pc = plotCubeAt2(positions, sizes, colors=colors, edgecolor="k")
ax1.add_collection3d(pc)
plt.title('PackingResult')
plt.show()
# plt.savefig('3d_multilayer_search.png', dpi=800)
# 基本启发式算法
def basic_heuristic(is_complex, search_params, problem: Problem):
if is_complex:
# 生成复合块
block_table = gen_complex_block(problem.container, problem.box_list, problem.num_list)
else:
# 生成简单块
block_table = gen_simple_block(problem.container, problem.box_list, problem.num_list)
# 初始化排样状态
ps = PackingState(avail_list=problem.num_list)
# 开始时,剩余空间堆栈中只有容器本身
ps.space_stack.push(problem.container)
# 所有剩余空间均转满,则停止
while ps.space_stack.size() > 0:
space = ps.space_stack.top()
block_list = gen_block_list(space, ps.avail_list, block_table)
if block_list:
# 查找下一个近似最优块
block = find_next_block(ps, block_list, block_table, search_params)
# 弹出顶部剩余空间
ps.space_stack.pop()
# 更新可用物品数量
ps.avail_list = (np.array(ps.avail_list) - np.array(block.require_list)).tolist()
# 更新排样计划
ps.plan_list.append(Place(space, block))
# 更新已利用体积
ps.volume = ps.volume + block.volume
# 压入新裁切的剩余空间
cuboid1, cuboid2, cuboid3 = gen_residual_space(space, block)
ps.space_stack.push(cuboid1, cuboid2, cuboid3)
else:
# 转移剩余空间
transfer_space(space, ps.space_stack)
# 打印剩余箱体和已使用容器的体积
print("ps.avail_list")
print(ps.avail_list)
print(ps.volume)
# 绘制排样结果图
draw_packing_result(problem, ps)
# 主算法
def main():
# 容器
container = Space(0, 0, 0, 10, 10, 10)
# 箱体列表及数量
# 深度优先遍历算法效率较低,可以采用如下测试数据
box_list = [Box(1, 2, 3, 0), Box(4, 5, 5, 1), Box(1, 1, 1, 2), Box(2, 2, 2, 3), Box(4, 5, 2, 4)]
num_list = [3, 4, 3, 2, 1]
# 贪心算法效率较高,可以采用如下测试数据
# box_list = [Box(1, 2, 3, 0), Box(4, 5, 5, 1), Box(1, 1, 1, 2), Box(2, 2, 2, 3), Box(4, 5, 2, 4)]
# num_list = [11, 4, 5, 8, 6]
# 问题
problem = Problem(container, box_list, num_list)
search_params = dict()
# 具体计算
basic_heuristic(True, search_params, problem)
if __name__ == "__main__":
main()
贪心算法运行结果如下(箱子数量较多的情况):
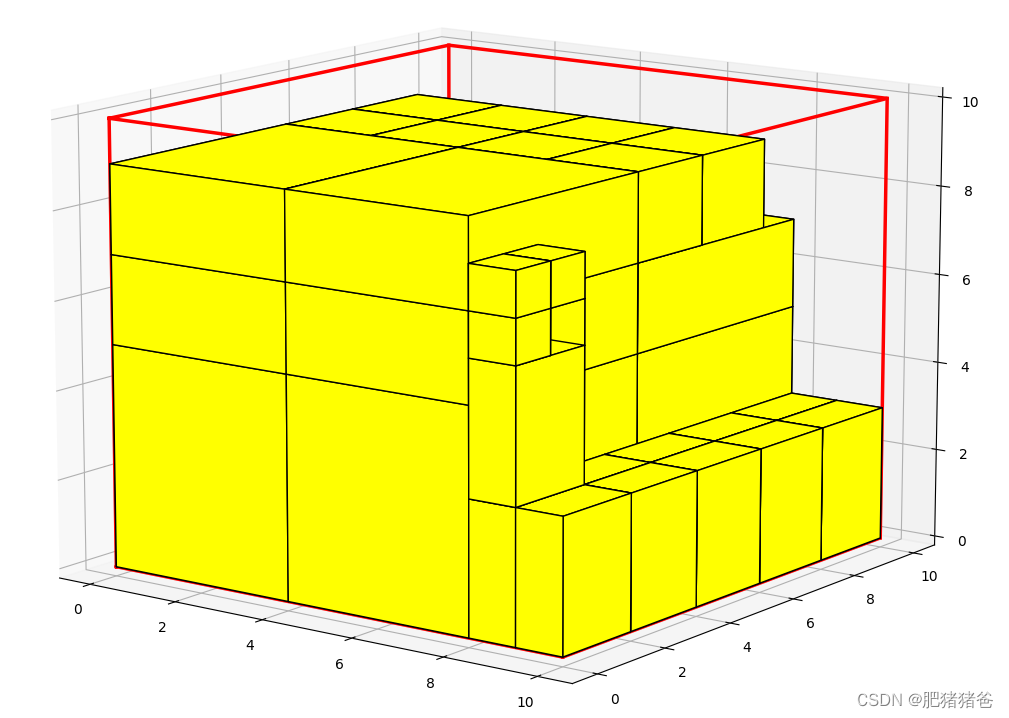
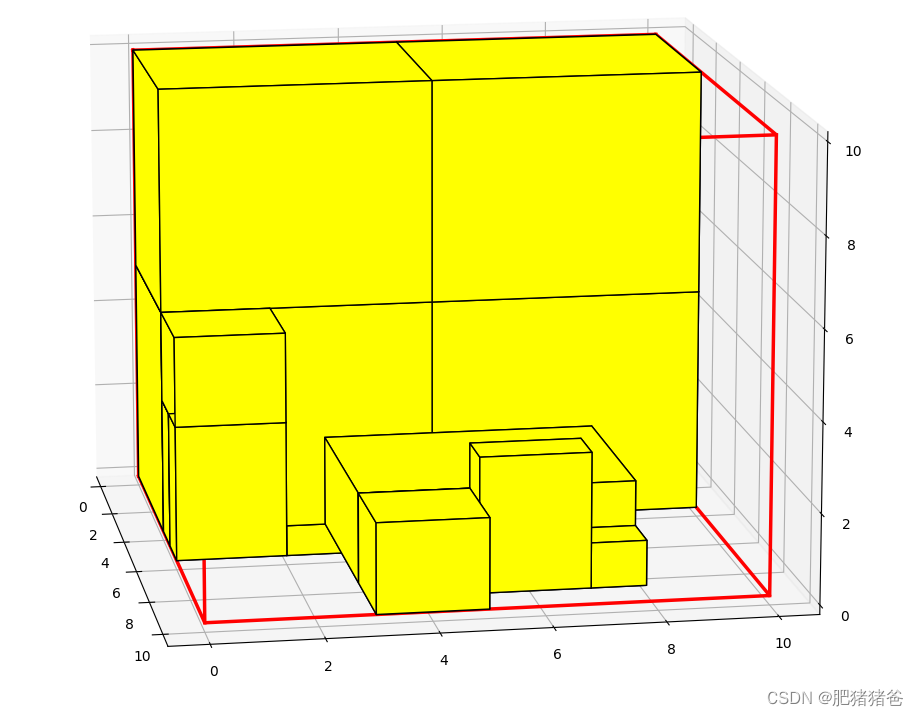
带深度限制的深度优先搜索算法运行结果如下(箱子数量较少的情况):
⭐️ 写在最后
本文理论部分摘自厦门大学的硕士论文《求解三维装箱问题的启发式分层搜索算法》,论文作者和导师都很牛,读者可以自行百度获取论文原文😏。
深度优先搜索算法运行效率比较低下,有兴趣和实力的读者可以对此做进一步的优化,若想到了idea,欢迎留言分享啊🍉
笔者水平有限,若有不对的地方欢迎评论指正














