- 【微服务】接口幂等性常用解决方案
- php
- 使用gradle创建spring项目时报错Could not reso
- Kafka(Windows)安装配置启动(常见错误扫雷)教程
- 创建Maven项目
- C#ORM框架SqlSugar安装及使用(以MySql、sqlite为
- 【MySQL】设置字符集与排序规则
- 使用Docker搭建YesPlayMusic网易云音乐播放器并发布至公
- ELFK日志分析系统之搭建ELF+Filebeaat+Zookeepe
- Golang 开发实战day08 - Multiple Return
- Springboot各版本与Java JDK的对应关系及JDK商用版本
- 数据结构 -> 时间复杂度和空间复杂度的计算(做题助推器)
- Spring Cloud - 手写 Gateway 源码,实现自定义局
- 关于Node.js作为后端的入门教程
- 全国主要城市建筑轮廓(含层高)矢量数据分享及最新AI提取建筑分布方法介
- 【Consul】基于Golang实现Consul服务的注册、注销、修改
- 基于springboot的酒店管理系统论文
- Linux部署Sonarqube+Gogs+Jenkins(一)
- IDEA实现ssh远程连接本地Linux服务器
- 微信小程序使用PHP调用后台mysql数据库-小白版
- org.apache.tomcat.util.http.fileupl
- Spring Boot:基础配置
- SQL Server数据库日志查看若已满需要清理的三种解决方案
- Docker - 基本概念、与虚拟机的区别、架构、镜像操作、容器操作、
- SpringBlade dict-bizlist SQL 注入漏洞复现
- 【爬虫实战】使用Python获取花粉俱乐部中Mate60系列的用户发帖
- sqlplus远程连接oracle ip
- mysql的IN查询优化
- 【python】flask执行上下文context,请求上下文和应用上
- NL2SQL 自然语言生成SQL方案汇总
EMD是时频分析常用的一种信号处理方式,EMD经过发展到现在也有很多不同的发展,本文总结了已知的各种优化和变种。
分类:
EMD(经验模态分解):基本模态分解
EEMD(集合经验模态分解):EMD+白噪声
CEEMD(互补集合经验模态分解):加正负成对的辅助白噪声
CEEMDAN(完全自适应噪声集合经验模态分解):分解过程加白噪声经EMD分解得到的各阶IMF分量
ESMD(极点对称模态分解):外部包络线插值改内部极点对称插值
VMD(变分模态分解): 可将时间序列数据分解为一系列具有有限带宽的本征模态函数(IMF),可自适应更新各IMF的最优中心频率和带宽。
LMD(局域均值分解):PF 分量分解,采用平滑处理的方法形成局部均值函数和局域包络函数,因此可以避免 EMD 方法中采用三次样条函数形成上下包络线时产生的过包络、欠包络现象。
RLMD(鲁棒性局部均值分解):可以处理LMD中的边界条件、包络估计和筛选停止准则
EMD(经验模态分解):
EMD在非线性非平稳信号分析中具有显著优势。与传统时频分析技术相比,EMD无需选择基函数,其分解基于信号本身极值点的分布。
例如:
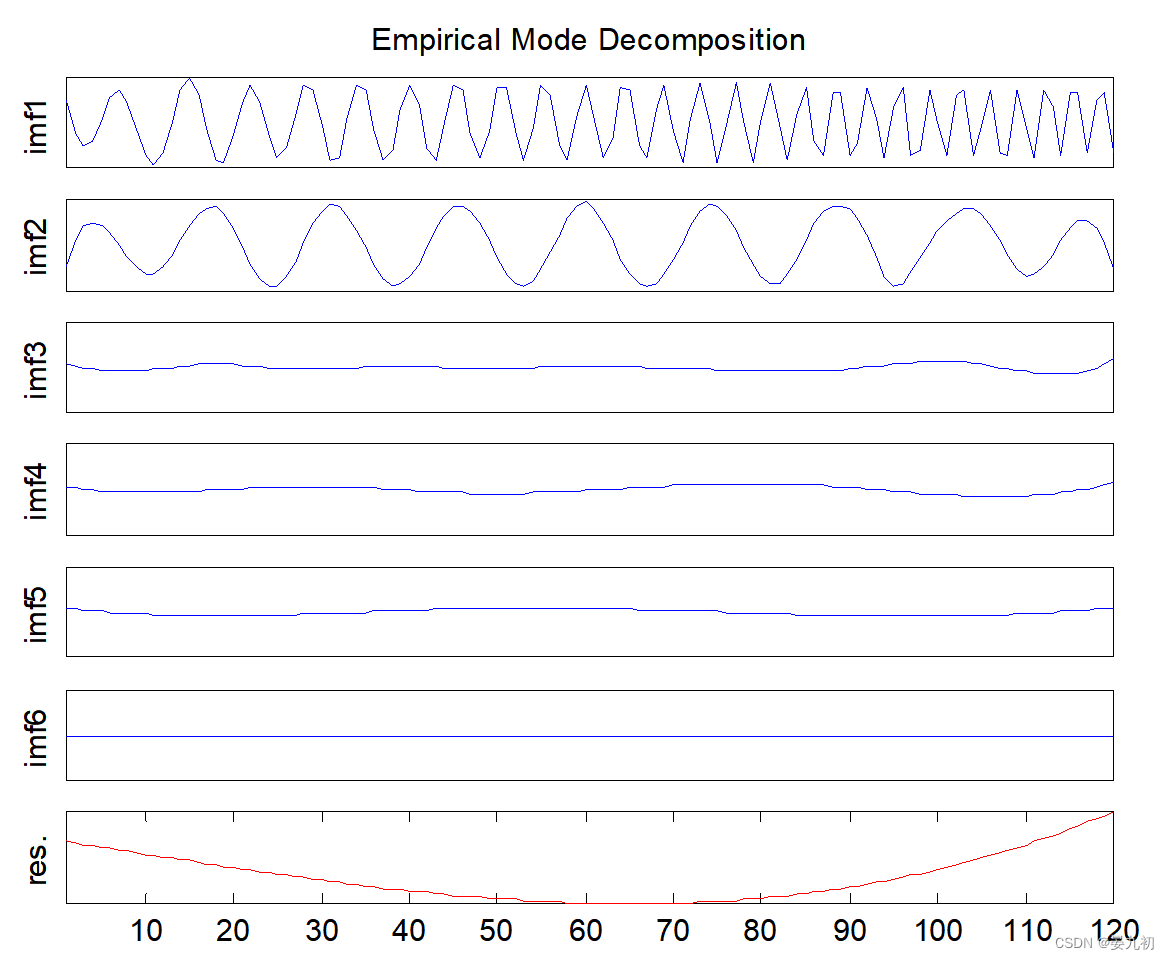
EMD方法适用信号范围广泛,无需设定基函数,克服了小波变换中基函数无自适应性的问题。但是利用EMD方法有两个缺陷:
1 . 模态混叠现象
用EMD分解得到的IMF存在模态混叠,有下列情况之一可以称为模态混叠:
①在同一个IMF分量中,存在尺度分布范围很宽却又各不相同的信号
②在不同的IMF分量中,存在着尺度相近的信号
2.端点效应
端点效应由两种情形造成的:
①在三次样条拟合中产生
②在Hilbert变换中产生,导致信号开始之前和结尾之后没有样本被考虑
EEMD(集合经验模态分解):
利用EMD滤波器组行为及白噪声频谱均匀分布的统计特性,使Sifting过程信号极值点分布更趋匀称,有效抑制由间歇性高频分量等因素造成的模态混叠。
EEMD方法的本质是一种叠加高斯白噪声的多次经验模态分解(EMD),利用了高斯白噪声具有频率均匀分布的统计特性,通过每次加入同等幅值的不同白噪声来改变信号的极值点特性,之后对多次EMD得到的相应IMF进行总体平均来抵消加入的白噪声,从而有效抑制模态混叠的产生。
CEEMD(互补集合经验模态分解):
向原始信号中加入正负成对的辅助白噪声,在集合平均时相消,能有效提高分解效率,克服EEMD重构误差大、分解完备性差的问题。
优点有:
- 集总平均次数会减少,从百量级减小到几十的量级。
- 重建后的信号噪声明显减少。
- 集总平均次数越多,噪声越小
但 CEEMD的不足之处在于进行EMD分解时产生的IMF个数仍存在差异,导致最终集合平均时IMF分量对齐困难,或导致集合平均产生误差。
CEEMDAN(自适应噪声完备集合经验模态分解):
在分解过程中添加的是白噪声经EMD分解得到的各阶IMF分量,最后重构信号中的噪声残余(比EEMD的结果)更小,降低了筛选次数。
另一方面,各组信号经CEEMDAN分解出第一阶固有模态分量后立即进行集合平均,避免了CEEMD中各组IMF分解结果差异造成最后集合平均难以对齐的问题,也避免了其中某一阶IMF分解效果不好时,将影响传递给下一阶,影响后续分解。
ESMD(极点对称模态分解):
将外部包络线插值改为内部极点对称插值
视频:https://www.zhihu.com/zvideo/1326624034449252352
方法介绍:https://zhuanlan.zhihu.com/p/334628925
对应论文:https://www.doc88.com/p-0788912839541.html
别人提出的改进策略:https://www.hanspub.org/journal/PaperInformation.aspx?paperID=27923
(改善每半个周期中关于中点不对称的数据的分解性能)
VMD(变分模态分解)
变分模态分解(VMD)是2014年提出的一种非递归信号处理方法,通过迭代搜索变分模态的最优解,变分问题,就是有关求泛函的极大值和极小值的问题,研究对象是函数,目的是求极值。
可将时间序列数据分解为一系列具有有限带宽的本征模态函数(IMF),可自适应更新各IMF的最优中心频率和带宽。
VMD具有较好抗噪能力,可以克服经验模态分解(EMD)频率混叠的问题。因为某个IMF频率如果合理,那它的频率应该比较集中在比较窄的一个范围,但实际上,EMD分解中,某一窄带的频率可能分布在不同IMF中。
LMD(局部均值分解):
1)LMD 的分解结果是一系列瞬时频率具有物理意义的PF 分量之和,PF 分量由包络信
号和纯调频信号相乘得到,从纯调频信号计算得到的瞬时频率是正的、连续的、具
有物理意义的。而EMD 方法是先得到 IMF 分量,然后对IMF 分量进行 Hilbert 变换
求得瞬时频率和瞬时幅值,则可能产生无法解释的负频率。
2)LMD 方法采用平滑处理的方法形成局部均值函数和局域包络函数,因此可以避免
EMD 方法中采用三次样条函数形成上下包络线时产生的过包络、欠包络现象。
(3) LMD 的端点效应相比较 EMD,在程度上轻得多,作用范围也比较小。这主要体现
在下面三个方面:
①LMD 信号端点附近未知包络线的长度比 EMD 的短。
②存在特殊的信号,经 LMD 的结果不受端点效应影响,如端点为极值的调幅调频信号。
③LMD 端点效应的扩散速度比 LMD 慢
RLMD(局部鲁棒均值分解)
局部均值分解算法能够根据信号自身的复杂程度及变化规律,将一个复杂的多分量信号通过多重循环迭代的方式,逐步分解成若干个乘积函数和一个残余分量之和,而每一个乘积函数都是一个包络函数和一个纯调频函数的乘积,理论上应与某一物理过程对应。
RLMD从3个方面对局部均值分解方法进行优化。
对边界条件的优化
对边界条件的优化采用镜像延拓法对信号进行延伸,能够减弱端点效应
对信号的包络估计的优化
在估计信号包络时采用移动平均算法,基于统计理论的统计方法选取适当的滑窗长度
筛分停止准则的优化
通过软筛分停止准则进行最优的筛分迭代次数的自适应寻找














