系列文章目录

第1章 专家系统

第2章 决策树

第3章 神经元和感知机

识别手写数字——感知机

第4章 线性回归

第5章 逻辑斯蒂回归和分类

第5章 支持向量机

第6章 人工神经网络(一)

第6章 人工神经网络(二) 卷积和池化

第6章 使用pytorch进行手写数字识别

实操练习 使用Yolo模型进行物体检测

第7章 集成学习 AdaBoost算法

文章目录

• 系列文章目录
• 前言
• 一、提升方法的基本思路
• 二、梯度提升算法
• • 回顾梯度下降法
  • 梯度提升算法
  • 均方误差的梯度提升算法
  • 三、偏差与方差
  • 总结

    ---

    前言

    自适应增强算法AdaBoost是一种提升(Boosting)算法。提升算法，或者叫作增强算法，是以迭代的方式将若干弱模型组合为一个强模型，每一轮迭代产生一个“弱模型”,经过若干轮迭代之后，将弱模型进行加权融合，组成一个“强模型”。这就是提升算法的一般框架。而梯度提升算法，是另一种应用广泛的通用提升算法。

    ---

    一、提升方法的基本思路

    提升方法基于这样一种思想：对于一个复杂任务来说，将多个专家的判断进行适当的总和所得出的判断，要比其中任何一个专家单独的判断好。

    “强可学习”strongly learnable

    在概率近似正确(probably approximately correct, PAC)学习的框架中，一个概念（一个类），如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的。

    “弱可学习”weakly learnable

    一个概念（一个类），如果存在一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么就称这个概念是弱可学习的。

    Schapire后来证明强可学习与弱可学习是等价的，也就是说，在PAC学习的框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。

    这样一来，如果已经发现了“弱学习算法”，那么能否将它提升(boost)为“强学习算法” 呢？

    对于分类问题而言，给定一个训练样本集，求比较粗糙的分类规则（弱学习器）要比求精确的分类规则（强分类器）容易得多。提升方法就是从弱学习算法出发，反复学习，得到一系列弱分类器（又称基本分类器），然后组合这些弱分类器，构成一个强分类器。

    大多数的提升方法都是改变训练数据的概率分布（训练数据的权值分布），针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。

    对于提升方法来说，有两个问题需要回答：一是在每一轮如何改变训练数据的权值或者概率分布；二是如何将弱分类器组合成一个强分类器。

    对于第一个问题，AdaBoost的做法是，提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。这样一来，那些没有得到正确分类的数据，由于其权值的加大，而受到后一轮的弱分类器的更大的关注。于是，分类问题被一系列的弱分类器“分而治之”。

    对于第二个问题，AdaBoost采取加权多数表决的方法，加大分类误差小的弱分类器的权值，使其在表决中起较大作用；减小分类误差大的弱分类器的权值，使其在表决中起较小的作用。

    二、梯度提升算法

    梯度提升算法(Gradient Boosting)是梯度下降法(Gradient Desent Method)和提升算法(Boosting Algorithm)的结合。该算法将回归问题看作某种损失函数的优化问题，这是应用“梯度下降法”的一般思路。

    回归问题的目标是产生一个函数映射,从给定的输入 x \boldsymbol{x} x产生一个输出 F ( x ) F(\boldsymbol{x}) F(x)。训练数据是一些已知的 ( x , y ) (\boldsymbol{x},y) (x,y)组合，训练这个预测模型的目标就是缩小 F ( x ) F(x) F(x)和 y y y的差距。可以采用最小二乘法中的均方误差，逻辑斯蒂回归中的交叉熵损失函数等。我们可以抽象的把这种差距记为函数 L ( F ( x ) , y ) L(F(\boldsymbol{x}),y) L(F(x),y) ,而梯度提升算法的目标就是最小化这个函数的值，这样我们就将一个回归问题转化为一个函数优化问题，对于函数优化问题，就可以采用梯度下降算法来解决。

    回顾梯度下降法

    梯度下降法的优化对象通常是模型的参数变量，而在梯度提升算法中，优化的对象是“弱模型”，弱模型本身就是一个函数，因此，我们要从“变量空间”的梯度下降，迁移到“函数空间”的梯度下降。

    我们先观察“变量空间”中的梯度下降。假设我们要计算使得 L ( x ) L(\boldsymbol{x}) L(x)取得极小值的 x ∗ \boldsymbol{x}^* x∗。

    x ∗ = a r g   m i n x   L ( x ) \boldsymbol{x}^*=arg \space \underset{x}{min} \space L(\boldsymbol{x}) x∗=arg xmin​ L(x)

    首先，给 x \boldsymbol{x} x一个初始猜测 x 0 \boldsymbol{x}_0 x0​。然后计算在 x = x 0 \boldsymbol{x=\boldsymbol{x}_0} x=x0​出的梯度，然后朝着梯度相反的方向给 x 0 \boldsymbol{x}_0 x0​一个增量 Δ x 1 \Delta \boldsymbol{x}_1 Δx1​，得到 x 1 \boldsymbol{x}_1 x1​，依次类推。

    在第 m m m次迭代，我们要计算如下的梯度 g m \boldsymbol{g}_m gm​：

    g m = { [ ∂ L ( x ) ∂ x ] x = x m − 1 } \boldsymbol{g}_{m}=\left\{\left[\frac{\partial L(\boldsymbol{x})}{\partial \boldsymbol{x}}\right]_{\boldsymbol{x}=\boldsymbol{x}_{m-1}}\right\} gm​={[∂x∂L(x)​]x=xm−1​​}

    其中 x m − 1 \boldsymbol{x}_{m-1} xm−1​是此前 m − 1 m-1 m−1次迭代的增量累加的结果。为了表达方便，我们令 Δ x 0 = x 0 \Delta \boldsymbol{x}_0=\boldsymbol{x}_0 Δx0​=x0​，则有

    x m − 1 = ∑ i = 0 m − 1 Δ x i \boldsymbol{x}_{m-1}=\sum_{i=0}^{m-1}{\Delta \boldsymbol x_i} xm−1​=i=0∑m−1​Δxi​

    每次迭代的增量都朝着梯度相反的方向。设第 m m m次的学习率为 ρ m \rho_m ρm​，那么，第 m m m次的增量 Δ x m \Delta \boldsymbol x_m Δxm​如下：

    Δ x m = − ρ m g m \Delta \boldsymbol x_m = -\rho _m \boldsymbol{g}_{m} Δxm​=−ρm​gm​

    这个学习率也是可以优化的，根据损失函数找到每一步的最佳学习率。这相当于在梯度相反的方向上做一次线性搜索，找到使得损失函数极小化的点。

    ρ m = a r g   m i n ρ   L ( x m − 1 − ρ g m ) \rho_m=arg \space \underset{\rho}{min} \space L(\boldsymbol{x}_{m-1}-\rho \boldsymbol{g}_m) ρm​=arg ρmin​ L(xm−1​−ρgm​)

    以上就是对梯度下降法的一般性描述。最终经过 M M M次迭代，可以找到一个能够极小化 L ( x ) L(\boldsymbol{x}) L(x)的 x M \boldsymbol{x}_M xM​，这个 x M \boldsymbol{x}_M xM​实际上是若干个增量 Δ x m \Delta \boldsymbol{x}_m Δxm​的线性和，也就是若干个负梯度 − g m -\boldsymbol{g}_m −gm​的加权线性和。

    梯度提升算法

    下面我们将变量 x \boldsymbol{x} x换成函数 F F F，也就是预测模型最终希望得到的“强模型” 这个强模型最终是若干个“弱模型”的加权融合，产生弱模型的弱学习器的学习目标，是在每一轮迭代中向损失函数 L L L的梯度相反的方向前进一点。

    我们要把梯度下降法中的变量 x \boldsymbol{x} x换成函数 F ( x ) F(\boldsymbol{x}) F(x)。假设训练数据集是一个有限的集合 ( x 1 , y 1 ) , ⋯   , ( x N , y N ) (\boldsymbol{x}_1,y_1),\cdots,(\boldsymbol{x}_N,y_N) (x1​,y1​),⋯,(xN​,yN​)，一共包含了 N N N组输入/输出组合 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi​,yi​)。我们的优化目标随之变为，寻找一个最优的函数 F ∗ ( x ) F^*(\boldsymbol{x}) F∗(x)使得损失函数 L L L最小化。

    F ∗ = a r g   m i n F   ∑ i = 1 N L ( F ( x i ) , y i ) F^*=arg \space \underset{F}{min} \space \sum_{i=1}^{N} L(F(\boldsymbol{x}_i),y_i) F∗=arg Fmin​ i=1∑N​L(F(xi​),yi​)

    从一个简单的预测模型开始，假设这个模型的预测值是一个常数。如果误差函数 L L L是均方误差，那么，这个预测值实际上就是训练集中 y i y_i yi​的平均值。对于任意误差函数 L L L，我们可以用下面更加一般化的形式描述这个初始模型的“粗糙”猜测 F 0 F_0 F0​。

    F 0 ( x ) = a r g   m i n ρ   ∑ i = 1 N L ( ρ , y i ) F_0(\boldsymbol{x})=arg \space \underset{\rho}{min} \space \sum_{i=1}^{N} L(\rho,y_i) F0​(x)=arg ρmin​ i=1∑N​L(ρ,yi​)

    然后开始迭代，从 F 0 F_0 F0​得到 F 1 F_1 F1​，进而得到 F 2 F_2 F2​，依次类推，最终逼近 F ∗ F^* F∗。

    假设已经有了 F m − 1 F_{m-1} Fm−1​，现在是第 m m m次迭代。计算误差函数 L L L相对于预测模型输出的 F ( x ) F(\boldsymbol{x}) F(x)的偏导数，在每一个数据点 x i \boldsymbol{x}_i xi​上计算偏导数的相反数，把这个结果记作 y ~ i \tilde{y}_i y~​i​。

    y ~ i = − [ ∂ L ( F ( x i ) , y i ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) \tilde {y}_i =- \left [ \frac{\partial L(F(\boldsymbol{x}_i),y_i)}{\partial F(\boldsymbol{x}_i)} \right ] _{F(\boldsymbol{x})=F_{m-1}(\boldsymbol{x})} y~​i​=−[∂F(xi​)∂L(F(xi​),yi​)​]F(x)=Fm−1​(x)​

    这样，会得到 N N N组 ( x i , y ~ i ) (\boldsymbol{x}_i,\tilde y_i) (xi​,y~​i​)，它们构成了一个新的数据集。这个新的数据集是由误差函数的负梯度组成的，它代表了 F F F的改进方向。我们要用一个弱学习器去学习如何改进。假设弱学习器是一个函数族 h ( x ; a ) h(\boldsymbol{x};\boldsymbol{a}) h(x;a)，其中 a \boldsymbol{a} a是函数的参数，也就是弱学习器要学习的参数。

    现在，要在数据集 { ( x i , y ~ ) } i = 1 N \left \{(\boldsymbol{x}_i,\tilde{y}) \right\}_{i=1}^{N} {(xi​,y~​)}i=1N​上用弱学习器得到一个参数为 a m \boldsymbol{a}_m am​的若预测模型 h ( x ; a m ) h(\boldsymbol{x};\boldsymbol{a}_m) h(x;am​)，它将是最终得到的强模型的一部分。

    接下来，要决定这一轮得到的弱模型 h ( x ; a m ) h(\boldsymbol{x};\boldsymbol{a}_m) h(x;am​) 在最终的模型中所占据的比例 ρ m \rho_m ρm​。这仍然是一个最优化问题，优化的目标依然是误差函数 L L L。

    ρ m = a r g   m i n ρ   ∑ i = 1 N L ( F m − 1 ( x i ) + ρ h ( x i ; a m ) ,   y i ) \rho_m=arg \space \underset{\rho}{min} \space \sum_{i=1}^{N} L(F_{m-1}(\boldsymbol{x}_i)+\rho h(\boldsymbol{x}_i;\boldsymbol{a}_m) , \space y_i) ρm​=arg ρmin​ i=1∑N​L(Fm−1​(xi​)+ρh(xi​;am​), yi​)

    然后，就得到了改进后的 F m F_m Fm​，可以开始下一轮迭代，或者达到终止条件而结束迭代过程。

    F m ( x ) = F m − 1 ( x ) + ρ m h ( x ; a m ) F_m(\boldsymbol{x})=F_{m-1}(\boldsymbol{x})+\rho_mh(\boldsymbol{x};\boldsymbol{a}_m) Fm​(x)=Fm−1​(x)+ρm​h(x;am​)

    这就是一般化的梯度提升算法。

    算法2：梯度提升算法

    建立初始模型 F 0 ( x ) = a r g   m i n ρ ∑ i = 1 N L ( ρ , y i ) F_0(\boldsymbol{x})=arg \space \underset{\rho}{min} \sum_{i=1}^{N}L(\rho,y_i) F0​(x)=arg ρmin​∑i=1N​L(ρ,yi​)

    for m = 1 , 2 , ⋯   , M m=1,2,\cdots,M m=1,2,⋯,M do

    对所有样本 i = 1 , ⋯   , N , i=1,\cdots,N, i=1,⋯,N,计算梯度 y ~ i = − [ ∂ L ( F ( x i ) , y i ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) \tilde{y}_i=-\left [ \frac{\partial L(F(\boldsymbol{x}_i),y_i)}{\partial F(\boldsymbol{x}_i)} \right ] _{F(\boldsymbol{x})=F_{m-1}(\boldsymbol{x})} y~​i​=−[∂F(xi​)∂L(F(xi​),yi​)​]F(x)=Fm−1​(x)​

    在数据集 { ( x i , y ~ ) } i = 1 N \left \{(\boldsymbol{x}_i,\tilde{y}) \right\}_{i=1}^{N} {(xi​,y~​)}i=1N​上，用弱学习器得到模型 h ( x ; a m ) h(\boldsymbol{x};\boldsymbol{a}_m) h(x;am​)

    计算弱模型的最优权重 ρ m = a r g   m i n ρ   ∑ i = 1 N L ( F m − 1 ( x i ) + ρ h ( x i ; a m ) ,   y i ) \rho_m=arg \space \underset{\rho}{min} \space \sum_{i=1}^{N} L(F_{m-1}(\boldsymbol{x}_i)+\rho h(\boldsymbol{x}_i;\boldsymbol{a}_m) , \space y_i) ρm​=arg ρmin​ ∑i=1N​L(Fm−1​(xi​)+ρh(xi​;am​), yi​)

    得到改进后的模型 F m ( x ) = F m − 1 ( x ) + ρ m h ( x ; a m ) F_m(\boldsymbol{x})=F_{m-1}(\boldsymbol{x})+\rho_mh(\boldsymbol{x};\boldsymbol{a}_m) Fm​(x)=Fm−1​(x)+ρm​h(x;am​)

    end

    均方误差的梯度提升算法

    接下来我们将误差函数 L L L替换为一些真实的误差后，更加直观理解梯度提升算法的意义。

    我们使用均方误差 L ( F , y ) = ( F − y ) 2 / 2 L(F,y)=(F-y)^2/2 L(F,y)=(F−y)2/2，均方误差的梯度计算如下，我们需要梯度的反方向(梯度下降)，所以这里取偏导数的相反数。

    − ∂ L ∂ F = y − F -\frac{\partial L}{\partial F} = y-F −∂F∂L​=y−F

    值得注意的是，当我们采用均方误差时，初始模型输出的常数值是所有样本 y i y_i yi​的平均值。

    y ˉ = 1 N ∑ i = 1 N y i = a r g   m i n ρ ∑ i = 1 N ( y i − ρ ) 2 \bar{y} =\frac{1}{N} \sum_{i=1}^{N} y_i = arg \space \underset{\rho}{min} \sum_{i=1}^{N}{(y_i-\rho)}^2 yˉ​=N1​i=1∑N​yi​=arg ρmin​i=1∑N​(yi​−ρ)2

    均方误差与绝对误差 L ( F − y ) = ∣ F − y ∣ L(F-y)=|F-y| L(F−y)=∣F−y∣比较：

    绝对误差的最优常数输出是 y i y_i yi​的中位数。

    中位数与平均值的差别就在于其对噪声（离群点）的敏感度。离大多数值较远的噪声点会把平均值拉向噪声的方向，而对中位数没有影响。

    现在将均方误差代入一般化的梯度提升算法。

    算法3：采用均方误差的梯度提升算法

    建立初始模型 F 0 ( x ) = y ˉ F_0(\boldsymbol{x})=\bar y F0​(x)=yˉ​

    for m = 1 , 2 , ⋯   , M m=1,2,\cdots,M m=1,2,⋯,M do

    对所有样本 i = 1 , ⋯   , N , i=1,\cdots,N, i=1,⋯,N,计算残差 y ~ i = y i − F m − 1 ( x i ) \tilde{y}_i=y_i-F_{m-1}(\boldsymbol{x}_i) y~​i​=yi​−Fm−1​(xi​)

    在数据集 { ( x i , y ~ ) } i = 1 N \left \{(\boldsymbol{x}_i,\tilde{y}) \right\}_{i=1}^{N} {(xi​,y~​)}i=1N​上，用弱学习器得到模型 h ( x ; a m ) h(\boldsymbol{x};\boldsymbol{a}_m) h(x;am​)

    计算弱模型的最优权重 ρ m = a r g   m i n ρ   ∑ i = 1 N L ( F m − 1 ( x i ) + ρ h ( x i ; a m ) ,   y i ) \rho_m=arg \space \underset{\rho}{min} \space \sum_{i=1}^{N} L(F_{m-1}(\boldsymbol{x}_i)+\rho h(\boldsymbol{x}_i;\boldsymbol{a}_m) , \space y_i) ρm​=arg ρmin​ ∑i=1N​L(Fm−1​(xi​)+ρh(xi​;am​), yi​)

    得到改进后的模型 F m ( x ) = F m − 1 ( x ) + ρ m h ( x ; a m ) F_m(\boldsymbol{x})=F_{m-1}(\boldsymbol{x})+\rho_mh(\boldsymbol{x};\boldsymbol{a}_m) Fm​(x)=Fm−1​(x)+ρm​h(x;am​)

    end

    均方误差的梯度恰好是模型输出与真实目标输出之间的“残差”，实际上，我们是在教弱学习器从残差中学习，用这种方式不断逼近真实的目标输出。

    三、偏差与方差

    对于算法模型，我们希望能够衡量它在未知样本上的预测误差。

    假设我们希望预测的问题是一个函数关系 y = f ( x ) y=f(x) y=f(x)， x x x是输入， y y y是输出。

    我们有一些训练样本 D D D，然后通过某个算法我们可以训练得到模型 f ^ D \hat{f}_D f^​D​，它在某个未知样本 x x x上的误差是 ( y − f ^ D ) 2 (y-\hat{f}_D)^2 (y−f^​D​)2。由于训练样本总是只能覆盖样本空间中极其有限的样本，而且采集训练样本的过程中难免有一些误差（噪声或观测误差，比如标记错误的样本，模糊不清的图片等），因此，训练得到的模型总会不可避免地存在误差。

    采用不同地训练样本集 D D D，就会有不同的误差。衡量算法的效能应该是与 D D D无关的，因此，我们用误差对所有可能的 D D D的期望来衡量算法的预测误差，即采用不同训练集得到的不同模型的平均误差。

    模型误差的期望可以分解为偏差Bias的平方、方差Variance和随机噪声( σ 2 \sigma^2 σ2)的和。

    即

    E D [ ( y − f ^ D ( x ) 2 ) ] = ( B i a s D ) 2 + V a r D + σ 2 E_D [(y-\hat{f}_D(x)^2)]=(Bias_D)^2+Var_D+\sigma^2 ED​[(y−f^​D​(x)2)]=(BiasD​)2+VarD​+σ2

    其中，偏差是不同训练集得到的不同模型的预测结果的均值与样本的真实值之间的差异。

    B i a s D = E D [ f ^ D ( x ) ] − f ( x ) Bias_D=E_D[\hat{f}_D(x)]-f(x) BiasD​=ED​[f^​D​(x)]−f(x)

    方差是不同模型对于同一未知样本的预测值的方差。

    V a r D = E D [ ( E D [ f ^ D ( x ) ] − f ^ D ( x ) ) 2 ] Var_D=E_D \left [(E_D[\hat{f}_D(x)]-\hat{f}_D(x))^2 \right ] VarD​=ED​[(ED​[f^​D​(x)]−f^​D​(x))2]

    当模型的偏差比较大时，通常表示模型没有足够的表达力。无论采取怎样的训练样本进行训练，都不能使得模型拟合样本数据，模型的预测值与真实值有较大的差距，即欠拟合。

    当模型的方差比较大时，模型的表达力足够强，能很好地拟合所有训练样本，但是在未知样本上地预测非常不稳定，这种情况叫作欠拟合。这说明模型包含了超出真实问题地复杂度，过多的参数无法从有限的样本中获取充分的信息，这些参数就会自由摆动，从而扰动模型的预测结果，使模型表现得不稳定。

    

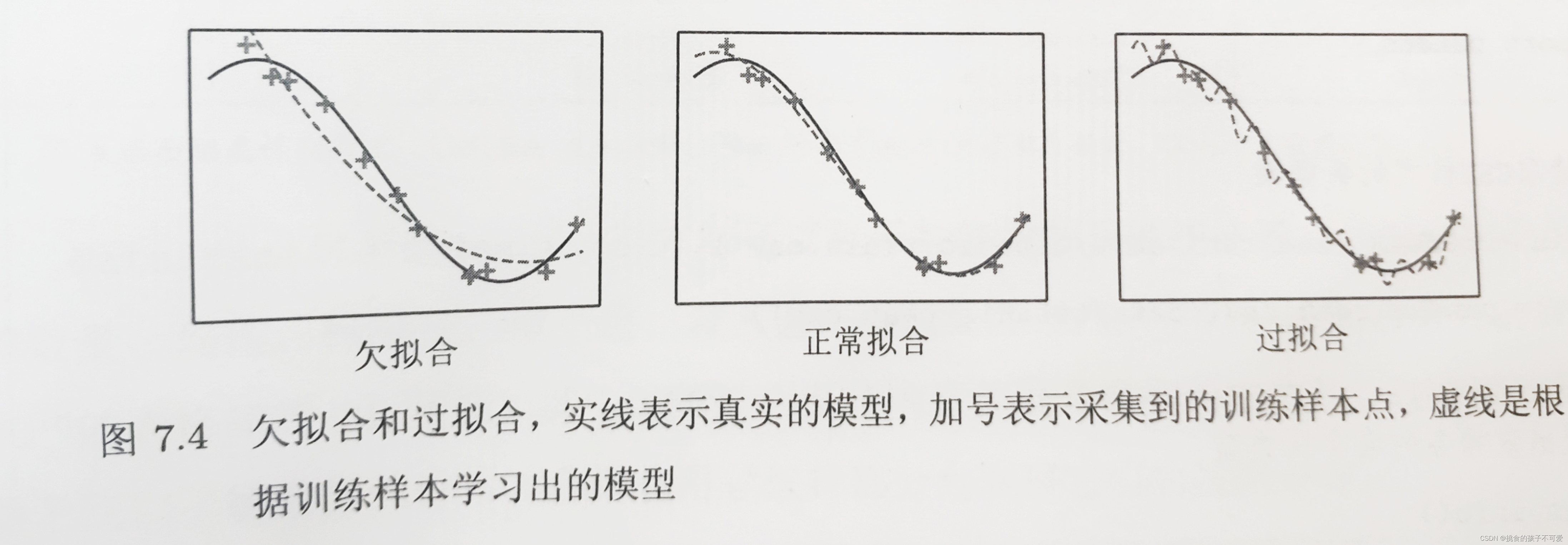
    不同的集成学习方法分别从偏差和方差的角度降低模型的预测误差。

    随机森林这类方法将若干方差较大的模型进行平均，降低了模型的方差。

    而AdaBoost这样的方法将若干偏差大、方差小的模型进行加权叠加，以增加模型的表达力，减小模型的偏差。

    ---

    总结

    今天从梯度下降法开始，学习了梯度提升算法的实现，了解了它的数学一般表示形式。在梯度 下降法的基础上，运用迭代的思想，将不同的模型进行组合，就得到了梯度提升算法。

     
     网站设计模板  十大免费ppt网站  深圳网页制作服务商  创意网站建设设计公司  如何建站  html代码