MK趋势检验

在时间序列趋势分析中，Mann-Kendall检验是世界气象组织推荐并已被广泛使用的非参数检验方法，最初由Mann和Kendall提出，现已被很多学者用来分析降雨、气温、径流和水质等要素时间序列的趋势变化。Mann-Kendall检验不需要样本遵从一定的分布，也不受少数异常值的干扰，适用于水文、气象等非正态分布的数据，计算简便。

代码如下：

这是代码1

% Mann-Kendall趋势检测 
% Time Series Trend Detection Tests
% [ z, sl, lcl, ucl ] = trend( y, dt )
% where z = Mann-Kendall Statistic
% sl = Sen's Slope Estimate
% lcl = Lower Confidence Limit of sl
% ucl = Upper Confidence Limit of sl
% y = Time Series of Data
% dt = Time Interval of Data
% nor给定的显著性水平 当Z的绝对值大于等于1.64、 1.96、 2.58时则说明该时间序列分别通过了置信水平90%、95%、99%的显著性检验
%y是待检测数据序列
function [ z, sl, lcl, ucl ] = mk( y )
n = length( y );
dt=1;
% Mann-Kendall Test for N > 40
    % disp( 'Mann-Kendall Test;' );
    % if n < 41,
    % disp( 'WARNING - sould be more than 40 points' );
    % end;
% calculate statistic
s = 0;
for k = 1:n-1
    for j = k+1:n
        s = s + sign( y(j) - y(k) );
    end
end
% variance ( assuming no tied groups )
v = ( n * ( n - 1 ) * ( 2 * n + 5 ) ) / 18;
% test statistic
if s == 0
z = 0;
elseif s > 0
z = ( s - 1 ) / sqrt( v );
else
z = ( s + 1 ) / sqrt( v );
end
% should calculate Normal value here
nor = 1.96;%当Z的绝对值大于等于1.64、 1.96、 2.58时则说明该时间序列分别通过了置信水平90%、95%、99%的显著性检验
% results
disp( [ ' n = ' num2str( n ) ] );
disp( [ ' Mean Value = ' num2str( mean( y ) ) ] );
disp( [ ' Z statistic = ' num2str( z ) ] );
if abs( z ) < nor
    disp( ' No significant trend' );
    z = 0;
elseif z > 0
    disp( ' Upward trend detected' );
else
    disp( ' Downward trend detected' );
end
    disp( 'Sens Nonparametric Estimator:' );
% calculate slopes
ndash = n * ( n - 1 ) / 2;
s = zeros( ndash, 1 );
i = 1;
for k = 1:n-1
    for j = k+1:n
    s(i) = ( y(j) - y(k) ) / ( j - k ) / dt;
    i = i + 1;
    end
end
% the estimate
sl = median( s );%M = median(A) 返回 A 的中位数值。
disp( [ ' Slope Estimate = ' num2str( sl ) ] );
% variance ( assuming no tied groups )
v = ( n * ( n - 1 ) * ( 2 * n + 5 ) ) / 18;
m1 = fix( ( ndash - nor * sqrt( v ) ) / 2 );
m2 = fix( ( ndash + nor * sqrt( v ) ) / 2 );
s = sort( s );
lcl = s( m1 );
ucl = s( m2 + 1 );
disp( [ ' Lower Confidence Limit = ' ...
num2str( lcl ) ] );
disp( [ ' Upper Confidence Limit = ' ...
num2str( ucl ) ] );

对于**标准值Z（Z statistic），其大于0，则序列呈上升趋势；若其小于0，则序列呈下降趋势。**当Z的绝对值大于等于1.64、 1.96、 2.58时则说明该时间序列分别通过了置信水平90%、95%、99%的显著性检验

斜率（Slope Estimate）用于衡量趋势大小，当斜率大于0 反应上升趋势，反之亦然。

还有代码2（计算结果一致，制图结果不一样）：

function  [Zs ,beta ,UFk ,UBk2 ]= MKtrend2(Data,n)
% MKTest函数用于趋势和突变检验
% 输入参数
% Data    序列数据
% n         序列长度
% 输出参数
% Zs       统计量
% beta    斜率
% UFk     统计量UFk
% UBk2   逆序统计量
%% 趋势分析线性:Mann-Kendall检验
Sgn=zeros(n-1,n-1);        %初始化分配内存
for i=1:n-1
    for j=i+1:n
        if((Data(j)-Data(i))>0)
            Sgn(i,j)=1;
        else
            if((Data(j)-Data(i))==0)
                Sgn(i,j)=0;
            else
                if((Data(j)-Data(i))<0)
                    Sgn(i,j)=-1;
                end
            end
        end
    end
end
Smk=sum(sum(Sgn));
VarS=n*(n-1)*(2*n+5)/18;
if n>10
    if Smk>0
        Zs=(Smk-1)/sqrt(VarS);
    else
        if Smk==0
            Zs=0;
        else
            if  Smk<0
                Zs=(Smk+1)/sqrt(VarS);
            end
        end
    end
end
%% beta 斜率 描述单调趋势
t=1;
for i=2:n
   for j=1:(i-1)
       temp(t)=( Data(i)-Data(j) )/( i-j );
       t=t+1;
   end
end
beta=median( temp );
%% 突变检验
Sk=zeros(n,1);          % 定义累计量序列Sk
UFk=zeros(n,1);        % 定义统计量UFk
s = 0;
% 正序列计算start---------------------------------
for i=2:n
   for j=1:i
         if Data(i)>Data(j)
           s=s+1;
         else
           s=s+0;
         end
   end
   Sk(i)=s;
   E=i*(i-1)/4; % Sk(i)的均值
  Var=i*(i-1)*(2*i+5)/72; % Sk(i)的方差
  UFk(i)=(Sk(i)-E)/sqrt(Var);
end
% 正序列计算end---------------------------------
% 逆序列计算start---------------------------------
Sk2=zeros(n);  % 定义逆序累计量序列Sk2
UBk=zeros(n,1); 
s=0;
Data2=flipud(Data);        % 按时间序列逆转样本y
for i=2:n
   for j=1:i
         if Data2(i)>Data2(j)
           s=s+1;
         else
           s=s+0;
         end
   end
   Sk2(i)=s;
   E=i*(i-1)/4; 
  Var=i*(i-1)*(2*i+5)/72; 
  UBk(i,1)=0-(Sk2(i)-E)/sqrt(Var);
end
% 逆序列计算end------------------------------
UBk2=flipud(UBk);
UFk=UFk';
UBk2=UBk2';
%{
figure(3)%画图
plot(1:n,UFk,'r-','linewidth',1.5);
hold on
plot(1:n,UBk2,'b-.','linewidth',1.5);
plot(1:n,1.96*ones(n,1),':','linewidth',1);
% axis([1,n,-5,8]);
legend('UF统计量','UB统计量','0.05显著水平');
xlabel('t (year)','FontName','TimesNewRoman','FontSize',12);
ylabel('统计量','FontName','TimesNewRoman','Fontsize',12);
%grid on
hold on
plot(1:n,0*ones(n,1),'-.','linewidth',1);
plot(1:n,1.96*ones(n,1),':','linewidth',1);
plot(1:n,-1.96*ones(n,1),':','linewidth',1);
%}
end

MK突变检验

MK突变趋势检验可以寻找到时间序列的突变发生点。

代码：

clc
clear all
% A=xlsread('C:\Users\DI cOS\Desktop\tt.xlsx','Sheet1','A2:B22');
load('D:\00.研究生学习\08.EEMD\eemd_TOT_40_all.mat');
B=allresidual(1732,:);
A=B';
% x=A(:,1); % 时间列
aaa=1981:1:2020;
x=aaa'; % 时间列
% y=A(:,2); % 数据列
y=A; % 数据列
N=length(y);
n=length(y);
Sk=zeros(size(y));
UFk=zeros(size(y));
s=0;
for i=2:n
   for j=1:i
         if y(i)>y(j)
           s=s+1;
         else
           s=s+0;
         end
   end
   Sk(i)=s;
   E=i*(i-1)/4; 
  Var=i*(i-1)*(2*i+5)/72; 
  UFk(i)=(Sk(i)-E)/sqrt(Var);
end
y2=zeros(size(y));
Sk2=zeros(size(y));
UBk=zeros(size(y));
s=0;
for i=1:n
    y2(i)=y(n-i+1);
end
for i=2:n
   for j=1:i
         if y2(i)>y2(j)
           s=s+1;
         else
           s=s+0;
         end
   end
   Sk2(i)=s;
   E=i*(i-1)/4; 
  Var=i*(i-1)*(2*i+5)/72;
  UBk(i)=0-(Sk2(i)-E)/sqrt(Var);
end
UBk2=zeros(size(y));
for i=1:n
   UBk2(i)=UBk(n-i+1);
end
h1=plot(x,UFk,'r-','linewidth',1.5);
hold on
h2=plot(x,UBk2,'b-.','linewidth',1.5);
axis([min(x),max(x),-5,6]);
xlabel('年份','FontName','TimesNewRoman','FontSize',12);
ylabel('时间序列数据','FontName','TimesNewRoman','Fontsize',12);
hold on
plot(x,0*ones(N,1),'-.','linewidth',1); 
ylim([-3 7]);
h3=plot(x,2.58*ones(N,1),':','linewidth',1);
plot(x,-2.58*ones(N,1),':','linewidth',1);
legend([h1 h2 h3],'UF统计量','UB统计量','0.01显著水平','Location','NorthEast');
f1=UFk;
f2=UBk2;

如何解读结果，如何判断突变点？

得到的结果如下：

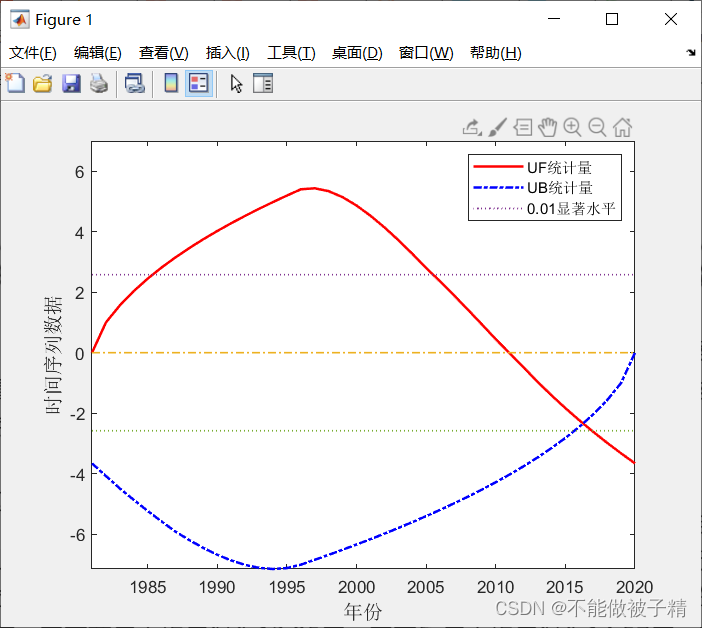
检验曲线图中若UF线在临界线内（两条显著性检验线之间，置信区间内）变动，表明变化曲线趋势和突变不明显;UF的值大于零，表明序列呈上升趋势，反之呈下降趋势;当其超过临界线时表明上升或下降趋势显著。如果UF和UB 2条曲线在临界线之间出现交点，则交点对应的时刻即为突变开始的时间;若交点出现在临界线外或出现多个交点，可结合其他检验方法进-步判定是否为突变点。

解读：

在1981-1987年间，数据呈不显著上升趋势，在1988-2005年间，数据呈显著上升趋势，在2006-2011年间数据呈不显著上升趋势，2012-2016年间，数据呈不显著下降趋势，在2017-2020年间，数据呈显著下降趋势。

可以看到UF曲线与UB曲线在置信区间上有个交点，为突变点，即在2017年左右开始发生突变。

参考文献：

[1]赵嘉阳. 中国1960-2013年气候变化时空特征、突变及未来趋势分析[D].福建农林大学,2017.