索取营销诊断书
021-80394720QQ
    您的位置：上海毫米网络优化公司 > 网站优化分享 >
    相关推荐recommended
    【数据结构】栈和队列超详解！(Stack && Queue)
    作者：mmseoamin日期：2024-03-04

    文章目录

    • 前言
    • 一、栈
      • 1、栈的基本概念
      • 2、栈的实现（数组实现）
      • 3、栈的基本操作
        • 3.1 栈的结构设计
        • 3.2 栈常见的基本函数接口
        • 4、栈的实现
          • 4.1 初始化栈
          • 4.2 栈的销毁
          • 4.3 入栈
          • 4.4 出栈
          • 4.5 判空
          • 4.6 长度
          • 4.7 获取栈顶元素
          • 完整代码
              • Stack.h
              • Stack.c
              • Test.c
              • 二、队列
                • 1、队列的结构及概念
                • 2、队列的实现（单链表实现）
                  • 1、队列的链式结构设计
                  • 2、常用的功能接口
                    • 2.1、初始化队列
                    • 2.2、销毁队列
                    • 2.3、入队列
                    • 2.4、出队列
                    • 2.5、获取队列头部元素
                    • 2.6、获取队列尾部元素
                    • 2.7、判空
                    • 2.8、获取有效元素个数
                    • 完整代码
                      • Queue.h
                      • Queue.c
                      • Test.c

                        前言

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第1张

                        一、栈

                        1、栈的基本概念

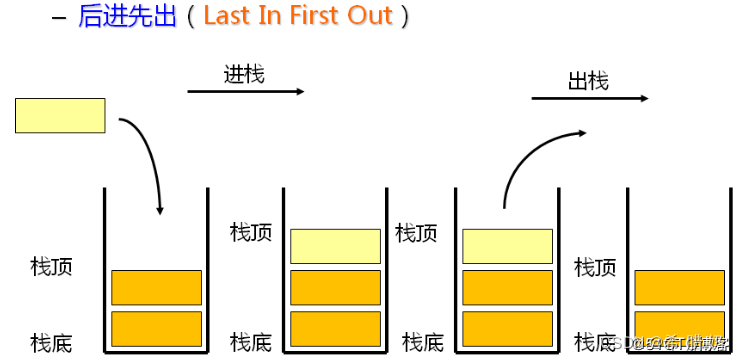
                        栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则

                        压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

                        出栈：栈的删除操作叫做出栈。出数据也在栈顶

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第2张

                        2、栈的实现（数组实现）

                        栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第3张

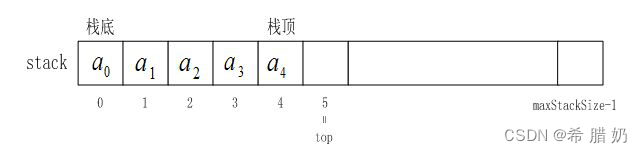
                        3、栈的基本操作

                        压栈：栈的插入操作，也叫进栈/入栈/压栈，在栈顶进行数据操作。

                        出栈：栈的删除操作，也是在栈顶进行数据删除的。

                        3.1 栈的结构设计

                        typedef int STDataType;//方便修改类型
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

                        3.2 栈常见的基本函数接口

                        //初始化
void STInit(ST* pst);
//销毁栈
void STDestroy(ST* pst);
//入栈
void STPush(ST* pst, STDataType x);
//出栈
void STPop(ST* pst);
//判空
bool STEmpty(ST* pst);
//长度
int STSize(ST* pst);
//栈顶
STDataType STTop(ST* pst);

                        4、栈的实现

                        4.1 初始化栈

                        //初始化
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = 0;//指向栈顶下一个元素,若等于-1则指向栈顶元素，两种任选
	pst->capacity = 0;
}

                        4.2 栈的销毁

                        //销毁栈
void STDestroy(ST* pst)
{
	assert(pst);
	tree(pst->a);
	pst->a = NULL;
	pst->top = 0;
	pst->capacity = 0;
}

                        4.3 入栈

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第4张

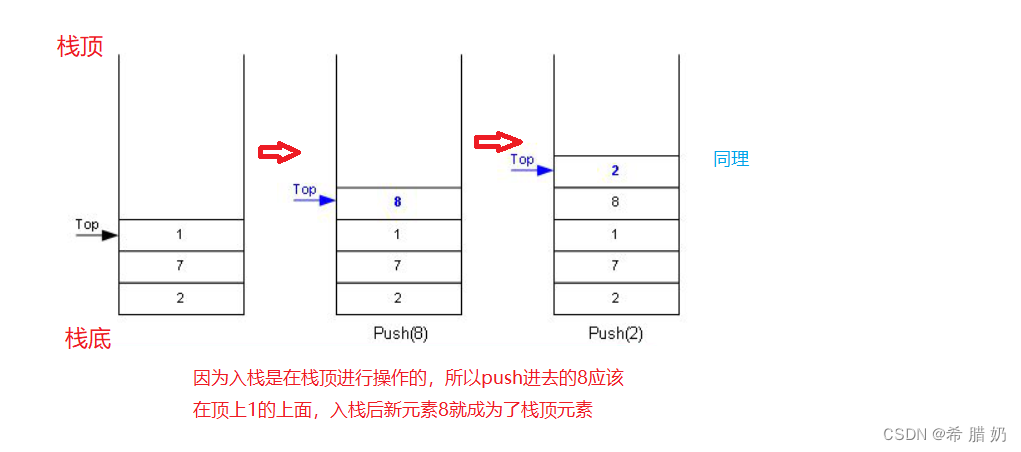
                        代码：

                        void STPush(ST* pst, STDataType x)
{
	assert(pst);
	//判断栈是否已满，满了就扩容
	if (pst->top == pst->capacity)
	{
		//使用三目运算符进行第一次开辟空间和后续扩容空间
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);
		//判断realloc是否开辟成功
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		//赋新值
		pst->a = tmp;
		pst->capacity = newcapacity;
	}
	//插入
	pst->a[pst->top] = x;
	pst->top++;
}

                        4.4 出栈

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第5张

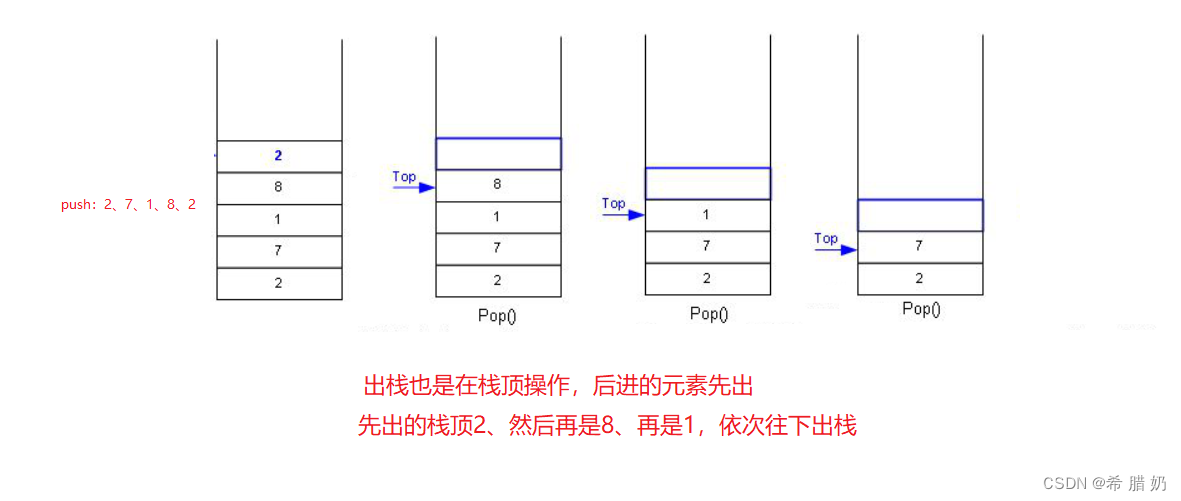
                        代码：

                        //出栈
void STPop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	pst->top--;
}

                        4.5 判空

                        //判空
bool STEmpty(ST* pst)
{
	assert(pst);  
	//返回值为0为假，非零为真
	return pst->top == 0;
}

                        4.6 长度

                        //长度
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

                        4.7 获取栈顶元素

                        注意：若栈顶指针初始化为pst->top = 0，即栈顶指针指向栈顶元素的下一个位置，则入栈操作变为pst->a[pst->top++]，出栈操作为pst->a[- -pst->top]。因为栈顶指针若初始化为 0 时，则栈顶指针始终指向顺序栈将要入栈的位置，也就是栈顶指针的下标就是入栈元素的下标。

                        //栈顶
STDataType STTop(ST* pst)
{
	assert(pst);
	return pst->a[pst->top - 1];
}

                        完整代码

                        Stack.h

                        #include
#include
#include
#include
typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;
//初始化
void STInit(ST* pst);
//销毁栈
void STDestroy(ST* pst);
//入栈
void STPush(ST* pst, STDataType x);
//出栈
void STPop(ST* pst);
//判空
bool STEmpty(ST* pst);
//长度
int STSize(ST* pst);
//栈顶
STDataType STTop(ST* pst);

                        Stack.c

                        #include"Stack.h"
//初始化
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = 0;//指向栈顶下一个元素
	pst->capacity = 0;
}
//销毁栈
void STDestroy(ST* pst)
{
	assert(pst);
	tree(pst->a);
	pst->a = NULL;
	pst->top = 0;
	pst->capacity = 0;
}
//入栈
void STPush(ST* pst, STDataType x)
{
	assert(pst);
	if (pst->top == pst->capacity)
	{
		int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		pst->capacity = newcapacity;
		pst->a = tmp;
	}
	pst->a[pst->top] = x;
	pst->top++;	
}
//出栈
void STPop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	pst->top--;
}
//判空
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}
//长度
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}
//栈顶
STDataType STTop(ST* pst)
{
	assert(pst);
	return pst->a[pst->top - 1];
}

                        Test.c

                        #include"Stack.h"
int main()
{
	ST st;
	//初始化
	STInit(&st);
	//插入+删除
	STPush(&st, 1);
	STPush(&st, 2);
	STPush(&st, 3);
	STPush(&st, 4);
	STPush(&st, 5);
	STPop(&st);
	STPop(&st);
	//长度
	STSize(&st);
	//栈顶
	STTop(&st);
	//销毁
	STDestroy(&st);
	return 0;
}

                        二、队列

                        1、队列的结构及概念

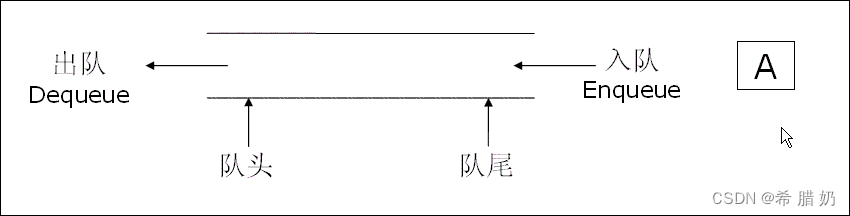
                        队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第6张

                        2、队列的实现（单链表实现）

                        队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第7张

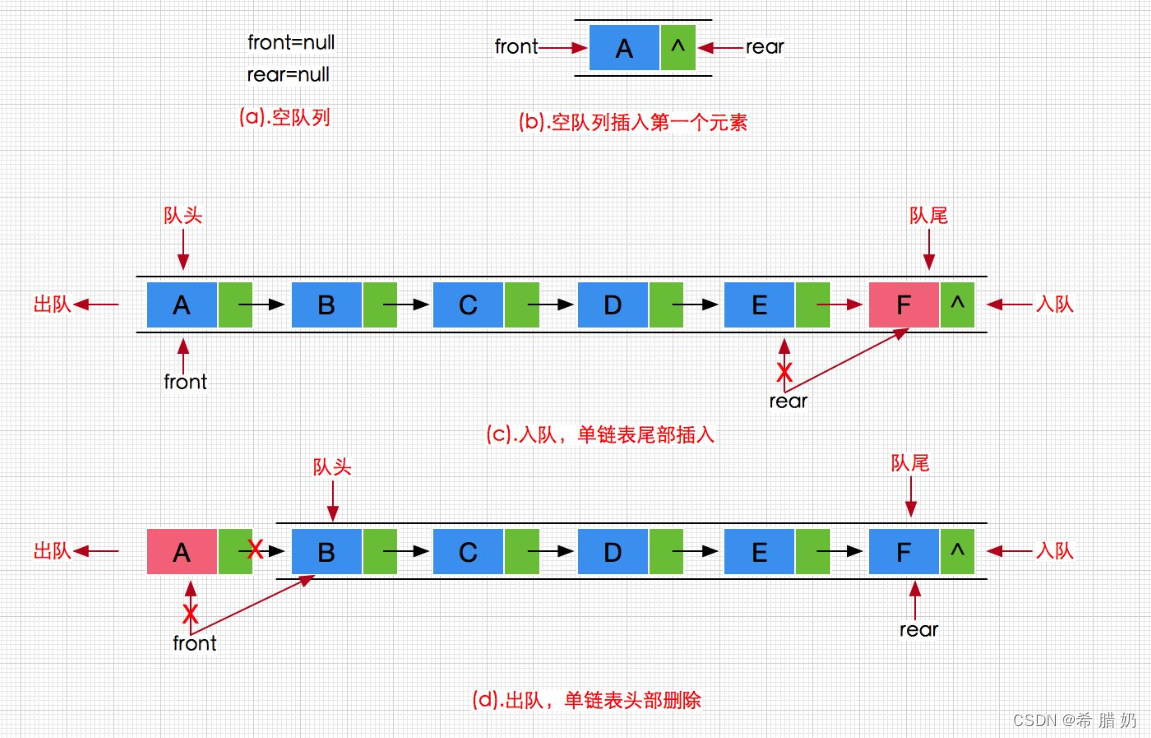
                        下面话不多说，直接开始代码实现

                        1、队列的链式结构设计

                        //链式结构 表示队列
typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType val;                           
}QNode;
//队列的结构
typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

                        2、常用的功能接口

                        //初始化
void QueueInit(Queue* pq);
//销毁队列
void QueueDeatroy(Queue* pq);
//队尾入列
void QueuePush(Queue* pq, QDataType x);
//队头出列
void QueuePop(Queue* pq);
//获取队列头部元素
QDataType QueueFront(Queue* pq);
//获取队列尾部元素
QDataType QueueBack(Queue* pq);
//检测队列是否为空，如果为空返回非零结果，如果非空返回0 
bool QueueEmpty(Queue* pq);
//获取队列中有效元素个数
int QueueSize(Queue* pq);
                        2.1、初始化队列

                        只需要将头尾指针都指向空即可，元素个数为零

                        //初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}
                        2.2、销毁队列

                        遍历链表，从头到尾依次删除结点，最后将头尾指针指向空，元素个数为0。

                        //销毁队列
void QueueDeatroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
	
}
                        2.3、入队列

                        创建新节点，若队列为空，则将头指针和尾指针都指向新创建的节点，若不为空，则尾插，因为是链式存储，所以和单链表的尾插一样，将尾指针的next指向该节点，再把该节点设为新的尾节点

                        void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newnode->val = x;
	newnode->next = NULL;
	if (pq->ptail == NULL)
	{
		pq->ptail = pq->phead = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}
                        2.4、出队列

                        注意：出列要考虑队列是空还是只有一个结点又或者有多个结点，为空则在代码第一步就报错，若只有一个结点，则直接删除该结点，并将头尾俩指针指向空，若不止一个结点，可以创建一个临时指针来记录当前头指针，然后尾指针往后遍历，再free掉创建的临时指针，并置空

                        void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	QNode* del = pq->phead;
	pq->phead = pq->phead->next;
	free(del);
	del = NULL;
	if (pq->phead == NULL)
		pq->ptail = NULL;
	pq->size--;
}
                        2.5、获取队列头部元素

                        断言，然后直接返回队头指针指向的节点元素

                        //获取队列头部元素
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->val;
}
                        2.6、获取队列尾部元素

                        也是一样的，直接返回队尾指针指向的节点元素

                        //获取队列尾部元素
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->ptail->val;
}
                        2.7、判空

                        检测队列是否为空，如果为空返回非零结果，如果非空返回0

                        bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}
                        2.8、获取有效元素个数
                        //获取队列中有效元素个数
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

                        完整代码

                        Queue.h

                        #include
#include
#include
#include
//链式结构 表示队列
typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType val;                           
}QNode;
//队列的结构
typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;
//初始化
void QueueInit(Queue* pq);
//销毁队列
void QueueDeatroy(Queue* pq);
//队尾入列
void QueuePush(Queue* pq, QDataType x);
//队头出列
void QueuePop(Queue* pq);
//获取队列头部元素
QDataType QueueFront(Queue* pq);
//获取队列尾部元素
QDataType QueueBack(Queue* pq);
//检测队列是否为空，如果为空返回非零结果，如果非空返回0 
bool QueueEmpty(Queue* pq);
//获取队列中有效元素个数
int QueueSize(Queue* pq);

                        Queue.c

                        #include"Queue.h"
//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}
//销毁队列
void QueueDeatroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
	
}
//队尾入列
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->next = NULL;
	newnode->val = x;
	if (pq->ptail == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
	else
	{
		//现在newnode是新的尾结点
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}
//队头出列
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->phead); 
	//保存当前节点
	QNode* tmp = pq->phead;
	//phead往下走
	pq->phead = pq->phead->next;
	free(tmp);
	tmp = NULL;
	if (pq->phead = NULL)
	{
		pq->ptail = NULL;
	}
	pq->size--;
}
//获取队列头部元素
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->val;
}
//获取队列尾部元素
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->ptail;
}
//检测队列是否为空，如果为空返回非零结果，如果非空返回0 
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}
//获取队列中有效元素个数
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

                        Test.c

                        #include"Queue.h"
int main()
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, 1);
	QueuePush(&q, 2);
	QueuePush(&q, 3);
	while (!QueueEmpty(&q))
	{
		printf("%d ", QueueFront(&q));
		QueuePop(&q);
	}
	QueueDeatroy(&q);
	return 0;
}

                        【数据结构】栈和队列超详解！(Stack && Queue),在这里插入图片描述,第8张

                         

    上一篇：初级数据结构（七）——二叉树

    下一篇：数学基础--均值、方差、标准差、协方差

    网站优化运营
    整站seo优化
    网络营销运营
    成功案例
    品牌创意网站
    营销型网站
    小程序
    微信小程序
    微信公众号
    百度熊掌号
    网站优化分享
    关于我们
    公司概况
    公司新闻
    公司文化
    结构体系
    企业资质
    加入我们
    关注我们
    扫描二维码
    获取更多信息
    精彩一手掌握
    Copyright © 2014-2019 seo,上海网站优化_网络制作_网站seo排名_网站建设推广_上海网络公司 版权所有 沪ICP备19022315号