分治算法总结（Java）_网站优化分享

您的位置：上海毫米网络优化公司 > 网站优化分享 >

分治算法概述

分治：即分而治之。也就是将一个大的问题拆分为若干个小问题，然后递归解决每个小问题，最终合并每个小问题的解得到原问题的解

分治算法总结（Java）,第1张

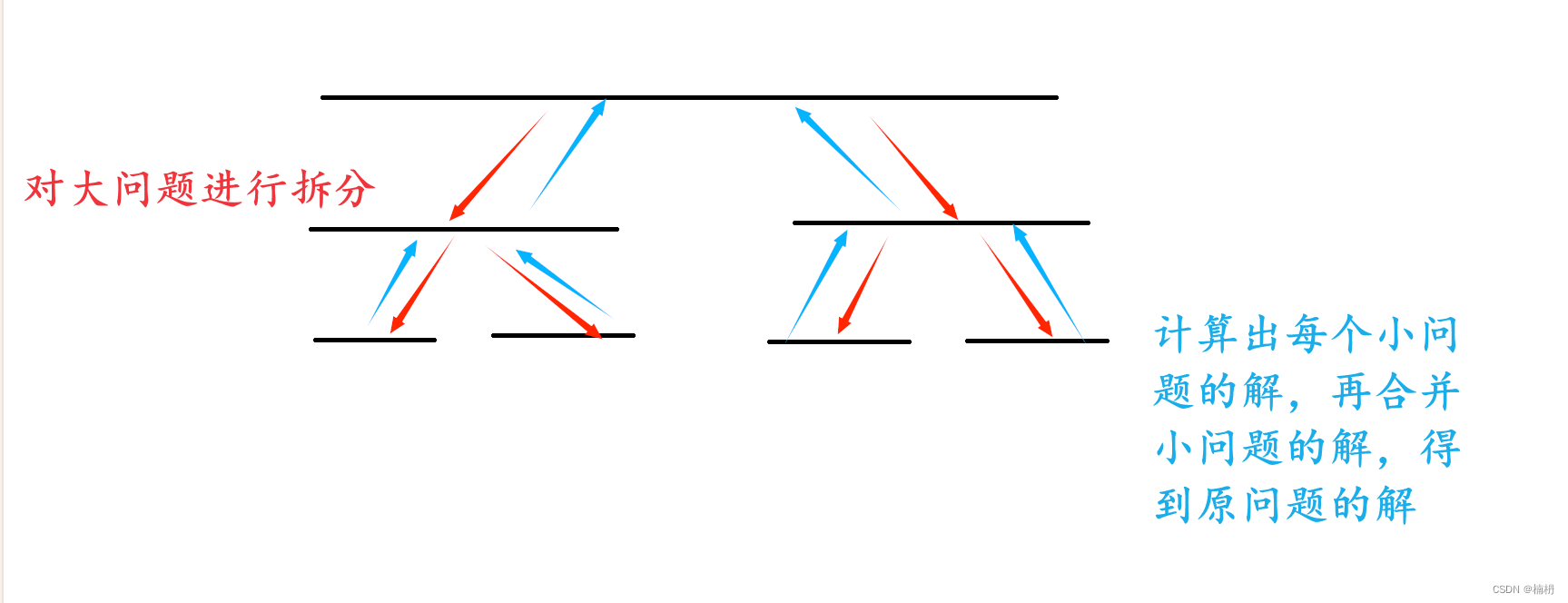
分治算法一般包含三步：

1. 分割问题：将原问题分割为若干子问题，这些子问题应该是相互独立的，并且和原问题具有相同的结构。

2. 解决子问题：递归解决每个子问题，当子问题足够小时，直接求解

3. 合并子问题的解：将子问题的解合并成原问题的解。

分治的思想体现在快速排序、归并、二分查找等中，在本篇文章中，我们重点讲解其在快速排序和归并中的使用。

快速排序

快速排序：用于对数组进行排序，其基本思想是选择一个基准元素，通过将数组中的其他元素按照与基准元素的大小关系分为两个（或三个）子数组，然后递归地对这两个（或三个）子数组进行排序，最终将整个数组排序完成。

在分割数组时，可以将数组中的其他元素按照与基准元素的大小关系分为两个子数组，一个子数组中的元素都小于基准元素，另一个子数组中的元素都大于等于基准元素。也可以分为三个子数组，其中，一个子数组中的元素都小于基准元素，一个子数组中的元素都等于基准元素，一个子数组中的元素都大于基准元素。

分治算法总结（Java）,第2张

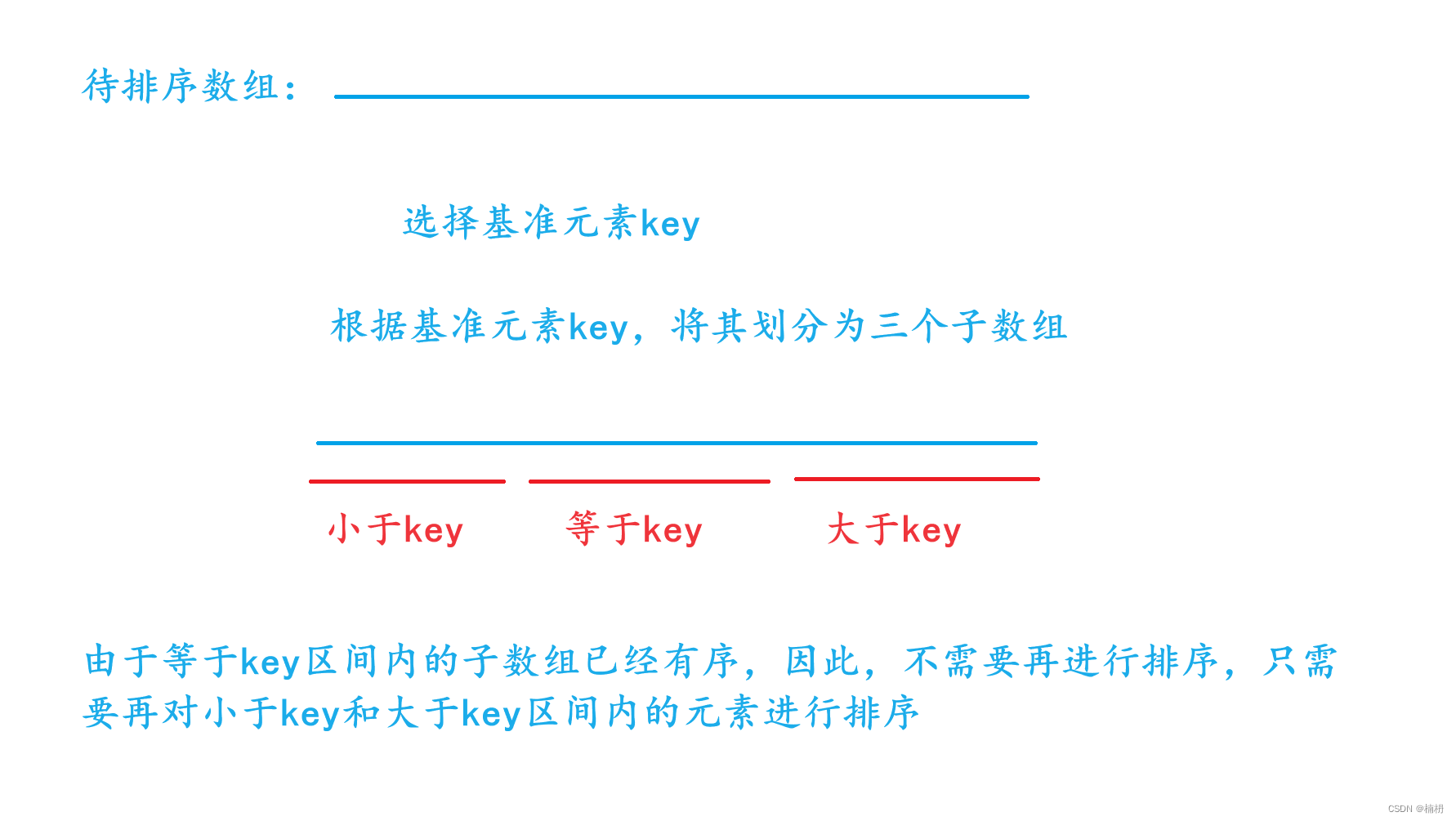
当将数组分为三块时，等于key区间内的元素已经有序，因此，只需递归排序左边部分和右边部分。当数据中有很多重复数据时，排序效率会大大提升

接下来，我们以一些练习来进一步掌握快速排序

练习1：排序数组

题目链接：

912. 排序数组 - 力扣（LeetCode）

题目描述：

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

提示：

1 <= nums.length <= 5 * 104

-5 * 104 <= nums[i] <= 5 * 104

思路分析：

在这里，我们使用快速排序来对数组进行排序，具体实现步骤为：

1. 选择基准元素：从数组中选择一个元素作为基准元素

那么，该如何选择基准元素呢？

我们可以选择第一个元素作为基准元素，也可以取中间元素作为基准元素，还可以比较第一个元素、中间元素和最后一个元素的大小，选择中间大小的元素作为基准元素。但，从数组中选择元素，我们应该做到随机选择一个元素，因此，我们可以使用随机数来选择基准元素。

2. 分割数组：在这里我们将数组分为三个子数组，其中元素分别为：小于基准元素、等于基准元素和大于基准元素

如何将当前数组中的元素划分为三个部分？

我们可以利用双指针的思想来进行划分，但仅仅使用两个指针无法完成三部分的划分，在这里，要使用三个指针。分别定义left和right，再定义变量i来遍历数组，因此这三个变量将数组划分为四个区间：

分治算法总结（Java）,第3张

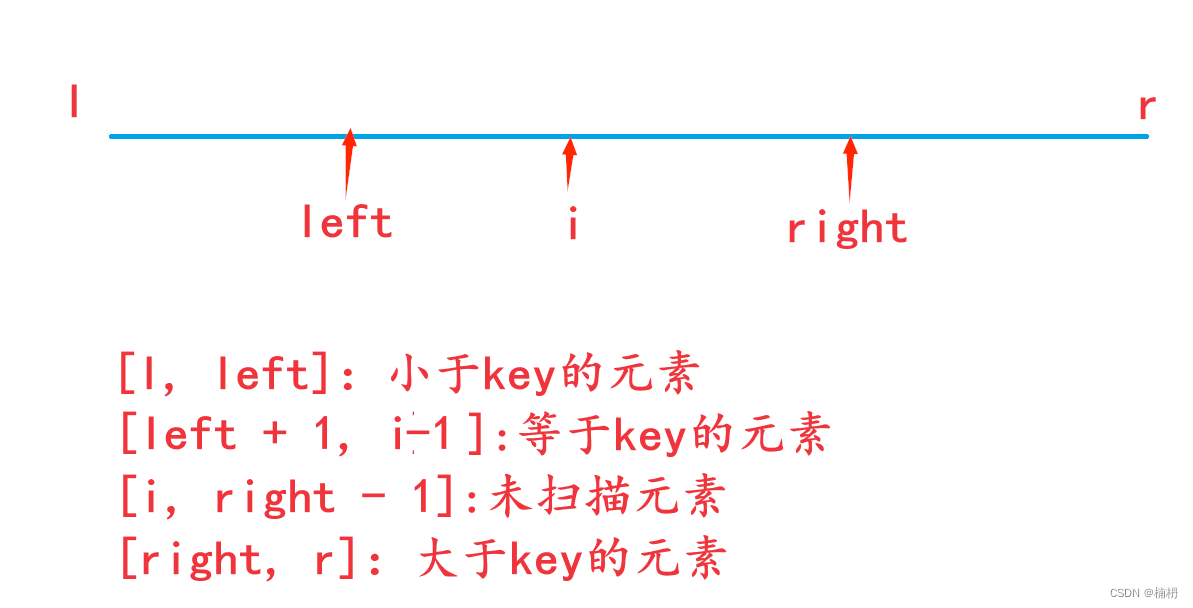
i扫描到的元素可能有三种情况：

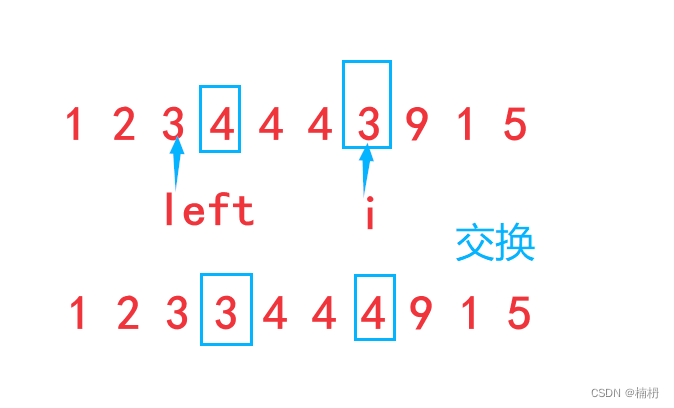
1. 小于key：此时需要将其放入[l, left]区间内，因此需要将当前元素和left+1位置元素交换，再将left向后移动一位，即可将其放入[l, left]区间内。由于left+1位置元素是等于key的元素，将其交换到i位置后，left + 2到i位置的元素都等于key，此时即可将left向右移动一位，i也可以向右移动一位，继续扫描下一个元素

分治算法总结（Java）,第4张

2. 等于key：此时需要将其放入[left + 1, i]区间内，因此只需将 i 向后移动一位（i++），即可将其放入[left + 1, i]区间内

3. 大于key：此时需要将其放入[right, r]区间内，因此需要将当前元素与right -1位置元素进行交换，此时再将right - 1，即可将其放入[right, r]区间内，但由于[i, right-1]区间内的元素是未排序元素，因此，不能移动i，要继续判断此时i位置上元素与key的大小关系

当i等于right时，此时数组被划分为三个区间，循环结束

3. 递归排序：由于等于基准元素的子数组已经有序，因此，我们只需对小于基准元素和大于基准元素的子数组分别递归应用快速排序算法，直到子数组的长度为1或者0，此时子数组已经有序。

4. 合并结果：将排序好的子数组合并，即可得到整个数组的有序序列。

代码实现：

class Solution {
    public int[] sortArray(int[] nums) {
        sort(nums, 0, nums.length - 1);
        return nums;
    }
    private void sort(int[] nums, int l, int r){
        if(l >= r) return;//递归结束
        int key = nums[new Random().nextInt(r - l + 1) + l];//利用随机数来选择基准元素
        //将数组分为三块
        int left = l - 1, right = r + 1, i = l;
        while(i < right){//注意：条件为 i < right，而不是i < nums.length
            if(nums[i] < key) swap(nums, ++left, i++);
            else if(nums[i] == key) i++;
            else swap(nums, --right, i);
        }
        //继续递归排序左区间和右区间
        sort(nums, l, left);
        sort(nums, right, r);
    }
    private void swap(int[] nums, int a, int b){
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }
}

练习2：数组中的第K个最大元素

题目链接：

215. 数组中的第K个最大元素 - 力扣（LeetCode）

题目描述：

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示：

1 <= k <= nums.length <= 105

-104 <= nums[i] <= 104

思路分析：

要求数组中第K个最大的元素，我们可以想到使用堆排序，建立大小为k 的小根堆，遍历数组，若当前元素大于堆顶元素，就将堆顶元素弹出，再将该元素放入堆中，遍历完后，小根堆堆顶元素即为第K个最大的元素

堆排序代码实现：

class Solution {
    public int findKthLargest(int[] nums, int k) {
        //建立小根堆
        PriorityQueue priorityQueue = new PriorityQueue<>(new Comparator() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1 - o2;
            }
        });
        for (int i = 0; i < nums.length; i++) {
            if(priorityQueue.size() < k){//当小根堆未满时，直接向其中添加元素
                priorityQueue.add(nums[i]);
            }else {//当小根堆满时，需判断是否需要更新元素
                if(priorityQueue.peek() < nums[i]){//若当前元素大于堆顶元素，弹出堆顶元素，放入当前元素
                    priorityQueue.poll();
                    priorityQueue.add(nums[i]);
                }
            }
        }
        return priorityQueue.peek();
    }
}

我们也可以使用快速排序来找到数组中第K个最大的元素：

我们首先通过基准元素key将数组划分为三块，设三个区间内的元素个数分别为a b c

分治算法总结（Java）,第5张

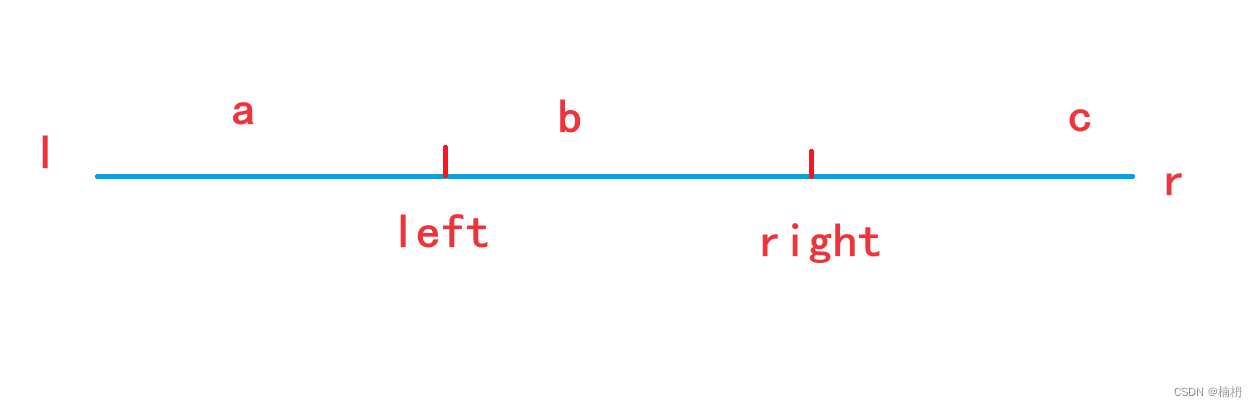
再判断第k个最大的数落在哪个区间内

由于要找的是最大的第K个数，因此，我们先判断右侧（包含较大数）的区间，再判断中间和左边

若k <= c：此时第K个最大的元素落在[right, r]区间内，我们需要继续在[right, r] 区间内找第K个最大的元素

若 k > c 且 k >= c + b，此时第K个最大的元素落在[left + 1, right - 1]区间内，即第k个最大的元素为基准元素key，直接返回即可

若k <= a，此时第K个最大的元素落在[l, left]区间内，我们需要继续在[l, left] 区间内找，但此时，我们要在[l, left]区间内找的是：第 k - a - b个最大的元素，即直接排除大于key和等于key的所有元素

代码实现：

class Solution {
    public int findKthLargest(int[] nums, int k) {
        return sort(nums, 0, nums.length - 1, k);
    }
    private int sort(int[] nums, int l, int r, int k){
        if(l >= r) return nums[l];//递归结束
        //随机选择基准元素
        int key = nums[new Random().nextInt(r - l + 1) + l];
        //将数组划分为三块
        int left = l - 1, right = r + 1, i = l;
        while(i < right){
            if(nums[i] < key) swap(nums, ++left, i++);
            else if(nums[i] == key) i++;
            else swap(nums, --right, i);
        }
        //判断第k个最大的元素在哪个区间
        int c = r - right + 1, b = right - left - 1;
        if(c >= k) return sort(nums, right, r, k);//在右区间继续寻找第k个最大的元素
        else if(c + b >= k) return key;//第k个最大的元素为k，直接返回
        else return sort(nums, l, left, k - b - c);//在左区间继续寻找
    }
    private void swap(int[] nums, int a, int b){
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }
}

练习3：最小k个数

题目链接：

面试题 17.14. 最小K个数 - 力扣（LeetCode）

题目描述：

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

提示：

0 <= len(arr) <= 100000

0 <= k <= min(100000, len(arr))

思路分析：

同样的，这道题也可以利用大根堆来找到最小的k个数

堆排序代码实现：

class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] ret = new int[k];
        //判断特殊情况
        if(arr.length <= 0 || k <= 0) return ret;
        //建立大根堆
        PriorityQueue priorityQueue = new PriorityQueue<>(new Comparator() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        for (int i = 0; i < arr.length; i++) {
            if(priorityQueue.size() < k){//当大根堆未满时，直接向其中添加元素
                priorityQueue.add(arr[i]);
            }else {//当大根堆满时，需判断是否需要更新元素
                if(priorityQueue.peek() > arr[i]){//若当前元素小于堆顶元素，弹出堆顶元素，放入当前元素
                    priorityQueue.poll();
                    priorityQueue.add(arr[i]);
                }
            }
        }
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }
        return ret;
    }
}

由于可以以任意顺序返回这k个数，因此，我们也可以利用快速排序来找到这最小的k个数，本题的解题思路与练习2类似，唯一不同的是：本题需要返回一个大小为k的数组

因此，我们创建一个大小为k的数组ret

同样的，通过基准元素key将数组划分为三块，设三个区间内的元素个数分别为a b c

接下来，在判断这k个数在哪个区间内：

由于我们要找的是最小的k个数，因此我们先判断左边（较小元素所在区间），再判断中间和右边

若 k < a，则最小的k个数都在小于key的区间内，因此我们继续在[l, left]区间内找最小k个数

若k >= a 且 k <= a + b，则最小的k个数包含[l, left]区间所有元素和部分 [left + 1, right - 1]区间内元素，因此，我们只需将这k个元素放入ret中，就找到了最小k个数

若k > a + b，此时最小的k个数包含[l, right - 1]区间内所有元素，因此，我们先将这 a + b个元素放入ret中，再在[right, r]中找剩下k - a - b个数

由于经过快排后，数组中前k个元素就是最小的k个数，因此我们可以在快速排序结束后，将这k个数放入ret中并返回

代码实现：

class Solution {
    public int[] smallestK(int[] arr, int k) {
        findsmall(arr, 0, arr.length - 1, k);
        int[] ret = new int[k];
        for (int i = 0; i < k; i++) {
            ret[i] = arr[i];
        }
        return ret;
    }
    
    private void findsmall(int[] arr, int l, int r, int k){
        if(l >= r) return;//递归结束
        //随机选择基准元素
        int key = arr[new Random().nextInt(r - l + 1) + l];
        //数组分三块
        int left = l - 1, right = r + 1, i = l;
        while(i < right){
            if(arr[i] < key){
                swap(arr, ++left, i++);
            }else if(arr[i] == key){
                i++;
            }else {
                swap(arr, --right, i);
            }
        }
        //分情况讨论
        int a = left - l + 1, b = right - left - 1;
        if(k < a) findsmall(arr, l, left, k);
        else if(k <= a + b) return;
        else findsmall(arr, right, r, k - a - b);
    }
     private void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

归并排序

归并排序：用于对一个数组进行排序。它的基本思想是将数组划分为两个子数组，递归地对这两个子数组进行排序，最终将两个有序的子数组合并成一个有序的数组。

分治算法总结（Java）,第6张

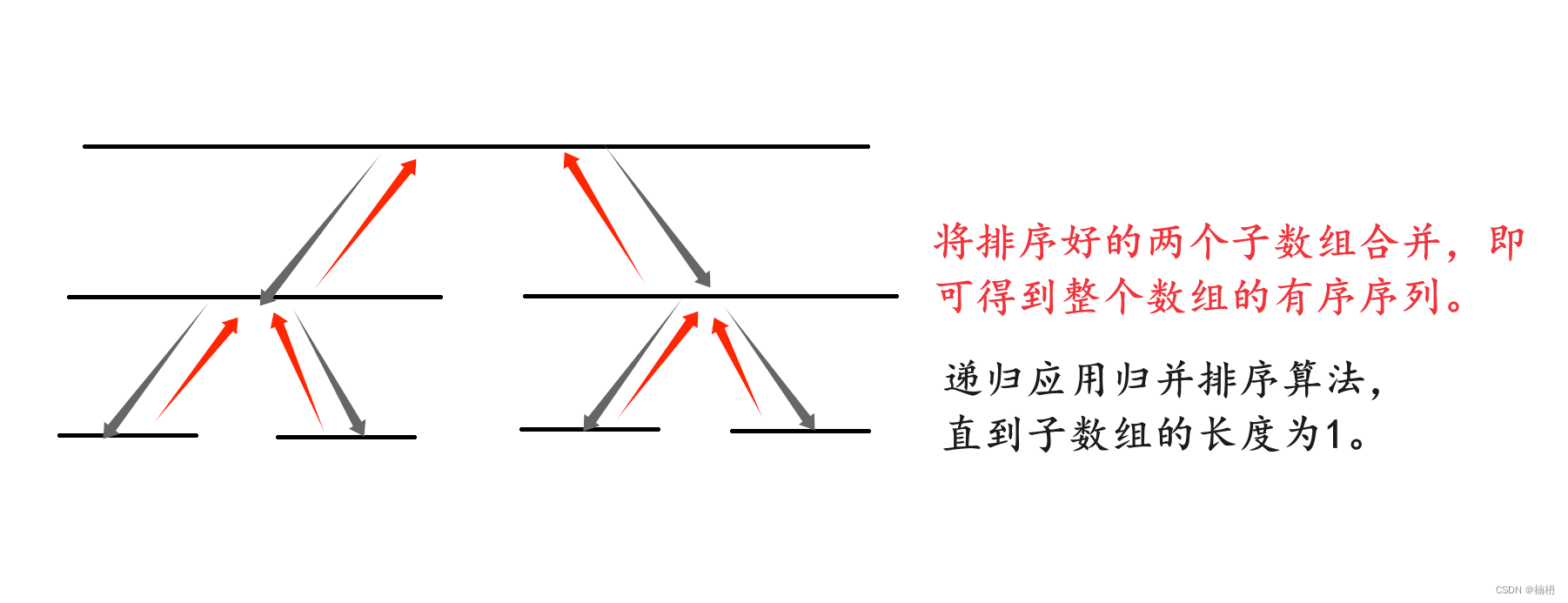
归并排序的解题步骤为：

1. 分割数组：将数组平均分成两个子数组，直到每个子数组只包含一个元素。

2. 递归排序：对两个子数组分别递归地应用归并排序算法，直到子数组的长度为1。

3. 合并结果：：将排序好的两个子数组合并，即可得到整个数组的有序序列。在合并时，可使用双指针或额外数组来完成合并

接下来，我们以几道练习来进一步掌握归并排序

练习4：排序数组

题目链接：

912. 排序数组 - 力扣（LeetCode）

题目描述：

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

提示：

1 <= nums.length <= 5 * 104

-5 * 104 <= nums[i] <= 5 * 104

思路分析：

在这里，我们使用归并排序来解决本题。

首先我们进行拆分：将数组一分为二分为两部分，直到分解到数组的长度为1，使整个数组的排序过程被分为左半部分排序 + 右半部分排序

接下来我们进行合并：将两个较短的有序数组合并成一个长的有序数组，一直合并到最初的长度

如何合并两个较短的有序数组？

我们可以使用一个新的数组保存临时结果，再使用两个指针分别指向两个较短数组的起始位置，然后判断两指针所指元素大小，谁小就将其放入临时数组中，再向后移动，这样，就将合并结果放入临时数组中，然后再将临时数组中的元素放入原数组中，即可合并两个有序数组

分治算法总结（Java）,第7张

代码实现：

class Solution {
    int[] temp;//为了节省额外的空间开销，我们将临时数组定义为成员变量
    public int[] sortArray(int[] nums) {
        temp = new int[nums.length];
        mergerSort(nums, 0, nums.length - 1);
        return nums;
    }
    private void mergerSort(int[] nums, int left, int right){
        if(left >= right) return;//只有一个元素时，递归结束
        int mid = (left + right) / 2;//以中间元素划分左右区间
        mergerSort(nums, left, mid);//继续递归，将左右子区间排好序
        mergerSort(nums, mid + 1, right);
        int cur1 = left, cur2 = mid + 1, i = left;//合并两个有序数组
        while(cur1 <= mid && cur2 <= right){
            temp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];
        }
        //将未变量完的数组元素放入temp中
        while(cur1 <= mid) temp[i++] = nums[cur1++];
        while(cur2 <= right) temp[i++] = nums[cur2++];
        //将temp中数据更新到nums中
        for(int j = left; j <= right; j++){
            nums[j] = temp[j];
        }
    }
}

练习5：交易逆序对的总数

题目链接：

LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

题目描述：

在股票交易中，如果前一天的股价高于后一天的股价，则可以认为存在一个「交易逆序对」。请设计一个程序，输入一段时间内的股票交易记录 record，返回其中存在的「交易逆序对」总数。

示例 1:

输入：record = [9, 7, 5, 4, 6]
输出：8
解释：交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。

限制：

0 <= record.length <= 50000

思路分析：

首先我们可以想到暴力枚举，即计算每个数的逆序对，再相加，即可求出总的逆序对的个数。但其时间复制度为O（n^2），很有可能超出时间限制。接下来，我们考虑能否使用归并排序来解决该问题，我们可以利用归并排序中两个较短的有序数组来快速统计出逆序对的个数

若有序数组为升序：

由于要前一个元素大于后一个元素才能构成逆序对（a, b）且此时数组为升序，因此，我们可以以右半部分元素b为基准，找到左半部分所有大于当前元素a的元素。当左半部分第一次出现比b大的元素a时，说明左半部分中当前元素到右边界的元素都比b大，此时就可直接计算出b可以构成的逆序对，此时右半部分的指针再向后移动一位到元素c，左半部分的指针也不必回退到起始位置（由于a前面的元素都比b小，不能构成逆序对，c >= b，则a前面的元素也不可能和c构成逆序对）

分治算法总结（Java）,第8张

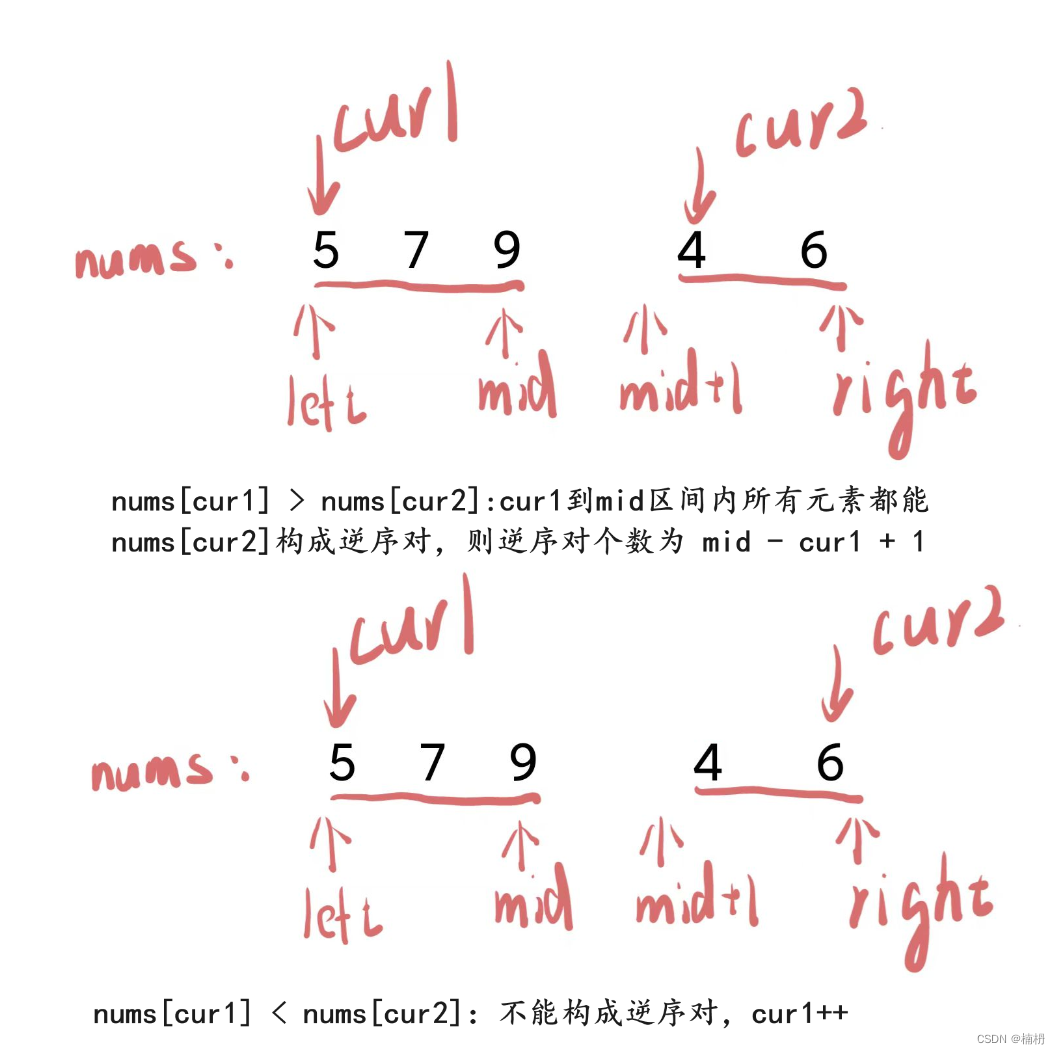
即：nums[cur1] > nums[cur2] ret(逆序对总数) += (mid - cur1 + 1), cur2++

nums[cur1] <= nums[cur2] cur1++

能否以左半部分元素a为基准呢？

若以左半部分元素a为基准，我们需要在右半部分找到所有小于a的元素，此时，当第一次出现大于或等于a的元素b，说明 b 到右边界 right 的所有元素均不能构成逆序对，因此小于a的元素为 mid+1 到当前元素位置 - 1的所有元素，

即：nums[cur2] >= nums[cur1] ret += cur2 - (mid + 1) cur1++

nums[cur2] < nums[cur1] cur2++

但，若右半部分区域没有大于或等于a的元素b，此时cur2直接移动到最右端，此时退出循环，未统计所有逆序对，因此，若要使用这种方法，还需要判断边界情况，较为复杂，因此不推荐使用

若有序数组为降序：

同样的，由于要前一个元素大于后一个元素才能构成逆序对（a, b），且此时有序数组为降序，因此，我们以左半部分元素a为基准，找到右半部分中比a小的所有元素。当右半部分第一次出现小于a的元素b，则右半部分当前元素cur2 到右边界right 的所有元素都小于a，则可求出a能构成的逆序对。

因此：nums[cur2] < nums[cur1] ret(逆序对总数) += (right - cur2 + 1), cur1++

nums[cur2] >= nums[cur1] cur2++

代码实现：

升序：

class Solution {
    int[] temp;
    public int reversePairs(int[] record) {
        temp = new int[record.length];
        return mergerSort(record, 0, record.length - 1);
    }
    private int mergerSort(int[] nums, int left, int right){
        if(left >= right) return 0;//当只有一个元素或没有元素时，递归结束，此时无逆序对，返回0
        int mid = (left + right) / 2;
        int ret = 0;//计算总的逆序对个数
        //递归，求左半部分逆序对的个数 和 右半部分逆序对的个数
        ret += mergerSort(nums, left, mid);
        ret += mergerSort(nums, mid + 1, right);
        //求 左半部分 与 右半部分构成的逆序对，同时进行排序(此时为升序)
        int cur1 = left, cur2 = mid + 1, i = left;
        while(cur1 <= mid && cur2 <= right){
            if(nums[cur1] > nums[cur2]){
                ret += mid - cur1 + 1;
                temp[i++] = nums[cur2++];
            }else{
                temp[i++] = nums[cur1++];
            }
        }
        //将剩余元素放入temp中
        while(cur1 <= mid) temp[i++] = nums[cur1++];
        while(cur2 <= right) temp[i++] = nums[cur2++];
        //将排序结果更新到nums中
        for(int j = left; j <= right; j++){
            nums[j] = temp[j];
        }
        return ret;
    }
}

降序：

class Solution {
    int[] temp;
    public int reversePairs(int[] record) {
        temp = new int[record.length];
        return mergerSort(record, 0, record.length - 1);
    }
    private int mergerSort(int[] nums, int left, int right){
        if(left >= right) return 0;//当只有一个元素或没有元素时，递归结束，此时无逆序对，返回0
        int mid = (left + right) / 2;
        int ret = 0;//计算总的逆序对个数
        //递归，求左半部分逆序对的个数 和 右半部分逆序对的个数
        ret += mergerSort(nums, left, mid);
        ret += mergerSort(nums, mid + 1, right);
        //求 左半部分 与 右半部分构成的逆序对，同时进行排序(此时为降序)
        int cur1 = left, cur2 = mid + 1, i = left;
        while(cur1 <= mid && cur2 <= right){
            if(nums[cur2] < nums[cur1]){
                ret += right - cur2 + 1;
                temp[i++] = nums[cur1++];
            }else{
                temp[i++] = nums[cur2++];
            }
        }
        //将剩余元素放入temp中
        while(cur1 <= mid) temp[i++] = nums[cur1++];
        while(cur2 <= right) temp[i++] = nums[cur2++];
        //将排序结果更新到nums中
        for(int j = left; j <= right; j++){
            nums[j] = temp[j];
        }
        return ret;
    }
}

练习6：计算右侧小于当前元素的个数

题目链接：

315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

题目描述：

给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例 1：

输入：nums = [5,2,6,1]
输出：[2,1,1,0] 
解释：
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素

示例 2：

输入：nums = [-1]
输出：[0]

示例 3：

输入：nums = [-1,-1]
输出：[0,0]

提示：

1 <= nums.length <= 105

-104 <= nums[i] <= 104

思路分析：

本题与练习5 类似，都要求后面的元素小于前面的元素，但不同的是，本题要返回一个新的数组，且数组中存放的是原数组中每个元素右侧小于 nums[i] 的元素数量

那么应该如何处理呢？

归并排序后会打乱数组原有的顺序，因此我们要解决的问题就是如何找到数组元素原有的位置，在这里我们可以使用一个下标数组index，来记录每个元素的下标，然后将下标数组 index 和原数组 nums 绑定在一起，一起移动，这样，就算数组重新进行排序，也能够通过下标数组找到元素原位置

分治算法总结（Java）,第9张

此时我们创建一个新的数组ret 保存原nums[i]右侧小于nums[i]的元素数量，在合并两个有序数组时，计算出 nums[k] 的右侧小于当前元素的个数 count 后，利用数组下标找到该元素原有下标：index[k]，再将结果更新到数组ret中：ret[index[k]] += count

代码实现：

class Solution {
    int[] ret;
        int[] index;//下标数组
        int[] tempNums;//临时数组
        int[] tempIndex;//临时下标数组
        
    public List countSmaller(int[] nums) {
       int n = nums.length;//数组长度
       ret = new int[n];
       index = new int[n];
       tempNums = new int[n];
       tempIndex = new int[n]; 
       //初始化下标数组
       for(int i = 0; i < n; i++){
           index[i] = i;
       }
       //归并排序
       mergerSort(nums, 0, n - 1);
       //将结果放入list中
       List list = new ArrayList<>();
       for(int x: ret) list.add(x);
       return list;
    }
    private void mergerSort(int[] nums, int left, int right){
        if(left >= right) return;//当只有一个元素或没有元素时，没有小于该元素的元素，直接返回
        int mid = (left + right) / 2;//根据中间元素将数组划分为两个区间
        //递归处理左区间和右区间
        mergerSort(nums, left, mid);
        mergerSort(nums, mid+1, right);
        //求左半部分元素 在 右半部分中 有多少个元素比其小
        //因此我们对数组降序排列
        int cur1 = left, cur2 = mid + 1, i = left;
        while(cur1 <= mid && cur2 <= right){
            if(nums[cur1] > nums[cur2]){
                ret[index[cur1]] += right - cur2 + 1;//更新当前元素的 右侧小于该元素 的个数
                tempNums[i] = nums[cur1];//将元素放入临时数组中
                tempIndex[i++] = index[cur1++];//注意：该元素的下标也要同步进行保存
            }else{
                tempNums[i] = nums[cur2];
                tempIndex[i++] = index[cur2++];
            }
        }
        //将剩余元素放入临时数组中
        while(cur1 <= mid){
            tempNums[i] = nums[cur1];
            tempIndex[i++] = index[cur1++];
        }
        while(cur2 <= right){
            tempNums[i] = nums[cur2];
            tempIndex[i++] = index[cur2++];
        }
        //将数据更新到nums和index中
        for(int j = left; j <= right; j++){
            nums[j] = tempNums[j];
            index[j] = tempIndex[j];
        }
    }
}

练习7：翻转对

题目链接：

493. 翻转对 - 力扣（LeetCode）

题目描述：

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

示例 1:

输入: [1,3,2,3,1]
输出: 2

示例 2:

输入: [2,4,3,5,1]
输出: 3

注意:

给定数组的长度不会超过50000。
输入数组中的所有数字都在32位整数的表示范围内。

思路分析：

本题同样与练习5类似，但此时 nums[i] > 2*nums[j]，即要满足当前元素大于右侧元素的两倍，或当前元素小于左侧元素的一半。在这里仍可以使用归并排序来解决该问题，此时我们使用降序排列，以左半部分元素为基准，在右半部分中找小于该元素的所有元素。由于这里判断的条件为 nums[i] > 2*nums[j]，因此，我们不能再边计算结果边排序（当前元素小于右侧元素的2倍，但不一定小于右侧元素，如：5 < 2*3 但 5 > 3），因此，我们需要先计算翻转对的个数，再进行排序。

代码实现：

class Solution {
    int[] temp;
    public int reversePairs(int[] nums) {
        temp = new int[nums.length];
        return mergerSort(nums, 0, nums.length - 1);
    }
    private int mergerSort(int[] nums, int left, int right){
        if(left >= right) return 0;//递归结束
        int mid = (left + right) / 2;
        //继续递归
        int ret = 0;
        ret += mergerSort(nums, left, mid);
        ret += mergerSort(nums, mid + 1, right);
        //计算翻转对
        //当前元素后，有多少个元素的二倍小于当前元素
        int cur1 = left, cur2 = mid + 1, i = left;
        while(cur1 <= mid && cur2 <= right){
            //虽然所有元素的大小都在int类型范围内，但2倍后却有可能溢出，因此要使用long类型
            if((long)nums[cur1] > (long)2 * nums[cur2]){//也可以判断 当前元素的一半是否大于 右侧元素 nums[cur1] / 2.0 > nums[cur2]
                ret += (right - cur2 + 1);
                cur1++;
            }else{
                cur2++;
            }
        }
        //降序排序
        cur1 = left; cur2 = mid+1;
        while(cur1 <= mid && cur2 <= right){
            if(nums[cur1] > nums[cur2]){
                temp[i++] = nums[cur1++];
            }else{
                temp[i++] = nums[cur2++];
            }
        }
        //将剩余元素放入temp中
        while(cur1 <= mid){
            temp[i++] = nums[cur1++];
        }
        while(cur2 <= right){
            temp[i++] = nums[cur2++];
        }
        //将排序后的元素放入nums中
        for(int j = left; j <= right; j++){
            nums[j] = temp[j];
        }
        return ret;
    }
}

网站规划包括哪些内容长沙大型网站设计公司企业网络推广冷门行业发生过的凶案推广软件哪个好企业网站官网建设

上一篇：20道真题训练|学会二叉树的前世今生(三)

下一篇：Warp算法OpenCL异构开发总结