原题详细如下：

n− 皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

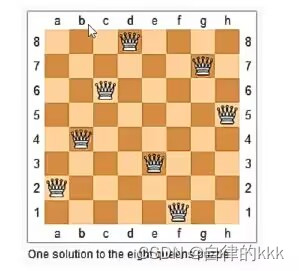
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..

...Q

Q...

..Q.

..Q.

Q...

...Q

.Q..

解题思路：

从每一行开始，遍历一这行的所有元素，如果这一行的列，正对角，反对角都没有皇后，就在这个位置放入一个皇后，然后继续向下一行进行搜索。

对角坐标如下图：

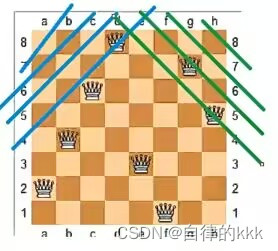
（蓝色为正对角，绿色为反对角，

故正对角线的坐标为：当前行+当前列，

反对角坐标为：n-当前行+当前列。

代码如下：

#include
using namespace std;
const int N = 20;
int n;
bool y[N], dg[N], udg[N]; //分别对应列，正对角，反对角
char p[N][N];
void dfs(int u)
{
	if (u == n)
	{
		//如果成功搜索到最后一行，就说明已经找到了一个方案，就把这个方案输出
		for (int i = 0; i < n; i++)cout << p[i] << endl;
		cout << endl;
		return;
	}
	for (int i = 0; i < n; i++)
	{
		//遍历这一行当中得元素，如果这一列以及两个对角都没有皇后，就在这个坐标放入一个皇后
		if (!y[i] && !dg[u + i] && !udg[n - u + i]) 
		{
			p[u][i] = 'Q';
			y[i] = dg[u + i] = udg[n - u + i] = true;
			dfs(u + 1); //放完后继续向下一行搜索
			//搜索完之后回溯要把数据还原
			p[u][i] = '.';  
			y[i] = dg[u + i] = udg[n - u + i] = false;
		}
	}
}
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			p[i][j] = '.';
	dfs(0);
	return 0;
}

DFS解n皇后问题

算法小白的学习笔记。