- XGBOOST算法Python实现(保姆级)
- MySQL-触发器(TRIGGER)
- 掌握Go语言:Go语言类型转换,无缝处理数据类型、接口和自定义类型的转
- 【数据库】国产达梦数据库与mysql特点、区别、发展前景
- Go-Zero微服务快速入门和最佳实践(一)
- Springboot 整合 Quartz(定时任务框架)
- Vue实例挂载的过程
- 数据结构中的时间复杂度和空间复杂度基础
- SpringBoot(java)实现websocket实现实时通信
- mysql中find
- Spring Boot最经典的20道面试题,你都会了吗?
- Mysql时间差8小时解决方案
- 志愿服务管理小程序设计与实现 毕业设计-附源码97923
- Java校园失物招领系统设计与实现(Idea+Springboot+m
- golang工程——opentelemetry简介、架构、概念、追踪原
- 【微服务】spring状态机模式使用详解
- Java实战:Netty+SpringBoot打造TCP长连接通讯方案
- 在 PostgreSQL 中,查看表是否被锁住以及解锁语句
- 掌握Go语言:Go语言类型转换,解锁高级用法,轻松驾驭复杂数据结构(3
- 【python】flask结合SQLAlchemy,在视图函数中实现对
- 【Linux实践室】Linux高级用户管理实战指南:创建与删除用户组操
- FlexLua:简化开发的LoRa无线氨气传感器技术
- 从零开始实现C++ TinyWebServer(九)---- 项目知识
- org.springframework.beans.factory.U
- Flink实战之 MySQL CDC
- mysql 内存缓冲池innodb
- Spring Boot集成百度UidGenerator雪花算法使用以及
- 篮球竞赛|基于Springboot的篮球竞赛预约平台系统设计与实现(源
- 【手写数据库toadb】虚拟文件描述符,连接表对象与物理文件的纽带,通
- 使用PySpider进行IP代理爬虫的技巧与实践
1.研究背景
计算受表面载荷影响的弹性体变形问题有着悠久的历史,涉及到许多著名的数学家和物理学家(Boussinesq 1885;Lamb 1901;Love 1911,1929;Shida 1912;Terazawa 1916;Munk & MacDonald 1960;Longman 1962,1963;Farrell 1972)。对于均匀弹性半空间的易于编码的解(Becker & Bevis 2004)在许多工程上是有用的,但在地球不是半空间也不均匀的地质应用中通常不适用。对于分层弹性半空间的解(例如Pan等人2007),其适用范围更广,但即使对于具有大孔径的载荷或在离载荷远处计算变形时,这种形式主义也不合适,这里所说的“大”是指距离地球半径的显著部分或更大的距离。因此,大多数地球物理应用的首选框架是分层、弹性、自引力球体和液态核心(Farrell 1972)。这个问题的解通常都是在涉及到载荷Love数的展开式中进行的,通常用符号(hn,kn,ln)来表示。通常,这些处理采用点载荷或圆盘载荷。
点载荷形式主义在接近标称点载荷时通常无效,从这个意义上讲,圆盘载荷形式主义更灵活。我们注意到,Love数形式主义适用于球对称弹性地球模型;横向各向同性可以被纳入这类模型,只要它符合球对称性(Pan等人2015)。弹性各向异性的一般类(例如横向变化的各向异性和方位各向异性)打破了球对称性,在这种情况下,Love数方法就不再适用,需要使用不同的方法,例如自引力有限元模型(虽然它们也存在自己的计算困难)。使用本文中提出的方程和代码的人隐含地假设弹性各向异性要么不存在,要么是一种非常特殊的类型。
在1975年至2000年期间,关于表面载荷问题的地球物理文献大多集中在冰盖地壳回弹调整方面,这涉及到粘弹性地球的载荷响应(Haskell 1935;Cathles 1975;Peltier & Andrews 1976;Wu & Peltier 1982)。几乎所有这些研究都使用了Love数形式主义。载荷问题的线性弹性和线性粘弹性版本通过弹性-粘弹性对应原理相互联系(Alfrey 1944;Read 1950;Lee 1950)。但是,从2001年开始,人们对纯弹性问题的兴趣出现了重大回升。这是因为(i)大地测量学家和地球物理学家开始意识到全球定位系统(GPS)接收机网络,以及更近期的全球导航卫星系统(GNSS)接收机,正在记录由水、雪和冰固体地球上的载荷所引起的季节性、持续性(即渐进性)和瞬时的弹性位移(Blewitt等人2001;Heki 2001;Mangiarotti等人2001;Dong等人2002;Bevis等人2005),而且在较小程度上还受大气压力变化的影响(Vandam等人1994),以及(ii)地球弹性变形的大地测量观测可以用于监测冰体质量(Khan等人2010;Bevis等人2012;Nielsen等人2012;Spada等人2012;Nielsen等人2013)和陆地水储存(Bevis等人2004,2005;Steckler等人2010;Fu等人2013;Borsa等人2014)的变化,从而提供了一种研究气候循环和气候变化的新方法。
描述分布式负荷或负荷变化的最简单方法是将其表示为一个或多个圆盘载荷。如果将质量或质量变化场表示为网格,则每个网格单元都可以视为圆盘载荷,或者,如果它位于地球测量站的远场,也可以视为点载荷。点载荷的响应可以与小而远的圆盘载荷的相似,除了在接近点载荷的地方,点载荷概念本身几乎从来不是现实的。本文的目的是两方面的。首先,我们希望向非专家提供有关如何计算地球对圆盘载荷的弹性响应的简单但完整的讨论。我们提供了一个MATLAB函数(diskload)来实现这个算法。我们的代码,像几乎所有它的同类一样,都会求和由载荷Love数和勒让德多项式或勒让德多项式的导数组成的项,其阶数为n = 0、1、2,...nmax。选择适当的nmax值非常重要,特别是当我们寻求对载荷的近场响应的准确估计时。当建模地球测量站位于质量损失正在使用非常高分辨率数字高程模型(DEM)进行表征的冰盖边缘附近时,由于DEM的网格间距或单元大小,适当的nmax值会按比例增加,所以这个错误相当容易发生。我们希望这个讨论能帮助我们的读者更自信地使用更一般和更复杂的软件包,例如REAR(Melini等人2015a,b)。(翻译自Bevis et al., 2016)
2.基本原理
所谓的“圆盘载荷”是一种特定类型的表面质量密度分布,其特点是(i)均匀施加的压力,即恒定的载荷“厚度”,和(ii)轴对称,这两个特点使得圆盘载荷在与冰盖等高度调整相关的应用中非常方便(例如Spada等人2012;Melini等人2015b),因为它可以直接展开成一系列球谐函数。此处略去基本理论公式的推导,感兴趣的参考原文。
引用至Bevis et al.(2016)
水平和垂直位移计算公式:
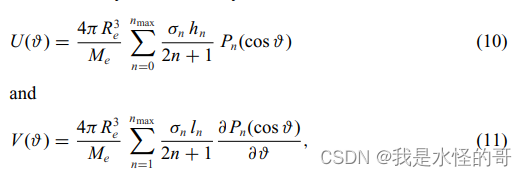
3.matlab程序
下载地址:
https://github.com/danielemelini/diskload
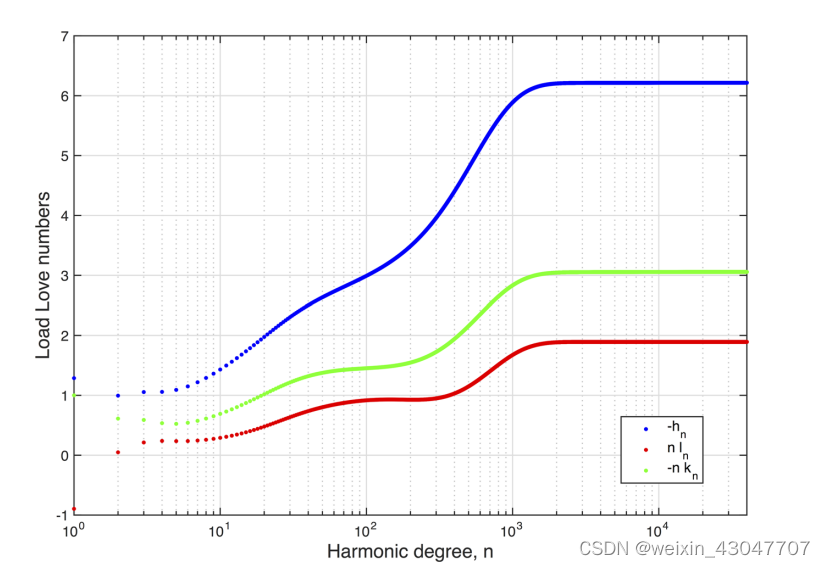
diskload MATLAB函数用于计算对施加在给定角半径和高度的圆盘上的均匀表面压力载荷的响应。弹性响应是在地球表面上的一个或多个点上计算的,这些点与圆盘载荷的中心指定的角距离相隔。弹性响应是使用用户提供的弹性负载Love数(h,k,l)计算的,这些Love数是使用特定的地球弹性结构模型生成的。下图是h l k负荷love数随阶数的变化示意图。
下载程序,在matlab中打开:
clear
%% Load LNs
load REF_6371_loading_love_numbers
%% Set some constants
alpha = 0.1; % Disk radius (degrees)
theta = linspace(0,alpha*5,100); % Range of colatitudes wrt disk center
Tw = 1; % Disk height (equivalent water height, m)
nmin = 0; % Minimum degree
nmax = [100:100:40000]; % Range of maximum degrees
imass = 1; % choose imass,0 or 1 (uncompensated/compensated load)
%%
if imass==1
fprintf('invoking a globally compensated load (icomp=1)\n')
else
fprintf('invoking an uncompensated load (icomp=0)\n')
end
% Compute the disc response for the maximum value of nmax
[U,V,G]= diskload(alpha,imass,theta,Tw,nmin,nmax(end),h_love,k_love,l_love);
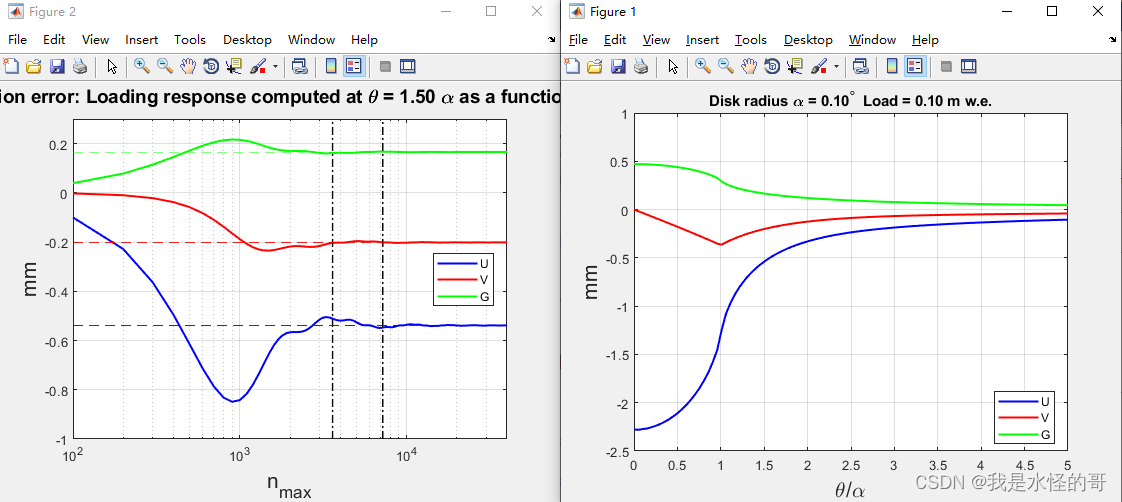
%% FIG 1
figure(1); clf;
plot( theta./alpha, U, 'b', 'LineWidth', 1.5 ); hold on;
plot( theta./alpha, V, 'r', 'LineWidth', 1.5 );
plot( theta./alpha, G, 'g', 'LineWidth', 1.5 );
xlabel( '\theta/\alpha', 'FontSize', 16 );
ylabel( 'mm', 'FontSize', 16 );
xlim([0 5]);
ylim([-2.5 1]);
grid on;
legend( 'U', 'V', 'G', 'Location', 'best' );
tit1=['Disk radius \alpha = ',sprintf('%4.2f^\\circ',alpha)];
tit2=[' Load = ',sprintf('%4.2f',alpha),' m w.e.'];
title([tit1 tit2])
%% Examine sensitivity to nmax
% Compute the disc response vs nmax at theta = K * alpha
K=1.5;
[U,V,G]= diskload(alpha,imass,K*alpha,Tw,nmin,nmax,h_love,k_love,l_love);
%% FIG 2
figure(2); clf;
semilogx( nmax, U, 'b', 'LineWidth', 1.5 ); hold on;
semilogx( nmax, V, 'r', 'LineWidth', 1.5 );
semilogx( nmax, G, 'g', 'LineWidth', 1.5 );
xlabel( 'n_{max}', 'FontSize', 16 );
ylabel( 'mm', 'FontSize', 16 );
xlim( [100 40000] );
ylim( [-1 .3] ); % good for K=1.5 or 1.25
%ylim( [-0.6 .2] ); % good for K = 1.75 or 2
nROT = 360 / alpha;
semilogx( [nROT nROT], ylim, 'k-.', 'LineWidth', 1.1 );
semilogx( 2*[nROT nROT], ylim, 'k-.', 'LineWidth', 1.1 );
semilogx(xlim,U(end)*[1 1],'b--', 'LineWidth', 0.5 );
semilogx(xlim,V(end)*[1 1],'r--', 'LineWidth', 0.5 );
semilogx(xlim,G(end)*[1 1],'g--', 'LineWidth', 0.5 );
hold off;
grid on;
legend( 'U', 'V', 'G', 'Location', 'best' );
Ht=title(['Truncation error: Loading response computed',...
' at \theta = ',sprintf('%4.2f',K),...
' \alpha as a function of n_{max} ']);
set(Ht,'FontSize',14)
运行结果:
关于负荷变形计算的问题,可以参见以下的文章:
利用GRACE和地表质量模型计算地球弹性负荷变形实验笔记_如何通过grace数据导出位移-CSDN博客
LoadDef python工具包学习二:利用JPL mascon数据计算地表站点的三维变形(E、N、V)_loaddef grace]-CSDN博客
参考文献:
Bevis, M., Melini, D., & Spada, G. (2016). On computing the geoelastic response to a disk load. Geophysical Journal International, 205(3), 1804-1812.
♥欢迎点赞收藏♥














