目录

144. 二叉树的前序遍历 Binary-tree Preorder Traversal  🌟

145. 二叉树的前序遍历 Binary-tree Postorder Traversal  🌟

对比： 94. 二叉树的中序遍历 Binary-tree Inorder Traversal  🌟

146. LRU缓存 LRU Cache  🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

二叉树专题（9）第146题除外

144. 二叉树的前序遍历 Binary-tree Preorder Traversal

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

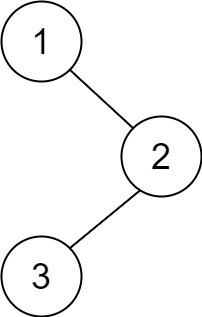
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

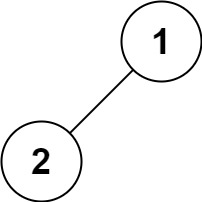
输入：root = [1,2]
输出：[1,2]

示例 5：

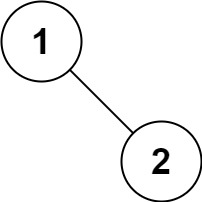
输入：root = [1,null,2]
输出：[1,2]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100 

  进阶：递归算法很简单，你可以通过迭代算法完成吗？

  公用的示例二叉树：

      3
     / \
    9  20
      /  \
     15   7
  

  遍历结果：

  前序遍历 preorder  = [3,9,20,15,7]
  中序遍历 inorder   = [9,3,15,20,7]
  后序遍历 postorder = [9,15,7,20,3]
  

   代码1： 递归

  package main
  import (
  	"fmt"
  )
  const null = -1 << 31
  type TreeNode struct {
  	Val   int
  	Left  *TreeNode
  	Right *TreeNode
  }
  func preorderTraversal(root *TreeNode) []int {
  	var res []int
  	preorder(root, &res)
  	return res
  }
  func preorder(root *TreeNode, res *[]int) {
  	if root == nil {
  		return
  	}
  	*res = append(*res, root.Val)
  	preorder(root.Left, res)
  	preorder(root.Right, res)
  }
  func buildTree(nums []int) *TreeNode {
  	if len(nums) == 0 {
  		return nil
  	}
  	root := &TreeNode{Val: nums[0]}
  	Queue := []*TreeNode{root}
  	idx := 1
  	for idx < len(nums) {
  		node := Queue[0]
  		Queue = Queue[1:]
  		if nums[idx] != null {
  			node.Left = &TreeNode{Val: nums[idx]}
  			Queue = append(Queue, node.Left)
  		}
  		idx++
  		if idx < len(nums) && nums[idx] != null {
  			node.Right = &TreeNode{Val: nums[idx]}
  			Queue = append(Queue, node.Right)
  		}
  		idx++
  	}
  	return root
  }
  func ArrayToString(arr []int) string {
  	res := "["
  	for i := 0; i < len(arr); i++ {
  		res += fmt.Sprint(arr[i])
  		if i != len(arr)-1 {
  			res += ","
  		}
  	}
  	return res + "]"
  }
  func main() {
  	nums := []int{1, null, 2, 3}
  	root := buildTree(nums)
  	fmt.Println(ArrayToString(preorderTraversal(root)))
  	nums = []int{3, 9, 20, null, null, 15, 7}
  	root = buildTree(nums)
  	fmt.Println(ArrayToString(preorderTraversal(root)))
  }
  

   代码2： 迭代

  package main
  import (
  	"fmt"
  )
  const null = -1 << 31
  type TreeNode struct {
  	Val   int
  	Left  *TreeNode
  	Right *TreeNode
  }
  func preorderTraversal(root *TreeNode) []int {
  	var res []int
  	if root == nil {
  		return res
  	}
  	stack := []*TreeNode{}
  	stack = append(stack, root)
  	for len(stack) > 0 {
  		cur := stack[len(stack)-1]
  		stack = stack[:len(stack)-1]
  		res = append(res, cur.Val)
  		if cur.Right != nil {
  			stack = append(stack, cur.Right)
  		}
  		if cur.Left != nil {
  			stack = append(stack, cur.Left)
  		}
  	}
  	return res
  }
  func buildTree(nums []int) *TreeNode {
  	if len(nums) == 0 {
  		return nil
  	}
  	root := &TreeNode{Val: nums[0]}
  	Queue := []*TreeNode{root}
  	idx := 1
  	for idx < len(nums) {
  		node := Queue[0]
  		Queue = Queue[1:]
  		if nums[idx] != null {
  			node.Left = &TreeNode{Val: nums[idx]}
  			Queue = append(Queue, node.Left)
  		}
  		idx++
  		if idx < len(nums) && nums[idx] != null {
  			node.Right = &TreeNode{Val: nums[idx]}
  			Queue = append(Queue, node.Right)
  		}
  		idx++
  	}
  	return root
  }
  func ArrayToString(arr []int) string {
  	res := "["
  	for i := 0; i < len(arr); i++ {
  		res += fmt.Sprint(arr[i])
  		if i != len(arr)-1 {
  			res += ","
  		}
  	}
  	return res + "]"
  }
  func main() {
  	nums := []int{1, null, 2, 3}
  	root := buildTree(nums)
  	fmt.Println(ArrayToString(preorderTraversal(root)))
  	nums = []int{3, 9, 20, null, null, 15, 7}
  	root = buildTree(nums)
  	fmt.Println(ArrayToString(preorderTraversal(root)))
  }
  

  输出：

  [1,2,3]

  [3,9,20,15,7]

  ---

  145. 二叉树的后序遍历 Binary-tree Postorder Traversal

  给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

  示例 1：

  

  输入：root = [1,null,2,3]
  输出：[3,2,1]
  

  示例 2：

  输入：root = []
  输出：[]
  

  示例 3：

  输入：root = [1]
  输出：[1]
  

  提示：

  • 树中节点的数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

    进阶：递归算法很简单，你可以通过迭代算法完成吗？

     代码1： 递归

    package main
    import (
    	"fmt"
    )
    const null = -1 << 31
    type TreeNode struct {
    	Val   int
    	Left  *TreeNode
    	Right *TreeNode
    }
    func postorderTraversal(root *TreeNode) []int {
    	var res []int
    	postorder(root, &res)
    	return res
    }
    func postorder(root *TreeNode, res *[]int) {
    	if root == nil {
    		return
    	}
    	postorder(root.Left, res)
    	postorder(root.Right, res)
    	*res = append(*res, root.Val)
    }
    func buildTree(nums []int) *TreeNode {
    	if len(nums) == 0 {
    		return nil
    	}
    	root := &TreeNode{Val: nums[0]}
    	Queue := []*TreeNode{root}
    	idx := 1
    	for idx < len(nums) {
    		node := Queue[0]
    		Queue = Queue[1:]
    		if nums[idx] != null {
    			node.Left = &TreeNode{Val: nums[idx]}
    			Queue = append(Queue, node.Left)
    		}
    		idx++
    		if idx < len(nums) && nums[idx] != null {
    			node.Right = &TreeNode{Val: nums[idx]}
    			Queue = append(Queue, node.Right)
    		}
    		idx++
    	}
    	return root
    }
    func ArrayToString(arr []int) string {
    	res := "["
    	for i := 0; i < len(arr); i++ {
    		res += fmt.Sprint(arr[i])
    		if i != len(arr)-1 {
    			res += ","
    		}
    	}
    	return res + "]"
    }
    func main() {
    	nums := []int{1, null, 2, 3}
    	root := buildTree(nums)
    	fmt.Println(ArrayToString(postorderTraversal(root)))
    	nums = []int{3, 9, 20, null, null, 15, 7}
    	root = buildTree(nums)
    	fmt.Println(ArrayToString(postorderTraversal(root)))
    }
    

     代码2： 迭代

    package main
    import (
    	"fmt"
    )
    const null = -1 << 31
    type TreeNode struct {
    	Val   int
    	Left  *TreeNode
    	Right *TreeNode
    }
    func postorderTraversal(root *TreeNode) []int {
    	var res []int
    	if root == nil {
    		return res
    	}
    	stack := []*TreeNode{}
    	stack = append(stack, root)
    	for len(stack) > 0 {
    		cur := stack[len(stack)-1]
    		stack = stack[:len(stack)-1]
    		res = append([]int{cur.Val}, res...)
    		if cur.Left != nil {
    			stack = append(stack, cur.Left)
    		}
    		if cur.Right != nil {
    			stack = append(stack, cur.Right)
    		}
    	}
    	return res
    }
    func buildTree(nums []int) *TreeNode {
    	if len(nums) == 0 {
    		return nil
    	}
    	root := &TreeNode{Val: nums[0]}
    	Queue := []*TreeNode{root}
    	idx := 1
    	for idx < len(nums) {
    		node := Queue[0]
    		Queue = Queue[1:]
    		if nums[idx] != null {
    			node.Left = &TreeNode{Val: nums[idx]}
    			Queue = append(Queue, node.Left)
    		}
    		idx++
    		if idx < len(nums) && nums[idx] != null {
    			node.Right = &TreeNode{Val: nums[idx]}
    			Queue = append(Queue, node.Right)
    		}
    		idx++
    	}
    	return root
    }
    func ArrayToString(arr []int) string {
    	res := "["
    	for i := 0; i < len(arr); i++ {
    		res += fmt.Sprint(arr[i])
    		if i != len(arr)-1 {
    			res += ","
    		}
    	}
    	return res + "]"
    }
    func main() {
    	nums := []int{1, null, 2, 3}
    	root := buildTree(nums)
    	fmt.Println(ArrayToString(postorderTraversal(root)))
    	nums = []int{3, 9, 20, null, null, 15, 7}
    	root = buildTree(nums)
    	fmt.Println(ArrayToString(postorderTraversal(root)))
    }
    

    输出：

    [3,2,1]

    [9,15,7,20,3]

    ---

    对比： 94. 二叉树的中序遍历 Binary-tree Inorder Traversal

    给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

    示例 1：

    

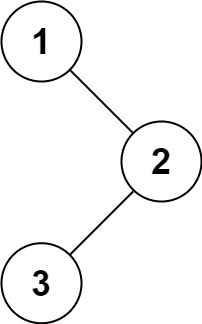
    输入：root = [1,null,2,3]
    输出：[1,3,2]
    

    示例 2：

    输入：root = []
    输出：[]
    

    示例 3：

    输入：root = [1]
    输出：[1]
    

    提示：

    • 树中节点数目在范围 [0, 100] 内
    • -100 <= Node.val <= 100

      进阶: 递归算法很简单，你可以通过迭代算法完成吗？

      代码1： 递归法

      package main
      import (
      	"fmt"
      )
      const null = -1 << 31
      type TreeNode struct {
      	Val   int
      	Left  *TreeNode
      	Right *TreeNode
      }
      func inorderTraversal(root *TreeNode) []int {
      	var res []int
      	inorder(root, &res)
      	return res
      }
      func inorder(root *TreeNode, res *[]int) {
      	if root == nil {
      		return
      	}
      	inorder(root.Left, res)
      	*res = append(*res, root.Val)
      	inorder(root.Right, res)
      }
      func buildTree(nums []int) *TreeNode {
      	if len(nums) == 0 {
      		return nil
      	}
      	root := &TreeNode{Val: nums[0]}
      	Queue := []*TreeNode{root}
      	idx := 1
      	for idx < len(nums) {
      		node := Queue[0]
      		Queue = Queue[1:]
      		if nums[idx] != null {
      			node.Left = &TreeNode{Val: nums[idx]}
      			Queue = append(Queue, node.Left)
      		}
      		idx++
      		if idx < len(nums) && nums[idx] != null {
      			node.Right = &TreeNode{Val: nums[idx]}
      			Queue = append(Queue, node.Right)
      		}
      		idx++
      	}
      	return root
      }
      func ArrayToString(arr []int) string {
      	res := "["
      	for i := 0; i < len(arr); i++ {
      		res += fmt.Sprint(arr[i])
      		if i != len(arr)-1 {
      			res += ","
      		}
      	}
      	return res + "]"
      }
      func main() {
      	nums := []int{1, null, 2, 3}
      	root := buildTree(nums)
      	fmt.Println(ArrayToString(inorderTraversal(root)))
      	nums = []int{3, 9, 20, null, null, 15, 7}
      	root = buildTree(nums)
      	fmt.Println(ArrayToString(inorderTraversal(root)))
      }
      

      代码2： 迭代法

      package main
      import (
      	"fmt"
      )
      const null = -1 << 31
      type TreeNode struct {
      	Val   int
      	Left  *TreeNode
      	Right *TreeNode
      }
      func inorderTraversal(root *TreeNode) []int {
      	var res []int
      	stack := []*TreeNode{}
      	cur := root
      	for cur != nil || len(stack) > 0 {
      		for cur != nil {
      			stack = append(stack, cur)
      			cur = cur.Left
      		}
      		cur = stack[len(stack)-1]
      		stack = stack[:len(stack)-1]
      		res = append(res, cur.Val)
      		cur = cur.Right
      	}
      	return res
      }
      func buildTree(nums []int) *TreeNode {
      	if len(nums) == 0 {
      		return nil
      	}
      	root := &TreeNode{Val: nums[0]}
      	Queue := []*TreeNode{root}
      	idx := 1
      	for idx < len(nums) {
      		node := Queue[0]
      		Queue = Queue[1:]
      		if nums[idx] != null {
      			node.Left = &TreeNode{Val: nums[idx]}
      			Queue = append(Queue, node.Left)
      		}
      		idx++
      		if idx < len(nums) && nums[idx] != null {
      			node.Right = &TreeNode{Val: nums[idx]}
      			Queue = append(Queue, node.Right)
      		}
      		idx++
      	}
      	return root
      }
      func ArrayToString(arr []int) string {
      	res := "["
      	for i := 0; i < len(arr); i++ {
      		res += fmt.Sprint(arr[i])
      		if i != len(arr)-1 {
      			res += ","
      		}
      	}
      	return res + "]"
      }
      func main() {
      	nums := []int{1, null, 2, 3}
      	root := buildTree(nums)
      	fmt.Println(ArrayToString(inorderTraversal(root)))
      	nums = []int{3, 9, 20, null, null, 15, 7}
      	root = buildTree(nums)
      	fmt.Println(ArrayToString(inorderTraversal(root)))
      }
      

      输出：

      [1,3,2]
      [9,3,15,20,7]

      ---

      三种遍历的递归对比

      “根左右、左根右、左右根”

      func preorder(root *TreeNode, res *[]int) {
      	*res = append(*res, root.Val)
      	preorder(root.Left, res)
      	preorder(root.Right, res)
      }
      func inorder(root *TreeNode, res *[]int) {
      	inorder(root.Left, res)
      	*res = append(*res, root.Val)
      	inorder(root.Right, res)
      }
      func postorder(root *TreeNode, res *[]int) {
      	postorder(root.Left, res)
      	postorder(root.Right, res)
      	*res = append(*res, root.Val)
      }

      三种遍历的迭代对比

      注意左、右子节点的压栈顺序，以及后序结果中的“追加”实为“前插”

      func preorderTraversal(root *TreeNode) []int {
          var res []int
          if root == nil {
              return res
          }
          stack := []*TreeNode{}
          stack = append(stack, root)
          for len(stack) > 0 {
              cur := stack[len(stack)-1]
              stack = stack[:len(stack)-1]
              res = append(res, cur.Val)
              if cur.Right != nil {
                  stack = append(stack, cur.Right)
              }
              if cur.Left != nil {
                  stack = append(stack, cur.Left)
              }
          }
          return res
      }
      func inorderTraversal(root *TreeNode) []int {
          var res []int
          stack := []*TreeNode{}
          cur := root
          for cur != nil || len(stack) > 0 {
              for cur != nil {
                  stack = append(stack, cur)
                  cur = cur.Left
              }
              cur = stack[len(stack)-1]
              stack = stack[:len(stack)-1]
              res = append(res, cur.Val)
              cur = cur.Right
          }
          return res
      }
      func postorderTraversal(root *Treecur) []int {
          var res []int
          if root == nil {
              return res
          }
          stack := []*Treecur{}
          stack = append(stack, root)
          for len(stack) > 0 {
              cur := stack[len(stack)-1]
              stack = stack[:len(stack)-1]
              res = append([]int{cur.Val}, res...)
              if cur.Left != nil {
                  stack = append(stack, cur.Left)
              }
              if cur.Right != nil {
                  stack = append(stack, cur.Right)
              }
          }
          return res
      }
      

      ---

      146. LRU缓存 LRU Cache

      请你设计并实现一个满足​ LRU (最近最少使用) 缓存 ​约束的数据结构。

      实现 LRUCache 类：

      • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
      • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
      • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

        函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

        示例：

        输入
        ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
        [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
        输出
        [null, null, null, 1, null, -1, null, -1, 3, 4]
        解释
        LRUCache lRUCache = new LRUCache(2);
        lRUCache.put(1, 1); // 缓存是 {1=1}
        lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
        lRUCache.get(1);    // 返回 1
        lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
        lRUCache.get(2);    // 返回 -1 (未找到)
        lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
        lRUCache.get(1);    // 返回 -1 (未找到)
        lRUCache.get(3);    // 返回 3
        lRUCache.get(4);    // 返回 4
        

        提示：

        • 1 <= capacity <= 3000
        • 0 <= key <= 10000
        • 0 <= value <= 10^5
        • 最多调用 2 * 10^5 次 get 和 put

           代码：

          type LRUCache struct {
              capacity int
              cache    map[int]*list.Element
              list     *list.List
          }
          type pair struct {
              key   int
              value int
          }
          func Constructor(capacity int) LRUCache {
              return LRUCache{
                  capacity: capacity,
                  cache:    make(map[int]*list.Element),
                  list:     list.New(),
              }
          }
          func (c *LRUCache) Get(key int) int {
              if elem, ok := c.cache[key]; ok {
                  c.list.MoveToFront(elem)
                  return elem.Value.(*pair).value
              }
              return -1
          }
          func (c *LRUCache) Put(key int, value int) {
              if elem, ok := c.cache[key]; ok {
                  elem.Value.(*pair).value = value
                  c.list.MoveToFront(elem)
              } else {
                  if c.list.Len() == c.capacity {
                      // remove the least recently used element
                      tailElem := c.list.Back()
                      delete(c.cache, tailElem.Value.(*pair).key)
                      c.list.Remove(tailElem)
                  }
                  // insert new element to front
                  newElem := c.list.PushFront(&pair{key, value})
                  c.cache[key] = newElem
              }
          }
          

          输出：

          略

          ---

          🌟 每日一练刷题专栏 🌟

          ✨ 持续，努力奋斗做强刷题搬运工！

          👍 点赞，你的认可是我坚持的动力！ 

          🌟 收藏，你的青睐是我努力的方向！ 

          ✎ 评论，你的意见是我进步的财富！  

          ☸ 主页：https://hannyang.blog.csdn.net/ 

          	Golang每日一练 专栏
          	Python每日一练 专栏
          	C/C++每日一练 专栏
          	Java每日一练 专栏

           
           深圳做网站多少钱  番禺网站建设公司  搭建网络  注册公司需要的资料  服装设计  博兴网站制作