【问题引入】

在许多领域的研究与应用中，往往需要对反映事物的多个变量进行大量的观测，收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息，但也在一定程度上增加了数据采集的工作量，更重要的是在多数情况下，许多变量之间可能存在相关性，从而增加了问题分析的复杂性，同时对分析带来不便。如果分别对每个指标进行分析，分析往往是孤立的，而不是综合的。盲目减少指标会损失很多信息，容易产生错误的结论。因此需要找到一个合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系，因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析与因子分析就属于这类降维的方法。

【PCA原理】PCA即主成分分析，是用一个超平面对所有样本进行恰当表达的方法，思想是将n维特征映射到k维上（k

【PCA算法步骤】

1. 去平均值(即去中心化)，即每一位特征减去各自的平均值。
2. 计算协方差矩阵，C = (X' * X) / (N-1)

   注：这里除或不除样本数量N或N-1,其实对求出的特征向量没有影响。

3. 求协方差矩阵的特征值与特征向量。
4. 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
5. 将数据转换到k个特征向量构建的新空间中，即Y=PX。

【性质】

1. 缓解维度灾难：PCA 算法通过舍去一部分信息之后能使得样本的采样密度增大（因为维数降低了），这是缓解维度灾难的重要手段；
2. 降噪：当数据受到噪声影响时，最小特征值对应的特征向量往往与噪声有关，将它们舍弃能在一定程度上起到降噪的效果；
3. 过拟合：PCA 保留了主要信息，但这个主要信息只是针对训练集的，而且这个主要信息未必是重要信息。有可能舍弃了一些看似无用的信息，但是这些看似无用的信息恰好是重要信息，只是在训练集上没有很大的表现，所以 PCA 也可能加剧了过拟合；
4. 特征独立：PCA 不仅将数据压缩到低维，它也使得降维之后的数据各特征相互独立；

【主程序代码】

%%
clear all;
close all;
% 生成一些样本数据
N = 100; % 样本数量
D = 2; % 数据维度
X = randn(N,D)*0.5 + repmat([2, 3], N, 1); % 生成高斯分布的数据
% 中心化数据
mu = mean(X);
X = X - repmat(mu, size(X,1), 1);
% 计算协方差矩阵
C = (X' * X) / (N-1);
% 计算特征向量和特征值
[V, D] = eig(C);
% 将特征向量按特征值从大到小排序
[~, I] = sort(diag(D), 'descend');
V = V(:,I);
% 选取前k个特征向量
k = 1;
W = V(:,1:k);
% 将数据投影到新的空间中
Y = X*W;
% 可视化结果
figure;
scatter(X(:,1), X(:,2), 'filled', 'MarkerFaceColor', 'b');
hold on;
quiver(mu(1), mu(2), W(1), W(2), 'r', 'LineWidth', 2);
xlabel('X1');
ylabel('X2');
title('Principal Component Analysis (PCA)');

【程序分析】

1. 生成样本数据：通过使用 randn 函数生成 N 个二维高斯分布的样本数据，然后加上一个偏置项 [2, 3]，并存储在名为 X 的矩阵中。
2. 中心化数据：计算数据的均值 mu，然后使用 repmat 函数将其复制成与 X 大小相同的矩阵，并将其从 X 中减去，实现数据的中心化。
3. 计算协方差矩阵：使用公式 C = (X’ * X) / (N-1) 计算数据的协方差矩阵 C，其中 X’ 表示 X 的转置。
4. 计算特征向量和特征值：使用 eig 函数计算协方差矩阵 C 的特征向量 V 和特征值 D。
5. 特征向量排序：使用 sort 函数和 diag 函数将特征向量 V 按照特征值 D 的从大到小的顺序进行排序，并存储在 V 中。
6. 选择主成分：在这个例子中，我们选择第一个主成分，即特征值最大的特征向量，将其存储在名为 W 的矩阵中。
7. 将数据投影到新的空间中：将中心化的数据 X 与选定的主成分 W 相乘，得到投影后的数据 Y。
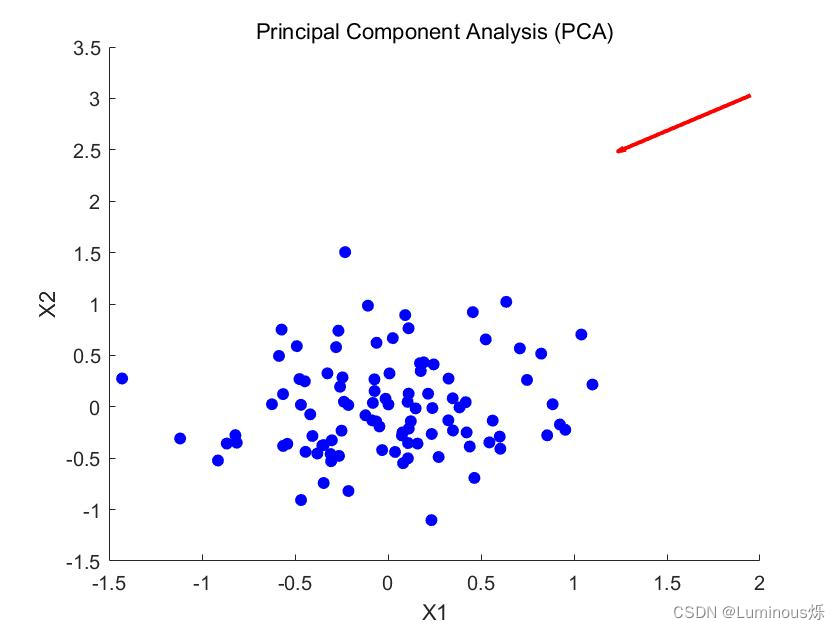
8. 可视化结果：使用 scatter 函数绘制原始数据的散点图，并使用 quiver 函数绘制原始数据的均值 mu 和选定的主成分 W 的方向。

这个程序演示了如何使用主成分分析（PCA）对二维数据进行降维，并将数据投影到新的一维空间中。

【运行结果】

喜欢我就关注我吧！！！！